Высшая математика

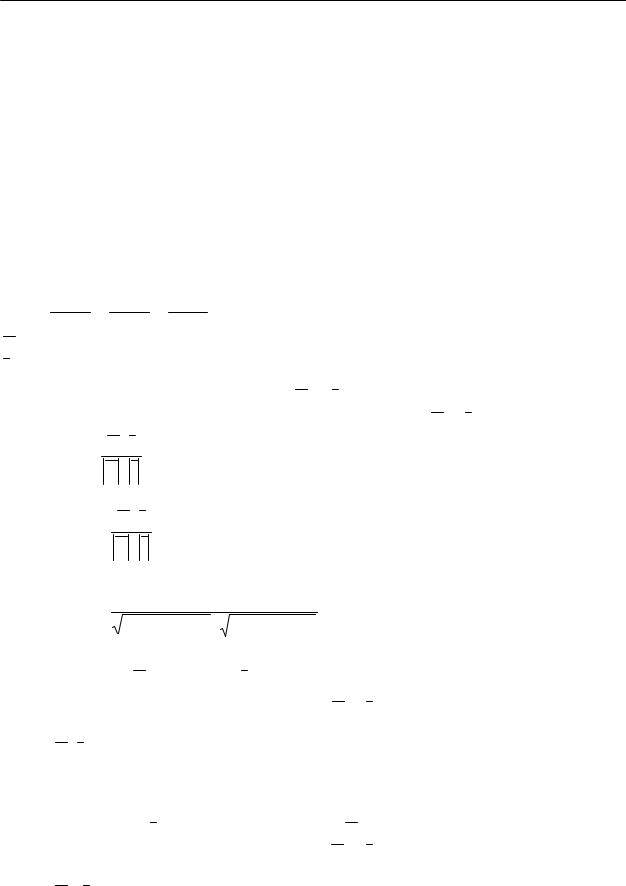
Формулы (2) и (3) являются формулами для определения угла между двумя прямыми в пространстве.

4) Условия параллельности и перпендикулярности двух прямых в пространстве.

Для того, чтобы две прямые были параллельны, необходимо и достаточно, чтобы их направляющие векторы l1 и l 2 были коллинеарны, т.е. соответствующие координаты

Условие (4) является условием параллельности двух прямых в пространстве.

Для того, чтобы прямые были перпендикулярны между собой, необходимо и достаточно, чтобы направляющие их векторы l1 и l 2 были ортогональными.

Условие ортогональности двух векторов l1 и l 2 :

является условием перпендикулярности двух прямых в пространстве.

Пример. Найти уравнение прямой, проходящей через точку М(3; 2; -1) перпендикулярно двум прямым:

Составим уравнение любой прямой, проходящей через точку М:

Используя условие перпендикулярности искомой прямой к прямой а1, а затем к прямой а2 получим

2m-3n+5p=0 4m+n-2p=0

61

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Из этой однородной структуры линейных уравнений с неизвестными m, n, p найдем отношения неизвестных:

Подставляя в уравнения прямой (6) вместо m, n, p пропорциональные им величины, получим искомые уравнения:

5) Углом между прямой и плоскостью называют любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Пусть дано уравнение плоскости П:

Ax+By+Cz+D=0

и уравнение прямой l :

x −mx 0 = y −ny 0 = z −pz0

N ={А; В; С}- нормальный вектор плоскости

l ={m; n; p} – направляющий вектор прямой

Обозначим угол между векторами N и l через ϕ, а угол между плоскостью П и прямой l – через α. Найдем косинус угла ϕ между векторами N и l :

cosϕ = (N l ) N l

При этом sinα=±cosϕ. Следовательно,

sin α = ±(N l ) N l

или, в координатной форме,

Для того, чтобы плоскость П была параллельна прямой l необходимо и достаточ-

но, чтобы векторы N ={А; В; С} и l ={m; n; p} были ортогональны между собой.

Условие ортогональности двух векторов N и l может быть записано как равенство нулю их скалярного произведения:

( N l )=0

или в координатной форме: Am+Bn+Cp=0

Длятого, чтобы прямая l былаперпендикулярна плоскости П, необходимо и доста-

точно, чтобы вектор l был коллинеарен вектору N .

Условие коллинеарности двух векторов N и l может быть записано как равенство нулю их векторного произведения:

( N l )=0

62

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

или

mA = Bn = Cp

Пример. Составить уравнение плоскости П, проходящей через точку М(-1; 2; -3) параллельно двум прямым:

Используем условие параллельности плоскости П и прямой l 1 , а затем к прямой

l 2 :

3А+4В+5С=0

2А-3В+С=0

Из этой системы однородных уравнений определим отношения коэффициентов А, В, С и затем в уравнение (4) вместо коэффициентов А, В, С подставим пропорциональные им величины:

11(x+1)+13(y-2)+17(z+3)=0; 11x+13y+17z+36=0.

6) Пучок плоскостей.

Через всякую прямую в пространстве можно провести бесчисленное множество плоскостей. Совокупность всех плоскостей, проходящих через одну и ту же прямую, на-

зывается пучком плоскостей.

где λ – произвольное число. При любом λ это уравнение первой степени, кроме того, при любом λ это уравнение определяет плоскость, проходящую через прямую (1).

Действительно, если точка М0 принадлежит прямой (1), то:

A1x0 + B1y0 + C1z0 + D1 = 0A 2x0 + B2 y0 + C2 z0 + D 2 = 0

и следовательно

A1x0+B1y0+C1z0+D1+λ(A2x0+B2y0+C2z0+D2)=0.

Уравнение (2) называется уравнением пучка плоскостей, проходящих через пря-

мую (1).

63

или

(2+λ)x+(5λ-3)y+(4-2λ)z+(3λ-1)=0

Определим λ, используя условие перпендикулярности плоскостей: 3(2+λ)-4(5λ- 3)+(4-2λ)=0. Откуда λ = 1922 . Подставив значение в уравнение (3), найдем уравнение проек-

тирующей плоскости:

2x −3y +4z −1+ 1922 (x +5y −2z +3) = 0 60x +53y +32z +47 = 0

Уравнения искомой проекции можно записать как уравнения линии пересечения плоскостей:

3x - 4y + z - 8 = 0

60x + 53y - 32z + 47 = 0

Преобразуем это уравнение: (3+λ)x+(2+4λ)y+(5+3λ)z+(6+4λ)=0. Используя условие параллельности прямой и плоскости получим: 3(3+λ)+2(2+4λ)-3(5+3λ)=0. Отсюда λ=1. Подставляя найденное значение λ в уравнение (*), найдем: 4x+6y+8z+10=0 или

2x+3y+4z+5=0.

Пример. Найти расстояние от точки М(1; 1; 1) до прямой x −211 = y −518 = z−−24

Решение. Проведем через М плоскость П, перпендикулярную к данной прямой и найдем точку Р, где эта плоскость пересекает данную прямую. Искомое расстояние от точки М до данной прямой будет равно расстоянию от точки М до точки Р.

Искомое уравнение плоскости П можно записать в виде: A(x-1) + B(y-1) + C(z-1)=0;

эта плоскость должна быть перпендикулярна к данной прямой. По условию перпендикулярности прямой к плоскости имеем:

64

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

А2 = В5 = −С2 .

Выбирая здесь множитель пропорциональности для простоты равным единице, находим А=2, В=5, С=-2. Итак, плоскость имеет уравнение 2(x-1)+5(y-1)-2(z-1)=0 или

2x+5y-2z=0.

Теперь мы должны найти точку Р, в которой эта плоскость пересекается с данной прямой. Для этого нужно уравнение данной прямой решить совместно с найденным уравнением плоскости П.

x −211 = y −518 = z−−24 = t

Отсюда x=2t+11, y=5t+18, z=4-2t. Подставляя эти уравнения в уравнение найденной плос-

кости 2x+5y-2z-5=0 получим:

4t + 22 + 25t + 90 + 4t – 8 - 5 = 0; 33t = -99;

t = -3.

Координаты точки Р будут равны x=5, y=3, z=10.

Искомое расстояние d от точки М до данной прямой, равное расстоянию между точками М и Р, найдется по формуле нахождения расстояния между двумя точками

М1М2 ={a2-a1; b2-b1; c2-c1} и направляющие векторы прямых l1 и l 2 компланарны в том и только в том случае, когда прямые l 1 и l 2 лежат в одной плоскости. Условием компланарности трех векторов является равенство нулю их смешанного произведения:

М1М2 l1 l 2 =0, что в координатной записи может быть представлено в следующем виде:

65

4.ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

4.Введение в математический анализ

4.1.Основные понятия о множествах, логическая символика

4.1.1. Некоторые сведения о множествах

Основные понятия

Множество – есть исходное, начальное (а следовательно, и неопределяемое) понятие. Можно лишь сказать, что множество есть собрание объектов, при этом не будем уточнять, какие собрания объектов являются множествами. Объекты этого собрания называются элементами множества.

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если множество состоит из n элементов, то это обозначают следующим образом:

A = {x1 , x2 ,..., xn } = {xn } .

Часто приходится сталкиваться с другими, неконечными, или, как принято говорить, бесконечными множествами. Таковы, например, множества всех натуральных чисел, всех нечетных чисел и т.д.

К числу конечных множеств мы будем относить и пустое множество, т.е. множество, не содержащее ни одного элемента; число элементов пустого множества есть нуль. Такое множество обозначим символом .

Если элемент x принадлежит множеству А, то пишут x A.

Запись x A , или x A означает, что x не есть элемент множества А.

Запись Α Β (или Β Α) означает, что каждый элемент множества А является элементом множества В или, другими словами, множество А есть подмножество множеств В (или множество А включено в множество В).

Два множества называются равными, если они состоят из одних и тех же элементов: запись А=В.

Если А есть подмножество В, причем множество А не совпадает с множеством В, то пишут Α Β или Β Α.

Если множество А не принадлежит множеству В, то пишут

Α Β, A B . Знаки , , , , называются знаками включения.

разберем некоторые понятия математической логики. Прежде всего, что такое математическая логика?

Математическая логиканаука о законах логического вывода.

В математической логике под предложением понимают то же самое, что вкладывают в смысл этого термина в грамматике любого естественного языка.

Высказыванием называется предложение, о котором имеет смысл говорить, что оно истинно или ложно. Каждое высказывание либо истинно, либо ложно. Истинному высказыванию будем ставить в соответствие единицу, а ложному - логический ноль (1;0).

Пример: (10=15)=0 (высказывание “10 равно 15” ложно) (5>-1)=1 (высказывание “5 больше -1” истинно).

Будем обозначать высказывания буквами какого-либо алфавита: X, Y,L,.........; А, В ,......

Высказывательная форма – это выражение, содержащее одну или несколько переменных и становящееся высказыванием при подстановке чисел или элементов каких-либо множеств вместо своих переменных.

66

4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Основные операции алгебры логики

При записи математических рассуждений будем использовать следующую экономную символику, описывающую различные алгебраические операции (операции алгебры логики).

а) Отрицание (негоция) : X; X -“не X”. Отрицанием высказывания X называется X или X (“не X” или “неверно, что X”), которое означает высказывание, утверждающее, что X ложно.

Таблица истинности

б) Коньюнкцией (логическим произведением) высказываний X, Y

называется высказывание X Y (“X и Y”), истинное тогда и только тогда, когда оба высказывания, X и Y, истинны.

в) Дизьюнкция (логическое сложение) высказываний X, Y- X Y (“X или Y”) – высказывание истинное тогда и только тогда, когда истинно хотя бы одно из высказываний

X и Y.

г) Импликация (логическое следствие) X Y (“если X, то Y “ или “из X следует, что Y”) есть высказывание, ложное тогда и только тогда, когда X истинно, Y ложно. В остальных случаях X Y истинно.

X Y означает: X является достаточным условием для Y. Y является необходимым условием для X.

Таблица истинности

д) Эквивалентность двух высказываний X и Y (“X тогда и только тогда, когда Y”) – есть высказывание X Y, истинное тогда и только тогда, когда оба высказывания X и Yсразу истинны или ложны.

X Y – “X” является необходимым и достаточным условием “Y”.

67

4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Таблица истинности.

Кванторы

Иногда удобно представить некоторые словесные выражения посредством символов.– каково бы ни было, для любого (квантор всеобщности).

– существует (квантор существования).

( x A):α -для любого x Α выполняется предложение α.

Символом “:” будем обозначать следующую группу слов: “такое, что”, “удовлетворяет условию”, выполняется”.

Отрицание высказываний, содержащих кванторы

Отрицание под знаком или превращает его, соответственно, в знак или и переносится на свойство, стоящее после двоеточия.

Пример 1.

Пусть имеем высказывание: ( x Α): x ≤ ξ (для любого x из множества А имеет место неравенство x ≤ ξ). Если высказываемое утверждение не имеет место, то следовательно, неравенство x ≤ ξ выполняется не для каждого x Α, значит существует элемент x Α, для которого неравенство x ≤ ξ не выполняется.

( x A): x ≤ ξ ( x A): x ≤ ξ ( x A): x > ξ

Пример 2.

Используя закон Моргана, построить отрицание предела функции f(x) в точке x=а. Сформулируем определение предела функции f(x) в точке x=a по Коши с использо-

ванием введенной символики

def { } [ ]

(lim f (x) = b) ≡( E > 0)( δ > 0) : ( x x ) 0 < x − a < δ f (x) −b < ε .

x→a

Здесь на языке алгебры записано: вещественное число a называется пределом функции f(x) в точке x=a, если для любого вещественного положительного числа E найдется вещественное положительное число δ, что для всех значений аргумента x из области определения таких, что, если выполнены неравенства 0 < x −a < δ , будет следовать нера-

венство f (x) − b < ε.

68

4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Операции над множествами Объединение А В множеств А и В

Множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из данных множеств, называется объединением множества А и В. Указанное определение легко распространяется на случай трех и более множеств

dtf

A B ≡{x :(x A) (x B)}

Пример 1.

А{1,2,3,4,5}, В{1,2}, А В={1,2,3,4,5}.

Множество А В по определению не содержит неразличимых элементов и, следовательно, элементы 1 и2, входящие в множества А и В, входят в А В один раз. Пересечение А∩В множеств А и В есть множество элементов, принадлежащих и А и В.

def

A ∩ B ≡{x : (x A) (x B)}

Пример 2.

А{1,2,3,4,5}; В{1,2} А∩В={1,2}

Два множества А и В называются непересекающимися, если А∩В=0.

Разность А\В множеств А и В

Разностью множеств А и В называется совокупность тех элементов А, которые не содержатся в В.

Пример 3.

А={1,2,3,4,5}, В={1,2} А\В={3,4,5}.

Взаимно однозначное соответствие и эквивалентность множеств

Если каждому элементу множества А сопоставлен единственный элемент множества В и при этом всякий элемент множества В сопоставляется одному и только одному элементу множества А, то говорят, что между множествами А и В установлено взаимно однозначное соответствие.

69

4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Множества, между которыми установлено взаимно однозначное соответствие, называются эквивалентными. Это записывается следующим образом : А~В. Eсли два множества эквивалентны, то говорят, что они равномощны, или имеют одну и ту же мощность.

Прямое произведение двух множеств

Пусть имеются два множества А и В и пусть а А, b B. Совокупность всевозможных упорядоченных пар (а,b) составляет новое множество, называемое прямым произведением А и В. Прямое произведение обозначается А×В.

4.1.2.Вещественные числа и их изображение на числовой оси Основные свойства рациональных чисел

Основным понятием математики являются числа натурального ряда:

def

N ≡ 1,2,3,..., n,... которые появились в результате счета предметов.

def

Целые числа: z ≡ −...−3,−2,−1,01, ,2,3,...

Рациональным числом называется число, представимое в виде отношения двух це-

В курсе элементарной математики вводились определения операций сложения и умножения рациональных чисел, давалось правило сравнения этих чисел, доказывались простейшие свойства.

Поэтому перечислим без доказательства основные свойства рациональных чисел, вытекающие из соответствующих свойств целых чисел.

Главную роль среди свойств играют три правила:

−правило сравнения;

−правило образования суммы;

−правило образования произведения.

1. Правило сравнения: любые два рациональные числа а и b связаны одним и только одним из трех знаков >, <, =, причем если а>b, то b< а.

Правило сравнения рациональных чисел формулируется так: два неотрицательных

p1q 2 и p 2q1 ; два неположительных рациональных числа а и b связаны тем же знаком, что

и два неотрицательных числа |b| и |а| ; если а – неотрицательное, а b – отрицательное число, то а>b.

Правило сравнения обладает следующим свойством:

70