
Высшая математика
.pdf
Международный консорциум «Электронный университет»
Московский государственный университет экономики, статистики и информатики
Евразийский открытый институт
А.Н. Малахов, Н.И. Максюков, В.А. Никишкин
Высшая математика
Учебно-методический комплекс
Москва 2008
УДК – 517 ББК – 22.11 В – 937
Малахов А.Н., Максюков Н.И., Никишкин В.А. ВЫСШАЯ МАТЕМАТИКА:
Учебно-методический комплекс. – М.: Изд. центр ЕАОИ. 2008. – 315 с.
В пособии представлены основные разделы математики, необходимые для успешного усвоения общетеоретических и специальных дисциплин в области экономики, менеджмента, статистики, бизнеса и информационных технологий.
Пособие предназначено для студентов и слушателей, обучающихся на всех формах обучения с использованием дистанционных образовательных технологий, а также для преподавателей высших и средних специальных учебных заведений.
Авторы: Малахов Александр Николаевич,
кандидат физико-математических наук, доцент
Максюков Николай Иванович,
доцент
Никишкин Валерий Александрович,
кандидат физико-математических наук, доцент
ISBN 978-5-374-00101-3 |
© Максюков Николай Иванович, 2008 |
|
© Малахов Александр Николаевич, 2008 |
|
© Никишкин Валерий Александрович, 2008 |
|
© Евразийский открытый институт, 2008 |
Издание 3-е Выпуск 5-й
2
|
|
ОГЛАВЛЕНИЕ |
|
УЧЕБНОЕ ПОСОБИЕ........................................................................................................ |
5 |
||
|
|
Введение.......................................................................................................................... |
6 |
1. |
|
Векторная алгебра.......................................................................................................... |
7 |
2. |
|
Кривые второго порядка................................................................................................ |
32 |
3. |
|
Аналитическая геометрия в пространстве................................................................... |
53 |
4. |
|
Введение в математический анализ.............................................................................. |
66 |
5. |
|
Дифференциальное исчисление.................................................................................... |
107 |
6. |
|
Неопределенный интеграл............................................................................................. |
148 |
7. |
|
Определенный интеграл и его геометрические приложения..................................... |
169 |
8. |
|
Обобщение понятия определенного интеграла. Несобственные интегралы............ |
191 |
9. |
|
Функции нескольких переменных................................................................................ |
198 |
10. |
Двойные интегралы........................................................................................................ |
236 |
|
11. |
Ряды ................................................................................................................................ |
246 |
|
12. |
Дифференциальные уравнения..................................................................................... |
265 |
|
Решение типовых задач контрольных работ................................................................. |
287 |
||
Задания для контрольных работ...................................................................................... |
314 |
||
Выводы.................................................................................................................................. |
327 |
||
Вопросы к экзамену ............................................................................................................ |
329 |
||
РУКОВОДСТВО ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ................................................. |
335 |
||
1. |
Цели, задачи изучения дисциплины и сферы профессионального применения......... |
336 |
|
2. |
Необходимый объем знаний для изучения дисциплины............................................... |
336 |
|
3. |
Перечень тем и подтем...................................................................................................... |
336 |
|
|
|
Тема 1. Векторная алгебра........................................................................................ |
336 |
|
|
Тема 2. Геометрия на плоскости и в пространстве................................................. |
337 |
3
Тема 3. Вещественные и комплексные числа. ........................................................ |
339 |
||
Тема 4. Числовые последовательности.................................................................... |
340 |
||
Тема 5. Понятия функции. Элементарные функции. Предел функции................ |
342 |
||
Тема 6. Непрерывность функций............................................................................. |
344 |
||
Тема 7. |
Производная и дифференциал функции. ................................................... |
345 |
|
Тема 8. |
Приложения производной. .......................................................................... |
347 |
|
Тема 9. |
Неопределенный интеграл. ......................................................................... |
348 |
|
Тема 10. |
Определенный интеграл. ........................................................................... |
350 |
|
Тема 11. |
Функции нескольких переменных............................................................ |
352 |
|
Тема 12. |
Ряды. ............................................................................................................ |
355 |
|
Тема 13. |
Обыкновенные дифференциальные уравнения....................................... |
357 |
|
4. Литература.......................................................................................................................... |
|
|
359 |
4
Учебное пособие
5
Введение
Знания, приобретаемые студентом в результате изучения математики, играют важнейшую роль в процессе его обучения в институте. Они необходимы для успешного усвоения общетеоретических и специальных дисциплин в области экономики, менеджмента, статистики, бизнеса и информационных технологий. Математические методы широко используются для решения самых разнообразных задач техники, экономики и финансов, планирования и прогнозирования, анализа финансовой и экономической деятельности. Поэтому студент не должен забывать, что и после окончания вуза он не раз столкнется с необходимостью применения математики в практической деятельности.
Учебные планы инженерно-экономических, экономических специальностей, специальностей в области статистики, менеджмента, бизнеса, информационных технологий и юриспруденции предусматривают изучение курса «Высшая математика».
Объем и содержание этого курса определяются программами, утвержденными Учебно-методическим управлением министерства общего и профессионального образования Российской Федерации и не зависит от формы обучения (дневное, вечернее, заочное, дистанционное).
Данное учебное пособие соответствует учебной программе по курсу высшей математики.
При написании данного пособия была использована следующая литература:
1.Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1987 г.
2.Ильин В.А., Позняк Э.Г. Основы математического анализа. Тт. 1–2. – М.: Наука,
1979 г.
3.Овчинников П.Ф. и др. Высшая математика К.: Высшая школа, 1989 г.
4.Коровин Ю.В., Никишкин В.А. Введение в математический анализ. – М.:
МЭСИ, 1983 г.
5.Коровин Ю.В., Никишкин В.А. Методические указания по изучению курса «Высшая математика».
6.Малахов А.Н. Высшая математика. – М.: МЭСИ, 1997 г.
6

1.ВЕКТОРНАЯ АЛГЕБРА
1.Векторная алгебра
1.1.Понятие вектора и линейные операции над векторами
1.1.1. Понятие вектора
Геометрическим вектором, или просто вектором, будем называть направленный отрезок.
Обозначать вектор будем либо как направленный отрезок символом AB , где точки
A и B обозначают соответственно начало и конец данного вектора, либо символом a .
B
a
A
Начало вектора называют точкой его приложения. Длину вектора будем обозначать
символом модуля: AB или a .
Вектор называется нулевым, если совпадают его начало и конец. Нулевой вектор имеет длину равную нулю.
Векторы называются коллинеарными, если они лежат на параллельных прямых.
a |
b |
a
b
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.
a
b
a b
Точка приложения вектора может быть выбрана произвольно, поэтому изучаемые векторы называют свободными.
1.1.2. Линейные операции над векторами
Линейными операциями называют операцию сложения векторов и операцию умножения векторов на вещественные числа.
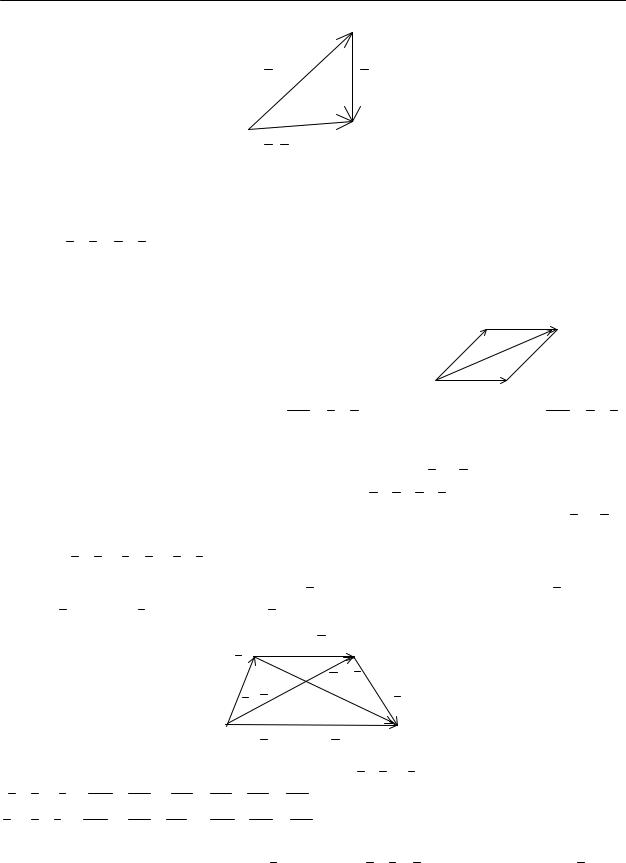
Определение 1. Суммой |
a |
+ |
b |
двух векторов |
a |
и |
b |
называется вектор, идущий |
||||||||
из начала вектора |
a |
в конец вектора |
b |
при условии, |
что вектор |
b |
приложен к концу |
|||||||||
вектора |
a |
. |
|
|
|
|
|
|||||||||
7
1. ВЕКТОРНАЯ АЛГЕБРА
a b
a+b
Это правило называют “правилом треугольника”.
Свойства сложения векторов:
1. a + b = b + a
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Приложим два произвольных вектора a |
и b |
|
|
|
|
|
||||||||||||||||
к общему началу 0. Обозначим A и B концы векторов |
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
B |
a |
|
C |
||||||||||||||||||||
и |
b |
|
соответственно и рассмотрим параллелограмм |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
b |
|
|
|
b |
|||||||||||||||||||||
OBCA. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
BC |
= |
OA |
= |
a |
, |
AC |
= |
OB |
= |
b |
. |
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
a |
A |
|
|
|
|||||||||||||||||
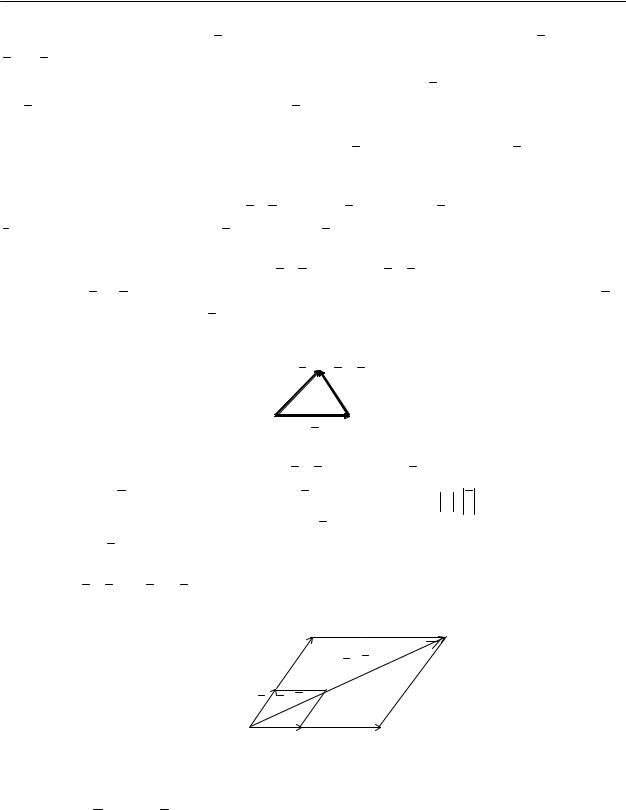
Из определения 1 и ∆OAC следует, что OC = a + b , а из ∆OBC следует, что OC = b + a , ч.т.д.
Замечание. При доказательстве свойства 1 нами получено правило сложения векторов, называемое “правилом параллелограмма”: если векторы a и b приложены к общему началу и на них построен параллелограмм, то сумма a + b ( b + a ) этих векторов представляет собой диагональ этого параллелограмма, идущую из общего начала векторов a и b .
2. (a + b)+ c = a + (b + c)
Доказательство. Приложим вектор a к произвольной точке 0, вектор b к концу
вектора a и вектор c к концу вектора b .
A |
b |
B |
a |
|
b + с |
|
|
|
a + b |
|
c |
0 |
|
C |
(a + b) + c = a + (b + c)
Обозначим буквами A, B, C концы векторов a , b и c , тогда
(a + b) + c = (OA + AB) + BC = OB + BC = OC
a+ (b + c) = OA + (AB + BC) = OA + AC = OC , ч.т.д.
3.Существует нулевой вектор 0 такой, что a + 0 = a для любого вектора a . Это свойство вытекает из определения 1.
8
1. ВЕКТОРНАЯ АЛГЕБРА
4. Для любого вектора a существует противоположный ему вектор - a такой, что a +(−a) = 0 .
Для доказательства этого свойства определим вектор - a , противоположный векто-
ру a , как вектор, коллинеарный вектору a , имеющий с ним одинаковую длину и противоположное направление.
Взятая по определению 1 сумма вектора a с таким вектором - a дает нулевой вектор.
Определение 2. Разностью a −b вектора a и вектора b называется такой вектор
c , который в сумме с вектором b дает вектор a .
Из определения 2 и из правила треугольника (определение 1) сложения векторов вытекает правило построения разности a −b : разность a −b приведенных к общему началу векторов a и b представляет собой вектор, идущий из конца вычитаемого вектора b в
конец уменьшаемого вектора a .
a a −b
0
b
Определение 3. Произведением α a (a α) вектора a на вещественное число α называется вектор b , коллинеарный вектору a , имеющий длину α a , и имеющий направ-
ление, совпадающее с направлением вектора a в случае α>0 и противоположное направ-
лению вектора a в случае α<0.
Свойства операции умножения вектора на число: 5. α(a + b) = αa +αb
αa
α(a + b)
a a + b
0
|
α |
b |
b |
При “растяжении” сторон параллелограмма в α раз в силу свойств подобия диагональ также “растягивается” в α раз, т.е.
αа +αb = α(а + b )
6.(α+β)а = αа +βа .
7.α(βа) = (αβ)а .
Последние два свойства очевидны из геометрических соображений.
9

1.ВЕКТОРНАЯ АЛГЕБРА
1.1.3.Понятие линейной зависимости векторов
Линейной комбинацией n векторов a1, a 2 , ..., a n будем называть сумму произведений этих векторов на произвольные вещественные числа:
α1a1 +α2 a 2 +...+αn a n ; |
(1) |
где α1,α2,... αn- любые вещественные числа.
Определение 1. Векторы a1, a 2 , ..., a n называются линейно зависимыми, если найдутся такие вещественные числа α1,α2,...,αn, из которых хотя бы одно отлично от нуля,
что линейная комбинация векторов a1, a 2 , ..., a n с указанными числами |
обращается в |
|
нуль: |
|
|
α1a1 +α2 a 2 +...+αn a n |
= 0 |
|
Векторы a1, a 2 , ..., a n |
не являющиеся линейно зависимыми будем |
называть ли- |
нейно независимыми. |
|
|
Приведем другое определение линейно независимых векторов.
Определение 2. Векторы a1 ,a2 ,...,an называются линейно независимыми, если равенство нулю их линейной комбинации (1) возможно лишь в случае, когда числа
α1=α2=,...,=αn=0
Из определений 1 и 2 следуют два утверждения:
1. Если хотя бы один из векторов a1, a 2 , ..., a n является нулевым, то эти векторы явля-
ются линейно зависимыми.
2. Если среди n векторов какие-либо (n-1) векторов линейно зависимы, то и все n векторов линейно зависимы.
1.1.4. Линейные комбинации двух векторов
Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Доказательство.
1). Необходимость. Пусть векторы a и b линейно зависимы. Докажем их коллинеарность.
По определению линейной зависимости найдутся такие вещественные числа α и β, хотя бы одно из которых не равно нулю, что справедливо равенство
αa +βb = 0
Пусть β≠0. Тогда b = − αβ a .
Обозначив λ = − αβ ; получим b = λa .
Необходимость доказана.
2). Достаточность. Пусть векторы a и b коллинеарны. Докажем, что они линейно зависимы. Если хотя бы один из них нулевой, то a и b линейно зависимы.
10
