Контрольная работа по эконометрике №2
Выполнил:
Студент группы ДЭМ-202
Лысенко Руслан
Вариант 4
1.Из предложенных данных вычеркните строчку с номером, соответствующим последней цифре номера зачетной книжки.
Данные 4-го варианта:
|
T |
Y |
X1 |
X2 |
X3 |
X4 |
|
1 |
30,8 |
459,7 |
39,5 |
55,3 |
79,2 |
|
2 |
31,2 |
492,9 |
37,3 |
54,7 |
77,4 |
|
3 |
35,6 |
560,3 |
39,3 |
69,8 |
80,4 |
|
4 |
38,4 |
717,8 |
40,1 |
70 |
93,7 |
|
5 |
40,4 |
768,2 |
38,6 |
73,2 |
106,1 |
|
6 |
40,3 |
843,3 |
39,8 |
67,8 |
104,8 |
|
7 |
41,8 |
911,6 |
39,7 |
79,1 |
114 |
|
8 |
40,4 |
931,1 |
52,1 |
95,4 |
124,1 |
|
9 |
40,7 |
1021,5 |
48,9 |
94,2 |
127,6 |
|
10 |
40,1 |
1165,9 |
58,3 |
123,5 |
142,9 |
|
11 |
42,7 |
1349,6 |
57,9 |
129,9 |
143,6 |
|
12 |
44,1 |
1449,4 |
56,5 |
117,6 |
139,2 |
|
13 |
50,6 |
1759,1 |
61,6 |
129,8 |
203,3 |
|
14 |
50,1 |
1994,2 |
58,9 |
128 |
219,6 |
|
15 |
51,7 |
2258,1 |
66,4 |
141 |
221,6 |
|
16 |
52,9 |
2478,7 |
70,4 |
168,2 |
232,6 |
2.Постройте уравнения регрессии со значимыми коэффициентами, используя пошаговый алгоритм регрессионного анализа. Требуется построить и сравнить ур-я регрессии вида:
1.
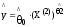-функция
спроса
2.
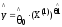-функция
потребления
3.
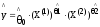-функция
спроса и потребления
4.
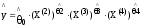-функция
спроса с учетом цены на товары заменители
Уравнения являются нелинейными, поэтому для построения регрессионных моделей необходимо привести их к линейному виду, а именно прологарифмировать.
|
ln Y |
ln X1 |
ln X2 |
ln X3 |
ln X4 |
|
3,42751469 |
6,130574103 |
3,676300672 |
4,012772909 |
4,371976299 |
|
3,440418095 |
6,200306314 |
3,618993327 |
4,001863709 |
4,348986781 |
|
3,572345638 |
6,328472355 |
3,671224519 |
4,24563401 |
4,387014176 |
|
3,64805746 |
6,576190979 |
3,691376334 |
4,248495242 |
4,540098189 |
|
3,698829785 |
6,644050116 |
3,653252276 |
4,293195421 |
4,664382046 |
|
3,696351469 |
6,737322767 |
3,683866912 |
4,216562195 |
4,652053772 |
|
3,73289634 |
6,815201297 |
3,681351188 |
4,370712875 |
4,736198448 |
|
3,698829785 |
6,836366683 |
3,953164949 |
4,558078578 |
4,821087692 |
|
3,706228092 |
6,929027414 |
3,889777396 |
4,545420182 |
4,848900371 |
|
3,691376334 |
7,0612486 |
4,065602093 |
4,816241156 |
4,962145085 |
|
3,75419892 |
7,207563531 |
4,058717385 |
4,866764924 |
4,967031657 |
|
3,786459782 |
7,278904957 |
4,034240638 |
4,767289035 |
4,935911748 |
|
3,923951576 |
7,472557594 |
4,120661871 |
4,865994804 |
5,314682721 |
|
3,914021008 |
7,597998246 |
4,075841091 |
4,852030264 |
5,39180771 |
|
3,945457782 |
7,722279031 |
4,195697056 |
4,94875989 |
5,400873955 |
|
3,968403339 |
7,815489508 |
4,254193263 |
5,125153748 |
5,44932024 |
1 Модель:
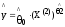-функция
спроса; отражает прямую зависимость
потребления цыплят от стоимости 1-го
фунта цыплят.
Проводим регрессионный анализ с помощью функции в EXCEL.
Для
построения модели необходимо вычислить
коэффициент b0,
который рассчитываетя с помощью функции
в EXCEL
exp.
Вычисляем экспоненциальную функцию
для значения Y-пересечения.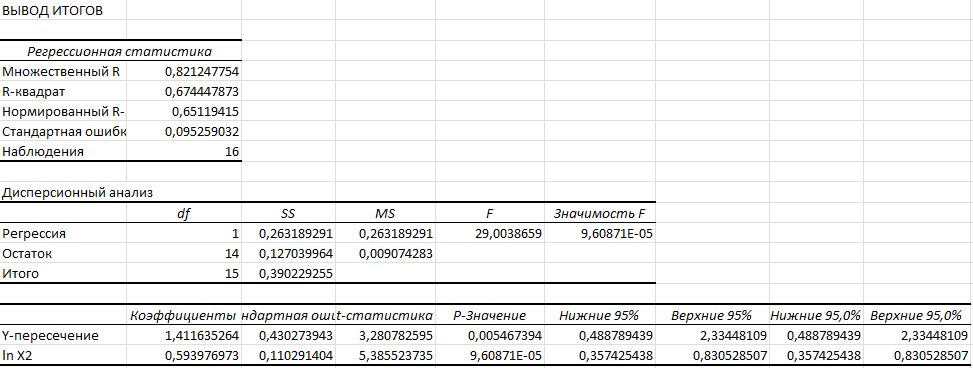
|
b0 |
4,102658854 |
Коэффициент b2 в данном случае равен 0,59.
Теперь получены все необходимые данные для построения регрессионной модели. Получается следующее уравнение:
|
Функция спроса |
|
Y=4,102*X2^0,59 |
Так как эта функция отражает прямую зависимость потребления цыплят от стоимости 1-го фунта цыплят, а коэффициент эластичности (b2)>0, то модель является неинтерпретируемой: ведь потребление цыплят по логике не должно увеличиваться с увеличением цены на них, что также говорит о том, что, видимо, мы не обладаем достаточными данными, например, об уровне инфляции или доходе населения.
Далее
рассчитываем
среднюю
относительную ошибку аппроксимации
.
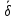Для этого делим остатки, полученные в
ходе регрессионного анализа с помощьюEXCEL,
на значения lnY,
а затем поделить сумму вычисленных
значений на количество наблюдений (в
нашем случае оно равно 16) и умножить на
100%. Ниже приведены результаты вычисления:
|
|
0,048944653 |
|
|
0,035116625 |
|
|
0,005574055 |
|
|
0,012014519 |
|
|
0,031698348 |
|
|
0,026129574 |
|
|
0,036064018 |
|
|
0,016463161 |
|
|
0,004275337 |
|
|
0,036607742 |
|
|
0,018171922 |
|
|
0,005657402 |
|
|
0,016498177 |
|
|
0,020804689 |
|
|
0,0105628 |
|
|
0,007528277 |
|
Сумма |
0,332111298 |
|
Дельта (%) |
2,075695613 |
Значение данного показателя в 2% говорит об адекватности модели (<10%). Фактическое значение результативного признака y отличается от теоретических значений, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, и лучше качество модели.
Далее необходимо проверить модель на наличие автокорреляции остатков по критерию Дарбина-Уотсона. Наличие автокорреляции означает, что модель выбрана неудачно, так как последовательные значения остатков не обладают свойствами независимости и могут коррелировать между собой. Фактическое значение вычисляется по формуле:
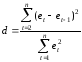
Фактическое значение необходимо сравнить с табличными, критическими.
Результаты для данной модели:
|
ei |
ei^2 |
ei-ei-1 |
(ei-ei-1)^2 |
|
-0,167758519 |
0,028142921 |
0 |
0 |
|
-0,12081587 |
0,014596475 |
0,046942648 |
0,002203612 |
|
-0,019912453 |
0,000396506 |
0,100903418 |
0,0101815 |
|
0,043829655 |
0,001921039 |
0,063742107 |
0,004063056 |
|
0,117246792 |
0,01374681 |
0,073417138 |
0,005390076 |
|
0,096584088 |
0,009328486 |
-0,020662705 |
0,000426947 |
|
0,134623241 |
0,018123417 |
0,038039153 |
0,001446977 |
|
-0,060894429 |
0,003708131 |
-0,19551767 |
0,038227159 |
|
-0,015845375 |
0,000251076 |
0,045049054 |
0,002029417 |
|
-0,135132954 |
0,018260915 |
-0,119287579 |
0,014229527 |
|
-0,06822101 |
0,004654106 |
0,066911944 |
0,004477208 |
|
-0,021421524 |
0,000458882 |
0,046799486 |
0,002190192 |
|
0,064738048 |
0,004191015 |
0,086159572 |
0,007423472 |
|
0,081429991 |
0,006630843 |
0,016691943 |
0,000278621 |
|
0,041675081 |
0,001736812 |
-0,03975491 |
0,001580453 |
|
0,029875238 |
0,00089253 |
-0,011799842 |
0,000139236 |
|
|
0,127039964 |
|
0,094287454 |
|
DW |
0,742187348 |
|
|
|
|
d1 |
1,1 |
|
d2 |
1,37 |
DW<d1, это говорит о том, что существует положительная автокорреляция, модель неадекватна.