Глава 4. Кластерный и дискриминантный анализ

4.1. Классификация семей по анализируемой структуре расходов

По данным, представленным в табл. 4.1, провести классификацию n=5 семей по двум показателям: уровень расходов (млн.руб.) за летние месяцы на культурные нужды, спорт и отдых -х⁽¹⁾и питаниех⁽²⁾:

Таблица 4.1.

№ семьи (i)	1	2	3	4	5
хi(1)	2	4	8	12	13
xi(2)	10	7	6	11	9

Классификацию провести по иерархическому агломеративному алгоритму с использованием обычного и взвешенного (w₁=0,05;w₂=0,95) евклидова расстояния, а также принципов: “ближайшего” и “дальнего” соседа, центра тяжести и средней связи.

Сравнить полученные результаты и обосновать выбор окончательного варианта классификации.

Примечание:На основании предварительного качественного анализа было выдвинуто предположение, что по потребительскому поведению три первые семьи принадлежат одной типологической группе, а две последние (4 и 5) - другой, что согласуется с расположением пяти наблюдений на плоскости, представленных на рис.4.1.

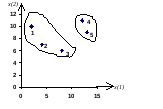
Рис.4.1. Исходные данные для классификации

Решение. 1. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип “ближайшего соседа”.

Согласно обычной евклидовой метрике расстояние между наблюдениями 1 и 2 равно

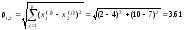, (4.1)

очевидно, что _1,1=0.

Аналогично находим расстояния между всеми пятью наблюдениями и строим матрицу расстояний

.

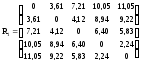Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки _4,5=2,24 и поэтому объединим их в один кластер. После объединения объектов имеем четыре кластера: S₁, S₂, S₃, S_(4,5).

Расстояние между кластерами будем находить по принципу “ближайшего соседа”, воспользовавшись формулой пересчета. Так расстояние между кластером S₁и кластером S_(4,5)равно:

(4.2)

Мы видим, что расстояние _1,(4,5)равно расстоянию от объекта 1 до ближайшего к нему объекта, входящего в кластер S_(4,5), т.е._1,(4,5)=_1,4=10,05. Проводя аналогичные расчеты, получим матрицу расстояний

.

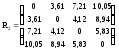Объединим наблюдения 1 и 2, имеющие наименьшее расстояние _1,2=3,61. После объединения имеем три кластера S_(1,2), S₃и S_(4,5).

Вновь строим матрицу расстояний. Для этого необходимо рассчитать расстояние до кластера S_(1,2). Воспользуемся матрицей расстояний R₂.

Например, расстояние между кластерами S_(4,5)и S_(1,2)равно:

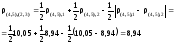
Как видим, оно равно расстоянию от кластера S_(4,5)до ближайшего объекта, входящего в кластер S_(1,2), то есть_(4,5),(1,2)=_(4,5),2=8,94.

Проведя аналогичные расчеты, получим матрицу расстояний

.

Объединим кластеры S_(1,2)и S₍₃₎, расстояние между которыми, согласно матрице R₃, минимально_(1,2),3=4,12. В результате этого получим два кластера: S_(1,2,3)и S_(4,5). Матрица расстояний будет иметь вид:

.

Из матрицы R₄следует, что на расстоянии_{(1,2,3),(4,5)}=5,83 все пять наблюдений объединяются в один кластер. Результаты кластерного анализа представим графически в виде дендрограммы (рис.4.2).

Рис. 4.2. Дендрограмма (обычное евклидово расстояние, ближайший сосед)

На основании графического представления результатов кластерного анализа (рис.4.2) можно сделать вывод, что наилучшим является разбиение пяти регионов на два кластера: S_(1,2,3)и S_(4,5), когда пороговое расстояние находится в интервале 4,12<_пор<5,83.

Напомним, что выводы нами сделаны для случая, когда для измерения расстояния выбрано “обычное евклидово расстояние” и принцип “ближайшего соседа”.

2. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип “дальнего соседа”.

Как и в случае (1), мы используем обычное евклидово расстояние, поэтому матрица R₁остается без изменения. Согласно агломеративному алгоритму объединяются в один кластер объекты 4 и 5, как наиболее близкие_4,5=2,24. После объединения имеем четыре кластера: S₁, S₂, S₃и S_(4,5).

В виду того, что расстояние между кластерами измеряем по принципу “дальнего соседа”, то воспользуемся формулой пересчета, приняв =1/2, а не ‑1/2, как в случае (1). Тогда, например, расстояние между кластером S₁и кластером S_(4,5)определяется по формуле:

,

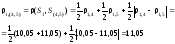Таким образом, расстояние _1,(4,5)равно расстоянию от объекта 1 до наиболее отдаленного от него объекта, входящего в кластер S_(4,5), то есть_1,(4,5)=_1,5=11,05.

Аналогично рассматриваются все остальные элементы матрицы расстояния

.

Объединим объекты 1 и 2 в один кластер, как наиболее близкие (согласно матрице R₂),_1,2=3,61.

После объединения имеем три кластера: S_(1,2), S₃и S_(4,5).

Строим матрицу расстояний R₃, воспользовавшись принципом “дальнего соседа”.

.

Объединим кластеры S₃ и S_(4,5), расстояние между которыми_3,(4,5)=6,40 минимально, и получим два кластера: S_(1,2)и S_(3,4,5), расстояние между которыми определяется по матрицеи равно_{(1,2),(3,4,5)}=11,05.

Графические результаты классификации представлены на рис.4.3.

Рис.4.3 Дендрограмма (обычное евклидово расстояние, дальний сосед)

Как и в предыдущем случае наилучшим является разбиение регионов на два кластера (рис. 4.3): S_(1,2) и S_(3,4,5), после предпоследнего шага классификации, когда интервал измерения расстояния объединения наибольший 6,40_пор11,05.

Таким образом, используя принцип “дальнего соседа” мы получили разбиение регионов на два кластера S_(1,2) и S_(3,4,5), которое отличается от разбиения по принципу “ближайшего соседа”: S_(1,2,3) и S_(4,5).

3. Классификация на основе обычного евклидова расстояния и принципа “ центра тяжести”.

Так как мы используем обычное евклидово расстояние, то матрица R₁остается без изменения. Согласно агломеративному алгоритму объединяются в кластер S_(4,5)объекты 4 и 5, как наиболее близкие_4,5=2,24.

Кластер S_(4,5)характеризуется в дальнейшем его центром тяжести, определяемым вектором средних.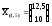

Расстояние от этого кластера до первого наблюдения равно:

.

Тогда матрица расстояний примет вид:

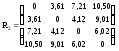
Объединим объекты 1 и 2, расстояние между которыми _1,2=3,61 минимальное. Кластер характеризуется центром тяжести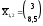, расстояния от которого до кластера S_(4,5)равно:

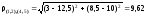
Тогда матрица расстояний примет вид:

.

В матрице R₃минимальное расстояние_(1,2),3=5,59, поэтому образуем кластер S_(1,2,3)и определим его вектор средних.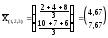

Найдем расстояние между S_(1,2,3)и S_(4,5)

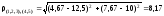
на котором все пять объектов объединяются в один кластер. Графически результаты классификации представлены на рис. 4.4

Рис.4.4 Дендрограмма (обычное евклидово расстояние, принцип “центра тяжести”)

Из рис. 4.4 видно, что наибольший скачок в расстояниях объединения  имеет место на последнем шаге, поэтому целесообразно выбрать разбиение на два кластера S_(1,2,3)и S_(4,5), что совпадает со случаем (1).

4.Классификация на основе обычного евклидова расстояния и принципа “средней связи”.

Используя матрицу R₁, согласно агломеративному алгоритму объединим кластеры S₄и S₅в один S_(4,5), так как расстояние между ними_4,5=2,24^‑минимально.

Расстояние от кластера S_(4,5)до остальных кластеров определим по принципу “средней связи” на основе матрицыR₁. Например:

.

Тогда матрица расстояний имеет вид:

.

Объединим, как наиболее близкие _1,2=3,61, кластеры S₁и S₂. Тогда расстояния от S_(1,2)до остальных кластеров S_(4,5) равна:

,

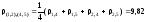а матрица расстояний имеет вид:

Объединим, как наиболее близкие _(1,2),3=5,41, кластеры S_(1,2)и S₃ и определим расстояния от S_(1,2,3)до S_(4,5)

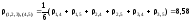
на котором все пять объектов объединились в один кластер. Графически результаты классификации представлены на рис. 4.5

Рис.4.5 Дендрограмма (обычное евклидово расстояние, принцип средней связи)

Из рис. 4.5 следует, что целесообразным является разбиение на два кластера S_(1,2,3)и S_(4,5).

Таким образом, сравнивая результаты 4-х разбиений пяти регионов на однородные группы, можно отметить, что наиболее устойчивым, а отсюда и предпочтительным, является разбиение на два кластера S_(1,2,3)и S_(4,5), что согласуется с рис. 4.1. Только в одном случае из четырех, при использовании принципа “дальнего соседа” получено разбиение S_(1,2)и S_(3,4,5).

Во всех предыдущих алгоритмах классификации мы предполагали, что оба показателя х⁽¹⁾их⁽²⁾одинаково значимы (использовалось обычное евклидово расстояние). Теперь откажемся от этого предположения.

5. Классификация на основе “взвешенного евклидова расстояния” и принципа “ближайшего соседа”.

Предположим, что показатель х⁽¹⁾менее важен для классификации, чемх⁽²⁾. В этой связи припишем им “веса”₁=0,05 и₂=0,9. Напомним, что взвешенное евклидово расстояние междуi-м иl-м наблюдениями определяется по формуле:

. (4.3)

Тогда расстояние между объектами 1 и 2 равно:

.

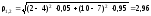Аналогично находим все остальные расстояния и строим матрицу расстояний:

.

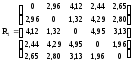Объединив S₂и S₃, имеющих минимальное расстояние_2,3=1,32 в кластер S_2,3, и применив принцип “ближайшего соседа”, получим матрицу расстояний:

.

Образовав на расстоянии _4,5=1,96 кластер S_4,5вновь построим матрицу расстояний:

Объединим S₁и S_4,5, имеющих минимальное расстояние_(4,5)1=2,43,в кластер S_(1,4,5)и получим матрицу расстояний

.

Следовательно, на расстоянии _{(1,4,5),(2,3)}=2,80 объединяются кластеры S_(1,4,5)и S_(2,3)и все пять объектов образуют один кластер.

Результаты классификации представлены графически на рис.4.6

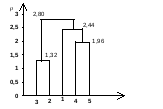
Рис.4.6 Дендрограмма (взвешенное евклидово расстояние, принцип ближайшего соседа)

Как и прежде, отдадим предпочтение разбиению на два кластера; мы получаем третий вариант разбиения, а именно S_(2,3)и S_(1,4,5).

Таким образом, используя пять алгоритмов кластерного анализа, мы получили три варианта разбиения пяти семей на две статистически однородные группы. С одной стороны это свидетельствует о гибкости (возможностях) методов кластерного анализа, а с другой- о необходимости использования экономических (содержательных) и статистических критериев для выбора наилучшего варианта классификации. При этом часто бывает полезной априорная информация об исследуемом явлении. В нашем примере, окончательно следует остановиться на разбиении S_(1,2,3)и S_(4,5), как наиболее устойчивом. Это разбиение получено по трем алгоритмам из пяти. Кроме того, оно согласуется с данными априорного, качественного анализа.