2.4. Системы поддержки принятия решений

Системы поддержки принятия решений существуют очень давно: это военные советы, коллегии министров, всевозможные совещания, аналитические центры и т.д. Хотя они никогда не назывались системами поддержки принятия решений, но выполняли именно их задачи.

Увеличение объема информации, поступающей в органы управления и непосредственно к руководителям, усложнение решаемых задач, необходимость учета большого числа взаимосвязанных факторов и быстро меняющаяся обстановка настоятельно требуют использовать вычислительную технику в процессе принятия решений. В связи с этим появился новый класс вычислительных систем – системы поддержки принятия решений.

Термин «система поддержки принятия решений» появился в начале семидесятых годов, и за это время было дано большое число определений этого понятия:

1. Системы поддержки принятия решений являются человеко-машинными объектами, которые позволяют лицам, принимающим решения, использовать данные, знания, объективные и субъективные модели для анализа и решения слабоструктурированных и неструктурированных проблем.

2. Система поддержки принятия решений – это компьютерная система, позволяющая ЛПР сочетать собственные субъективные предпочтения с компьютерным анализом ситуации при выборе рекомендаций в процессе принятия решения.

3. Система поддержки принятия решений – компьютерная информационная система, используемая для различных видов деятельности при принятии решений в ситуациях, где невозможно или нежелательно иметь автоматическую систему, полностью выполняющую весь процесс.

Все три определения не противоречат, а дополняют друг друга и достаточно полно характеризуют систему поддержки принятия решений.

Человеко-машинная процедура принятия решений с помощью систем поддержки представляет собой циклический процесс взаимодействия человека и компьютера. Цикл состоит из фазы анализа и постановки задачи для компьютера, выполняемой ЛПР, и фазы оптимизации (поиска решения), реализуемой компьютером.

Системы поддержки принятия решений:

• помогают произвести оценку обстановки, осуществить выбор критериев и оценить их относительную важность;

• генерируют возможные решения;

• осуществляют оценку решений и выбирают лучшее;

• обеспечивают постоянный обмен информацией об обстановке принимаемых решений и помогают согласовать групповых решения;

• моделируют принимаемые решения;

• осуществляют динамический компьютерный анализ возможных последствий принимаемых решений;

• производят сбор данных о результатах реализации принятых решений и осуществляют оценку результатов.

3. Оптимизационные модели

3.1 Оптимизационная модель затрат на рекламу .

Целью работы коммерческой фирмы является получение прибыли. Любое управленческое решение (будь то решение о количестве приобретаемого товара, или решение о назначении цены на реализуемый товар, или решение о подаче рекламы в газету и т.д.) будет влиять на прибыль в большую или меньшую сторону. В данной главе представлена методика, позволяющую определить, как и сколько тратить на рекламу.

Потери коммерческих фирм, связанные с неоптимальным проведением рекламной кампании, пожалуй, больше, чем остальные потери, связанные с неоптимальным управлением коммерческой фирмой. Особенно это касается фирм, только начинающих коммерческую деятельность и не ориентирующихся на рекламном рынке. Данная методика одинаково пригодна как для больших, так и для малых фирм (в том числе для предпринимателей). В то же время это требует определенных расходов по отслеживанию эффективности рекламы в различных СМИ (средствах массовой информации).

Пример оптимизации рекламной кампании

Допустим, фирма занимается мелкооптовой реализацией строительных товаров. Оборотного капитала хватает для оптимальной закупочной политики, на товар установлены оптимальные для данных условий цены [1], и имеются средства для дополнительных вложений в этот бизнес (например, прибыль, кредиты или другие источники средств). Рассмотрим возможности подачи рекламы в две строительные газеты - "Строительство" и "Строительные цены" (названия газет вымышлены). Предположим, что из маркетинговых исследований, проводимых в фирме, известно, сколько в среднем приходит клиентов по рекламе в одном выпуске этих газет. Сведем в таблицу 1 данные по количеству клиентов, пришедших по рекламе, в зависимости от размера рекламного модуля.

Табл. 1

Издание	Площадь рекламного модуля, кв. см.
	460	225	150	110	75	55	36	25
	Количество клиентов по рекламе на обложке
Строительство	-	24	-	23	-	19	-	-
Строительные цены	-	-	20	-	18	-	-	-
	Количество клиентов по рекламе внутри газеты
Строительство	8	8	-	8	-	6	-	4
Строительные цены	7	7	7	6	6	5	4	-

Предположим, что каждый клиент, пришедший по рекламе, приобретет товаров (работ, услуг) в среднем на сумму 1000 рублей. Допустим, что это принесет фирме 200 рублей чистой прибыли (без учета затрат на рекламу). Тогда для определения чистой прибыли за 1 месяц для различных объемов рекламы следует умножить данные табл. 1 на 200 рублей (табл. 2).

Табл. 2

Издание	Площадь рекламного модуля, кв. см.
	460	225	150	110	75	55	36	25
	Прибыль по рекламе на обложке, руб.
Строительство	-	4 800	-	4 600	-	3 800	-	-
Строительные цены	-	-	4 000	-	3 600	-	-	-
	Прибыль по рекламе внутри газеты, руб.
Строительство	1 600	1 600	-	1 600	-	1 200	-	800
Строительные цены	1 400	1 400	1 400	1 200	1 200	1 000	800	-

Теперь приведем расценки на рекламу в этих газетах (табл. 3).

Табл. 3

Издание	Площадь рекламного модуля, кв. см.
	460	225	150	110	75	55	36	25
	Расценки на рекламу на обложке, руб.
Строительство	-	5 400	-	2 900	-	1 700	-	-
Строительные цены	-	-	5 300	-	2 700	-	-	-
	Расценки на рекламу внутри газеты, руб.
Строительство	2 700	1 400	-	720	-	420	-	270
Строительные цены	3 900	1 900	1 300	900	600	460	300	-

И теперь для определения чистой прибыли с учетом затрат на рекламу остается из данных предпоследней таблицы вычесть данные последней:

Табл. 4

Издание	Площадь рекламного модуля, кв. см.
	460	225	150	110	75	55	36	25
Прибыль по рекламе на обложке с учетом затрат на рекламу, руб.
Строительство	-	-600	-	1 700	-	2 100	-	-
Строительные цены	-	-	-1 300	-	900	-	-	-
Прибыль по рекламе внутри газеты с учетом затрат на рекламу, руб.
Строительство	-1 100	200	-	880	-	780	-	530
Строительные цены	-2 500	-500	100	300	600	540	500	-

Естественно ожидать, что чем больше вложенный капитал, тем больше прибыль. Из последних двух таблиц видно, что до определенной степени это верно, но для больших по площади модулей становится неверным.

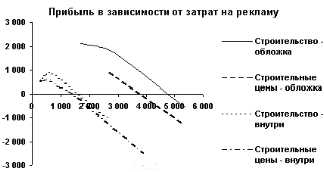
Из приведенных графиков видно, что вложения в рекламу в газете "Строительство" будут оптимальными. Чем большими средствами располагает фирма, тем большую площадь выгоднее взять, однако площадь 225 см² уже брать невыгодно, вместо этого лучше взять модуль 55 см² на обложке.

Однако здесь не была учтена возможность подачи рекламы в оба издания. Рассчитаем величину прибыли при условии подачи минимальных модулей в обе газеты. Из табл. 1 видно, что при этих условиях в фирму придут 4+4=8 клиентов, которые принесут 800+800=1600 руб. прибыли без учета затрат на рекламу и 530+500=1030 руб. прибыли с учетом затрат на рекламу. Затраты на рекламу в этом случае составят 270+300=570 руб. Однако последний результат справедлив только в том случае, если аудитории читателей обеих газет не пересекаются. То есть все читатели газеты "Строительство" не являются читателями газеты "Строительные цены". На самом же деле это не так, поскольку часть читателей газеты "Строительство" будут являться и читателями газеты "Строительные цены".

Допустим, что из 4-х клиентов, которые придут по рекламе в газете "Строительство" один будет также читателем газеты "Строительные цены" и был бы клиентом по рекламе в газете "Строительные цены". Таким образом, при подаче минимальных рекламных модулей в обе газеты клиентами станут уже не 8, а 7 человек. Что соответственно принесет 1 400 руб. прибыли без учета затрат на рекламу и 830 руб. прибыли с учетом затрат на рекламу. В наихудшем случае полного пересечения аудиторий обеих газет те 4 клиента, которые придут по рекламе в газете "Строительство" будут теми же 4-мя клиентами, которые придут по рекламе в газете "Строительные цены". В этом случае подача рекламы в обе газеты принесет всего 800 руб. прибыли без учета затрат на рекламу и 230 руб. прибыли с учетом затрат на рекламу.

Сведем в таблицу 5 величины прибыли при различных вариантах подачи рекламных модулей в обе газеты при условии 25% пересечения аудиторий:

Табл. 5.

Площадь рекламного модуля, кв. см.
110(с)+110(ц)	110(с)+75(ц)	55(с)+75(ц)	55(с)+55(ц)	55(с)+36(ц)	25(с)+36(ц)
Прибыль по рекламе на обложке с учетом затрат на рекламу, руб.
-	1 700	2 100	-	-	-
Прибыль по рекламе внутри газеты с учетом затрат на рекламу, руб.
880	1 180	1 080	1 070	1 080	830

В этой таблице буквой "с" обозначена газета "Строительство", а буквой "ц" - "Строительные цены".

Величины затрат на рекламу в этих случаях приводить не будем, их легко определить из таблицы 3. С учетом возможности подачи рекламы в оба издания построим график зависимости прибыли от затрат на рекламу.

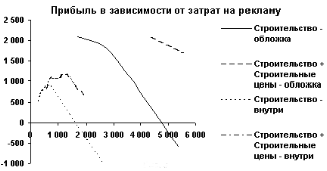
Из этого графика уже прорисовывается план оптимальной рекламной кампании. Сведем в таблицу величины максимальной прибыли в зависимости от величины рекламных затрат, которые может себе позволить фирма:

Табл. 6

Размеры модулей, см2		Сумма затрат		Прибыль
Строительство	Строительные цены	руб.	руб.
25	-	270	530
55	-	420	780
25	36	570	830
55	36	720	1 080
55 - обложка	-	1 680	2 120
55 - обложка	75 - обложка	4 400	2 100

И, соответственно, график зависимости максимальной прибыли от величины затрат на рекламу:

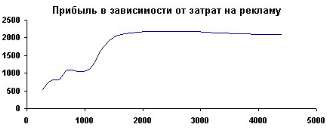
При условии еженедельности обеих рекламных газет, видим, что при еженедельном рекламном бюджете до 1 500 руб. оптимальная рекламная кампания будет включать в себя рекламу в этих двух газетах (при условии, что в остальных СМИ отдача по рекламе меньше). При возможности рекламных затрат больше этой суммы имеет смысл привлекать другие СМИ.

Приведем без доказательства следующее положение. Распределение затрат на рекламу будет оптимальным (т.е. приносить максимальную для данной величины рекламного бюджета прибыль), если рекламный бюджет будет распределяться между СМИ пропорционально рентабельности вложений в эту рекламу. Допустим, что фирма давала в течение полугода минимальный модуль в 5 печатных изданий, стоимость которых была одинакова. 1-е издание обеспечило увеличение прибыли (с учетом затрат на рекламу) на 100 тыс. руб., 2-е - на 60 тыс. руб., 3-е - на 40 тыс. руб., по 4-му и 5-му изданиям отдачи по рекламе не было. Предположим, что рекламный бюджет на следующий период составляет 40 тыс. руб. Для оптимального распределения рекламный бюджет должен быть распределен следующим образом. По 1-му изданию необходимо затратить 20 тыс. руб., по 2-му - 12 тыс. руб., по 3-му - 8 тыс. руб.

Рассматриваемая задача оптимизации рекламной кампании может быть сформулирована как целочисленная задача линейного программирования.

Введём двоичные переменные x_ij :

x_1j =1, если рекламный модуль площади j размещается на обложке газеты «Строительство», и x_1j =0 в противном случае;

x_2j =1, если рекламный модуль площади j размещается на обложке газеты «Строительные цены» и x_2j =0 в противном случае;

x_3j =1, если рекламный модуль площади j размещается внутри газеты «Строительство», и x_1j =0 в противном случае;

x_4j =1, если рекламный модуль площади j размещается внутри газеты «Строительные цены» и x_4j =0 в противном случае.

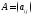
По условию задачи, x₁₁ =0, так как модуля площадью 460 нет на обложке газеты «Строительство». Чтобы запретить значение x₁₁ =1, вставим в матрицу расценок на рекламу 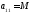, где М – очень большое число, примем, например М=99999. Аналогично поступим в остальных случаях, когда в таблице 3 стоят прочерки. Тогда матрица расценок на рекламу примет вид:

.

Аналогично поступим с матрицей 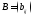чистой прибыли для различных объёмов рекламы, представленной в таблице 2, только теперь на места прочерков поставим. МатрицаВ имеет вид:

Матрица чистой прибыли с учётом затрат на рекламу С равна разности матриц В и А : .

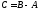Целевая функция f(X) равна сумме произведений

,

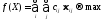ограничение на затраты имеет вид

,

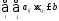где b – объём рекламного бюджета.

Поскольку предполагается, что внутри газеты и на обложке может быть не более одного модуля, то вводим ограничения на количество рекламных модулей

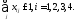
Напомним, что x_ij – двоичные переменные .

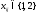Если учитывать пересечение круга читателей газет, то полученная целочисленная задача линейного программирования легко преобразуется для решения задачи оптимизации рекламной кампании в этом случае.