6.3. Сведения матричной игры к задаче линейного программирования [2, 3]

Если седловая точка отсутствует, то общим методом решения игры любой (конечной) размерности является сведение игры двух лиц с нулевой суммой к задаче линейного программирования. Из основного положения теории стратегических игр следует, что при использовании смешанных стратегий существует по меньшей мере одно оптимальное решение с ценой игры v, причем, 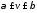, т.е. цена игры находится между ниж­ним и верхним значениями игры. Величина v неизвестна, но мож­но предположить, что v > 0. Это условие выполняется, поскольку путем преобразования матрицы всегда можно сделать все ее эле­менты положительными. Таким образом, если в исходной платеж­ной матрице имеется хотя бы один неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование в матрицу, все элементы которой строго положительны. Для этого достаточно увеличить все элементы исходной матрицы на одно и то же число 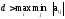, где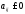. При таком преобразовании мат­рицы оптимальные стратегии игроков не изменяются.

Допустим, что смешанная стратегия игрока 1 складывается из стратегий A₁,A₂,…,A_m с вероятностями соответственно х₁, х₂,…,х_m (). Оптимальная смешанная стратегия игрока 2 скла­дывается из стратегий B₁, B₂,…,B_n с вероятностями y₁,y₂,…,y_n

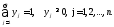
Условия игры определяются платежной матрицей

.

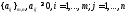Если игрок 1 применяет оптимальную смешанную стратегию, а игрок 2 — чистую стратегию B_j, то средний выигрыш игрока 1 (математическое ожидание выигрыша) составит х₁a_1j + х₂a_2j+…+x_ma_mj , j=1,…,n.

Игрок 1 стремится к тому, чтобы при любой стратегии игрока 2 его выигрыш был не менее чем цена игры v (смотри (3.1)) и сама цена игры была максимальной. Такое поведение игрока 1 описывается следующей моделью линейного программирования:

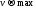(игрок 1 стремится максимизировать свой выигрыш),

х₁a₁₁ + х₂a₂₁+…+x_ma_ь1v

х₁a₁₂ + х₂a₂₂+…+x_ma_m2v

х₁a_1n + х₂a_2n+…+x_ma_mnv,

Преобразуем систему ограничений, разделив все члены неравенств на v (v >0) и обозначим t_i =x_i . Из условия х₁ + х₂+…+x_m =1 следует, что t₁ + t₂+…+t_m =1/v . В результате получаем следующую задачу линейного программирования:

t₁ + t₂+…+t_m min

t₁a₁₁ + t₂a₂₁+…+t_ma_ь11

t₁a₁₂ + t₂a₂₂+…+t_ma_m21 (3.3)

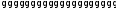
t₁a_1n + t₂a_2n+…+t_ma_mn1

t_i 0, i=1,…,m.

Поведению игрока 2 соответствует двойственная задача:

u₁ + u₂+…+u_n 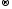max (эквивалентно v min: игрок 2 стремится минимизироиать свой средний проигрыш)

a₁₁u₁+a₁₂u₂+…+a_1nu_n1

a₂₁u₁+a₂₂u₂+…+a_2nu_n1 (3.4)

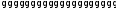
a_m1u₁+a_m2u₂+…+a_mnu_n1,

где u_j 0, j=1,…,n

Таким образом, для решения игры имеем пару симметричных двойст­венных задач линейного программирования. Используя свойство симметричности, можно решить одну из них, а решение второй задачи найти на основании оптимального плана двойствен­ной к ней задачи.

Задача (3.3) всегда имеет решение. Получив ее оптимальное решение t₁^*, t₂^*,…, t_m^*, можно найти цену игры v*=1/( t₁^*+ t₂^*+…+ t_m ), оптимальные значения x₁^*, x₂^*,…, x_m (x_i^*= t_i^*v*) и, следовательно, оптималь­ную стратегию игрока 1. Оптималь­ную стратегию игрока 2 находим по формуле y_i^*= u_i^*v* .

Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры v* нужно умень­шить на d.