
- •Содержание
- •1. Основные понятия и определения
- •1.1. Принятие решений как особый вид человеческой деятельности
- •1.2. Люди принимающие решения и их роль в процессе принятия решений
- •1.3. Альтернативы
- •1.4. Критерии
- •1.5. Оценка важности критериев
- •1.6. Многодисциплинарный характер науки о принятии решений
- •2. Анализ задач и методов принятия решений
- •2.1. Схема процесса принятия решений
- •Принятие решения Отыскание рациональных альтернатив
- •Разработка плана и реализация принятого решения Оценка фактически достигнутых результатов
- •2.2. Классификация задач принятия решений
- •2.3. Классификация методов принятия решений
- •2.4. Системы поддержки принятия решений
- •3. Оптимизационные модели
- •3.1 Оптимизационная модель затрат на рекламу .
- •3.2. Выбор оптимального медиа-плана кампании
- •Решение.
- •3.3. Оптимизационные модели составления медиа-плана в случае нескольких критериев (целевое программирование).
- •3.4. Построение кривой достижимости охвата по различным категориям телеаудитории (Парето-оптимальный подход).
- •4. Динамическое программирование
- •4.1. Основная идея и особенности вычислительного метода динамического программирования
- •4.2. Задачи управления запасами
- •4.2.1. Общая характеристика
- •4.2.2. Задача управления запасами при детерминированном
- •4.2.3. Задача управления многономенклатурными запасами при ограничении на емкость склада
- •4.2.4. Модель управления запасами при вероятностном спросе и мгновенных поставках
- •4.2.5. Динамические задачи управления запасами
- •5. Принятие решений в условиях неопределенности. Метод анализа иерархий.
- •5.1. Иерархическое представление проблемы
- •5.1.1. Структуризация задачи в виде иерархии
- •5.1.2. Парное сравнение альтернатив (метод парных сравнений)
- •5.1.3 Вычисление коэффициентов важности для элементов каждого уровня
- •5.1.4. Подсчет количественной оценки качества альтернатив (иерархический синтез)
- •2.2. Метод сравнения объектов относительно стандартов [2]
- •5.3. Многокритериальный выбор в иерархиях с различным числом и составом альтернатив под критериями [2]
- •5.4. Общая характеристика подхода метода анализа иерархий
- •6. Элементы теории матричных игр.
- •6.1. Игровой подход к принятию решений в условиях неопределённости.
- •6.2. Основные понятия теории игр.
- •6.3. Сведения матричной игры к задаче линейного программирования [2, 3]
- •6.4. Матричная игра двух лиц с ненулевой постоянной суммой [1]
- •Вопрос 1. Нижняя цена матричной игры определяетсяследующей формулой:
- •Вопрос 2. Верхняя цена матричной игры определяетсяследующей формулой:
- •Вопрос 4. Какова нижняя и верхняя цена игры для нижеприведенной матрицы?
- •Вопрос 5. Чему равно значение элемента матрицы игры в сед-ловой точке?
- •Вопрос 6. Используя свойство доминирования стратегий игроков, максимально редуцируйте следующую матрицу игры:
- •Вопрос 7. Найдите цену следующей игры
- •Вопрос 10. Постройте платежную матрицу следующей игры.
- •7. Теория массового обслуживания
- •3. Марковские смо.
4.2.3. Задача управления многономенклатурными запасами при ограничении на емкость склада
Рассмотрим задачу создания многономенклатурных запасов при ограничении на суммарную емкость склада.
Пусть
для і-го
вида продукта (запаса) затраты на заказ
фиксированы и составляют
![]() ,
удельные затраты на хранение единицы
продукта
,
удельные затраты на хранение единицы
продукта![]() ,
,![]() ,
спрос детерминированный с интенсивностью
,
спрос детерминированный с интенсивностью![]() ,
(i
= 1, 2, ., n). Предположим
также, что поставки выполняются мгновенно
(
,
(i
= 1, 2, ., n). Предположим
также, что поставки выполняются мгновенно
(![]() ), и дефицитне
допускается (
), и дефицитне
допускается (![]() ), причем заказы по разным продуктам
выполняются независимо. Тогда средние
общие затраты по всем номенклатурам в
единицу времени (при замене
), причем заказы по разным продуктам
выполняются независимо. Тогда средние
общие затраты по всем номенклатурам в
единицу времени (при замене![]() )
определяются соотношением
)
определяются соотношением
![]() ,
(7.3.21)
,
(7.3.21)
где
![]() -
размер заказа по
-
размер заказа по![]() -и
номенклатуре.
-и
номенклатуре.
Если
на запасы наложено ограничение, что
средний суммарный уровень не должен
превышать емкости складов, то необходимо
минимизировать
![]() при
ограничении вида
при
ограничении вида
![]() .
(7.3.22)
.
(7.3.22)
Сначала определим оптимальный размер заказа по каждой номенклатуре по формуле Уилсона (7.3.20):
![]() ,
i
= 1, 2, ., n.
(7.3.23)
,
i
= 1, 2, ., n.
(7.3.23)
Если
![]() ,
то ограничение (7.3.22) выполняется и
(7.3.23) определяет оптимальные размеры
заказов
,
то ограничение (7.3.22) выполняется и
(7.3.23) определяет оптимальные размеры
заказов![]() .
В противном случае, необходимо искать
минимум (7.3.21) при ограничении
.
В противном случае, необходимо искать
минимум (7.3.21) при ограничении
![]() (7.3.24)
(7.3.24)
Для этого применим метод множителей Лагранжа. Составим функцию
![]() .
(7.3.25)
.
(7.3.25)
Оптимальные
значения переменных
![]() определяются
решением системы уравнений
определяются
решением системы уравнений
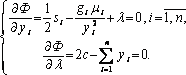 (7.3.26)
(7.3.26)
Отсюда
оптимальный размер заказа
![]() определяется
соотношением
определяется
соотношением
 .
(7.3.27)
.
(7.3.27)
4.2.4. Модель управления запасами при вероятностном спросе и мгновенных поставках
Рассмотрим некоторые задачи управления запасами при вероятностном спросе. Простейшим случаем управления запасами является однократное принятие решений на пополнение запасов [І8]. Рассмотрим этот вариант.
I
вариант.
Рассмотрим модель управления запасами
при вероятностном спросе и мгновенных
поставках. Пусть
![]() -
запас продукта к началу операции;
-
запас продукта к началу операции;![]() -
запас после пополнения (
-
запас после пополнения (![]() ),
а (
),
а (![]() ) - случайный спрос за время операции
) - случайный спрос за время операции![]() ;
;![]() -
плотность распределения спроса;
-
плотность распределения спроса;![]() -
расходы на пополнение запасов.
-
расходы на пополнение запасов.
Предположим,
что заказ на пополнение выполняется
мгновенно. Если к концу операции на
складе остается часть невостребованного
запаса
![]() ,
то система снабжения несет расходы на
сохранение избыточного запаса
,
то система снабжения несет расходы на
сохранение избыточного запаса![]() (при
(при![]() ,
,![]() ).
Наоборот, при неполном удовлетворении
спроса (
).
Наоборот, при неполном удовлетворении
спроса (![]() ) система платит штраф за дефицит
) система платит штраф за дефицит![]() .
Тогда математическое ожидание суммарных
расходов системы за период равно
.
Тогда математическое ожидание суммарных
расходов системы за период равно
![]() .
(7.3.28)
.
(7.3.28)
Найдем,
при каких значениях
![]() величина
величина![]() будет
минимальной. Для этого определим
будет
минимальной. Для этого определим
![]() ,
(7.3.29)
,
(7.3.29)
где
![]() ,
,![]() ,
,![]() -
обозначены частные производные по
соответствующим функциям ( в (7.3.29) учтено,
что
-
обозначены частные производные по
соответствующим функциям ( в (7.3.29) учтено,
что![]() ,
и положим
,
и положим![]() ).
).
В
общем случае функция
![]() при
фиксированных
при
фиксированных![]() может
иметь несколько минимумов.
может
иметь несколько минимумов.
Обозначим
через
![]() абсциссу
абсолютного минимума
абсциссу
абсолютного минимума![]() ,
а через
,
а через![]() ,
,![]() ,
,![]() точки
следующих относительных минимумов,
причем пусть
точки
следующих относительных минимумов,
причем пусть![]() <
<![]() <
<![]() <
.<
<
.<![]() (рис. 7.12). Пусть далее
(рис. 7.12). Пусть далее
![]() ,
,![]() ,
,![]() -
точки, удовлетворяющие таким
условиям:
-
точки, удовлетворяющие таким
условиям:![]() <
<![]() <
<![]() <
<![]() <.;
<.;![]() =
=![]() ,
,
![]() =
=![]() и
т.д.
и
т.д.
Тогда оптимальная стратегия управления запасами будет такой [18; 49]:
при
![]() заказывать
заказывать![]() ;
;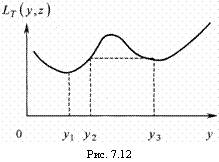
при
![]() ничего
не заказывать;
ничего
не заказывать;
при
![]() заказывать
заказывать![]() и
т.д.
и
т.д.
Приведем
достаточные условия, при которых
оптимальная стратегия имеет более
простую форму, отвечающую одному минимуму
функции
![]() [49]:
[49]:
a)![]() - не является относительным минимумом
и
- не является относительным минимумом
и
![]() ;
;
в)
уравнение
![]() имеет
не более одного вещественного корня;
имеет
не более одного вещественного корня;
c)![]() →
∞
при
→
∞
при
![]() →
∞.
→
∞.
Поясним физический смысл условий: а) экономическая целесообразность создания положительного запаса; с) неэффективность слишком больших запасов.
Обозначим
через
![]() решение
уравнения
решение
уравнения![]() (рис.
7.13). Тогда оптимальная стратегия
единственная и будет следующей:
(рис.
7.13). Тогда оптимальная стратегия
единственная и будет следующей: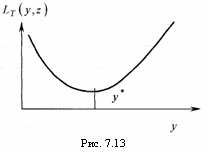
при
![]() заказывать
(делать заказа на поставку)
заказывать
(делать заказа на поставку)![]() ;
;
при
![]()
![]() ничего
не заказывать.
ничего
не заказывать.
ІІ
вариант.
Допустим, что стоимость пополнения
запасов равна
![]() при
при![]() и
нулю при
и
нулю при![]() .
Как видим, в этом случае в сравнении с
вариантом І появился дополнительный
член
.
Как видим, в этом случае в сравнении с
вариантом І появился дополнительный
член![]() (фиксированная
плата за заказ). В этом случае заказ
целесообразно делать лишь при условии
(фиксированная
плата за заказ). В этом случае заказ
целесообразно делать лишь при условии
![]() .
(7.3.30)
.
(7.3.30)
Если
уравнение (7.3.30) имеет единственное
решение
![]() ,
то оптимальная стратегия, как видно из
рис. 7.14, имеет вид [49]:
,
то оптимальная стратегия, как видно из
рис. 7.14, имеет вид [49]: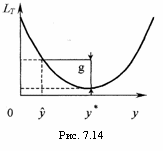
при
![]() заказывать
заказывать![]() ;
;
при
![]()
![]() ничего
не заказывать.
ничего
не заказывать.
В литературе эта стратегия называется 'стратегией двух уровней' или (S,s)-стратегией [49].
Определение
оптимальных уровней запасов
![]() при
вероятностном спросе и линейных функциях
затрат.
при
вероятностном спросе и линейных функциях
затрат.
Рассмотрим
частный случай модели при вероятностном
спросе, когда функции затрат
![]() ,
,![]() и
и![]() -линейные.
В этом случае величину
-линейные.
В этом случае величину![]() можно
определить аналитически.
можно
определить аналитически.
Действительно,
![]() ,
,
тогда
![]() ,
(7.3.31)
,
(7.3.31)
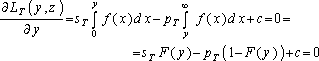
Отсюда для нахождения оптимального уровня запасов получим уравнения
![]() ;
(7.3.32)
;
(7.3.32)
где
![]() -
функция распределения случайного
спроса.
-
функция распределения случайного
спроса.
В частности, для спроса, распределенного по закону Рэлея,
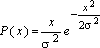 ,
,
имеем
 ,
,
отсюда
![]() .
.
Для показательного распределения спроса получим
![]() ,
,
откуда
![]() .
.
Рассмотрим
случай дискретного распределения спроса
![]() :
:
![]() (7.3.33)
(7.3.33)
Соответственно
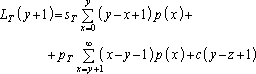 (7.3.34)
(7.3.34)
Найдем приращение
![]()
![]() .
(7.3.35)
.
(7.3.35)
Докажем
существование и единственность
оптимального решения
![]() ,
для чего исследуем знак приращения
,
для чего исследуем знак приращения![]() .
При
.
При![]()
![]() ,
,
а
при
![]()
![]() .
(7.3.36)
.
(7.3.36)
Итак,
монотонность функции
![]() обеспечивает
однократность смены знака приращения
обеспечивает
однократность смены знака приращения![]() .
Очевидно, выбор
.
Очевидно, выбор![]() должен
производиться из условий:
должен
производиться из условий:
![]() ,
(7.3.37)
,
(7.3.37)
которые можно свести к системе неравенств:
![]() .
(7.3.38)
.
(7.3.38)
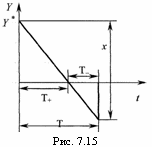
Найдем расходы за период так же, как и в детерминированном случае (рис. 7.15):
а)
при
![]()
![]() средний
положительный запас равен
средний
положительный запас равен![]() ,
а время его существования
,
а время его существования![]() ;
;
б)
при
![]() получим
средний положительный запас
получим
средний положительный запас![]() ,
средний дефицит
,
средний дефицит![]() ,
время существования запаса
,
время существования запаса![]() и
время существования дефицита
и
время существования дефицита![]() .
.
Общие расходы в единицу времени составляют
![]()
![]() .
.
