Тема 2.

Элементы линейной алгебры

Для изучения данного раздела дисциплины необходимы знания элементарной математики.

Изучив данную тему, студент должен:

• научиться работать с матричной формой представления информации, решать любые СЛАУ;

• уметь решать любые задачи линейной алгебры;

• приобрести навыки решения задач линейной алгебры с помощью пакетов прикладных программ.

Цель изучения – выработать навыки решения систем линейных алгебраических уравнений.

2.1. Алгебра матриц

2.1.1. Виды матриц

Определение: Матрицей A = (a_ij) размера m  n называется прямоугольная таблица чисел, содержащая m строк и n столбцов:

.

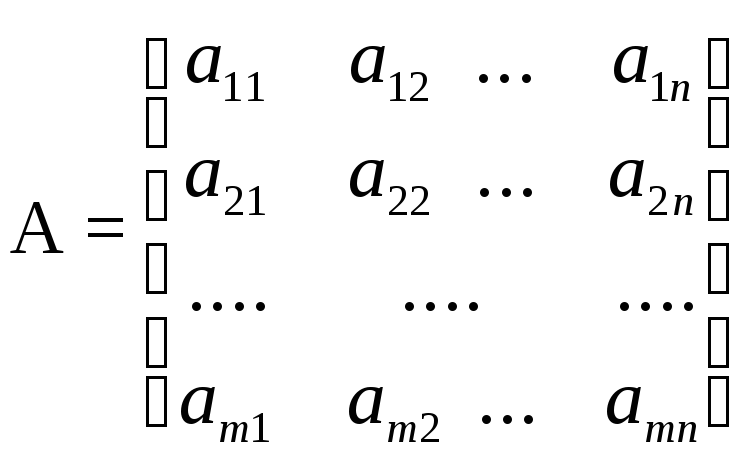Числа а_ij (I = 1...m; j = 1...n), составляющие данную матрицу, называются ее элементами: i – номер строки матрицы, j – номер столбца.

Если m = n, то матрица называется квадратной порядка n. Например, 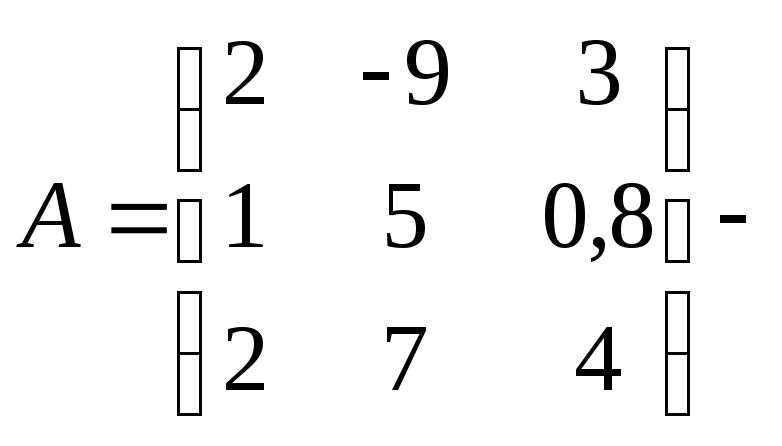квадратная матрица третьего порядка.

Матрица, состоящая из одной строки, называется вектором-строкой, а матрица, состоящая из одного столбца – вектором-столбцом. A = (a₁₁ a₁₂,…, a_1n) – вектор-строка;

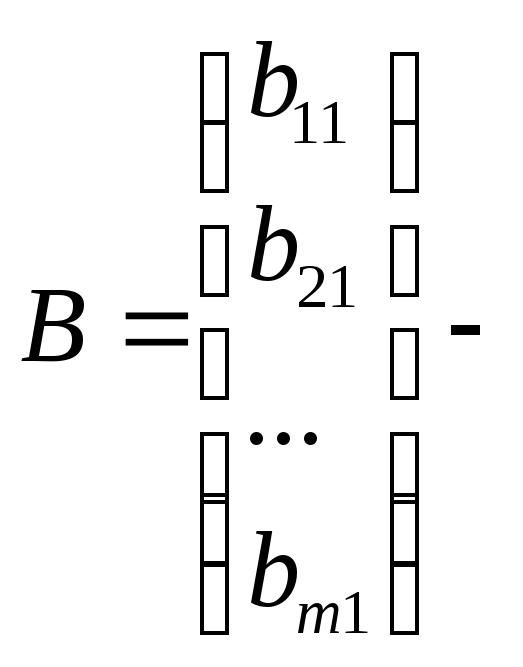вектор-столбец.

Элементы квадратной матрицы a_ij, у которых номер столбца равен номеру строки (I = j), называются диагональными и образуют главную диагональ матрицы.

Если все внедиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,

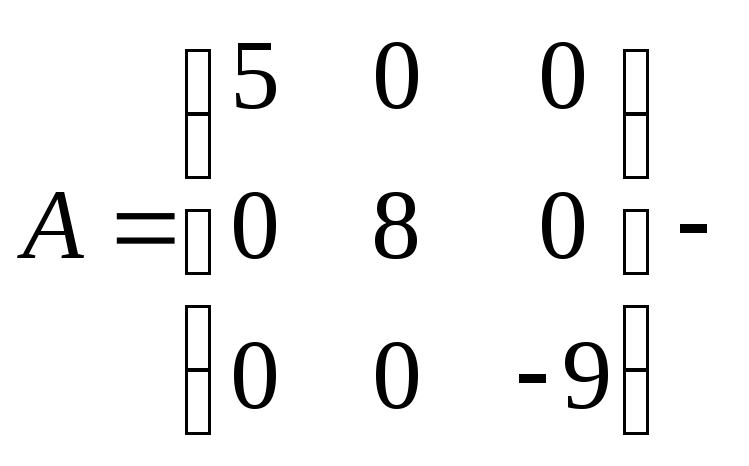диагональная матрица третьего порядка.

Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой E. Например, 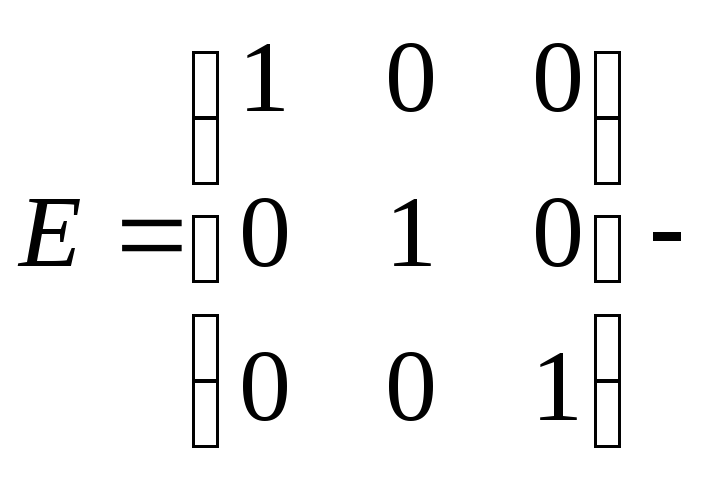единичная матрица третьего порядка.

Матрица любого размера называется нулевой, или нуль-матрицей, если все её элементы равны нулю:

.

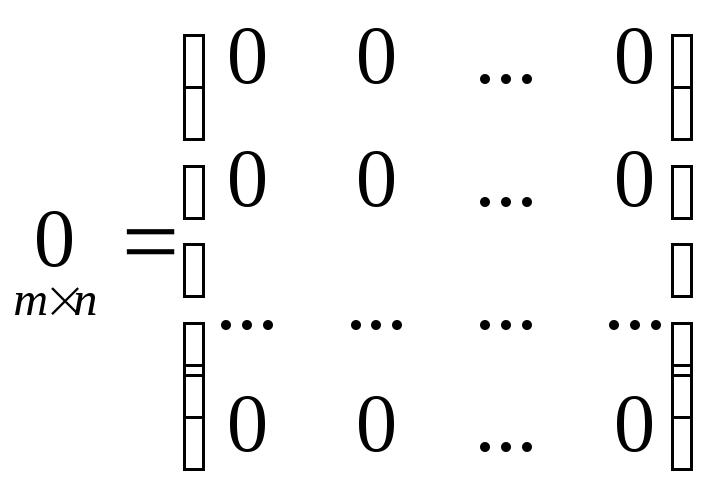Две матрицы А = (а_ij)_m,n и В = (b_ij)_m,n называются равными, если их соответствующие элементы равны, т.е. А = В тогда и только тогда, когда a_ij = b_ij, i=1...m; j = 1...n.

2.1.2. Действия над матрицами

Суммой двух матриц А = (а_ij)_m,n и В = (b_ij)_m,n называется матрица С = А + В, элементы которой с_ij равны сумме соответствующих элементов а_ij и b_ij матриц А и В.

Например: .

Для суммы матриц справедливы следующие свойства:

1. А + В = В + А – коммутативность;

2. А + (В + С) = (А + В) + С – ассоциативность;

3. А + 0 = А, 0 – нулевая матрица.

Произведением матрицы А = (а_ij)_m,n на число называется матрицаВ = А, элементы которой b_ij вычисляются следующим образом: b_ij = a_ij, i = 1...m; j = 1...n. Например, если

то .

Из определения произведения матрицы на число вытекают следующие свойства:

1. А=А4. .

2. 1  А =А 5. .

3. 0  А = 0 6. .

Определение: Матрица (-А) = (-1)  А называется противоположной матрице А.

Разность двух матриц одинакового размера определяется через предыдущие операции: A – B = A +(-1)  B.

Произведением матрицы А порядка m k на матрицу В порядка k n (т.е. количество столбцов первой матрицы равно числу строк второй) называется матрица С = А  В порядка m n , элементы которой с_ij вычисляются по формуле

с_ij = a_i1b_1j + a_i2b_2j + ... + a_ikb_ki , I = 1...m; j = 1...n.

Из данного выражения следует правило умножения матриц: чтобы получить элемент, стоящий на пересечении i-й строки и j-го столбца матрицы С, необходимо все элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Для произведения матриц справедливы следующие свойства:

1. А(ВС) = (АВ)С 3. (А+В)С = АС+ВС

2. (АВ) = (А)В 4. С (А+В) =СА+СВ

Произведение двух матриц не коммутативно, т.е. в общем случае АВ ВА. Если АВ = ВА, то матрицы А и В называются коммутативными. Так, например, единичная матрица Е коммутативна с любой квадратной матрицей того же порядка, причем АЕ = ЕА = А.

Пример 2.1. Найти произведения АВ и ВА матриц:

.

Решение:

.

Пример 2.2. Найти произведение AB двух векторов:

.

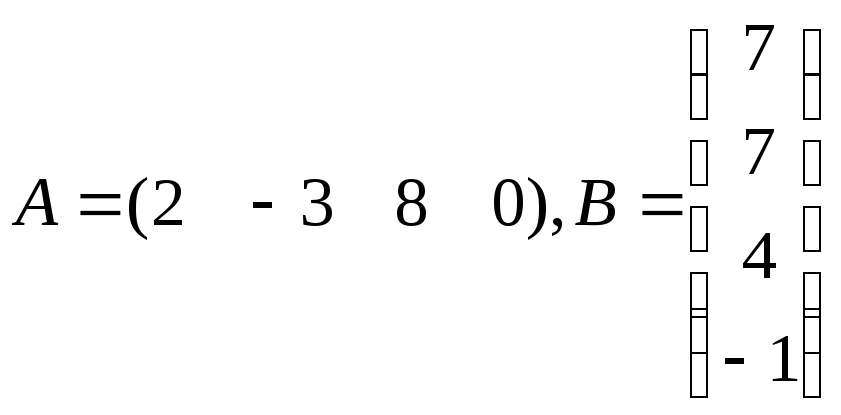Решение. При умножении матрицы-строки на вектор-столбецполучаем число:

Пример 2.3. Найти произведение KL следующих матриц:

.

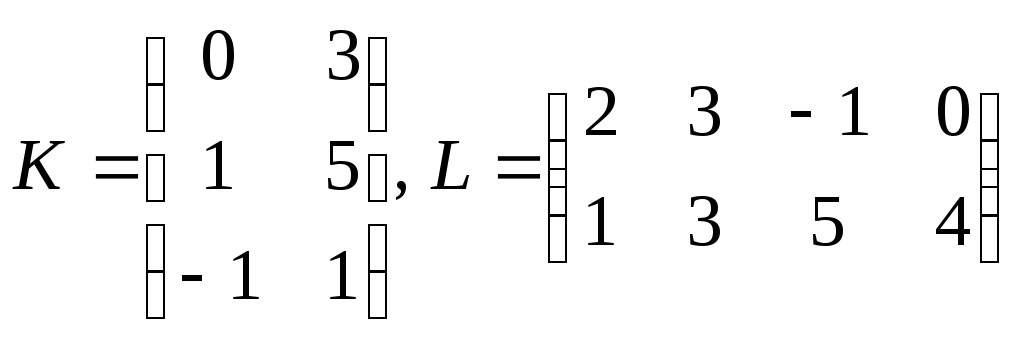Решение:

Транспонирование матрицы – это такое преобразование, при котором строки заменяются соответствующими столбцами. Обозначение транспонированной матрицы: .

Транспонированная матрица обладает следующими свойствами:

1. (А`)` = A,

2. (A + B)` = A` + B`,

3. (AB)` = B`A`.

Матрица А = (а_ij)_m,n называется симметрической, если она совпадает со своей транспонированной.

Квадратная матрица А^-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению

А^-1А = АА^-1 = Е.

Обратную матрицу можно вычислить на основании следующих элементарных преобразований (преобразований Жордана–Гаусса) над строками матрицы:

1. умножение строки матрицы на любое число, отличное от нуля;

2. прибавление к одной строке матрицы другой строки, умноженной на любое число.

Для того чтобы вычислить обратную матрицу для матрицы А, необходимо составить матрицу , затем с помощью элементарных преобразований преобразовать матрицуА к виду единичной матрицы Е, тогда на месте единичной матрицы получим матрицу А^-1.

Пример 2.4. Вычислить обратную матрицу для матрицы A:

.

Решение. Составим матрицу В⁽⁰⁾ вида

.

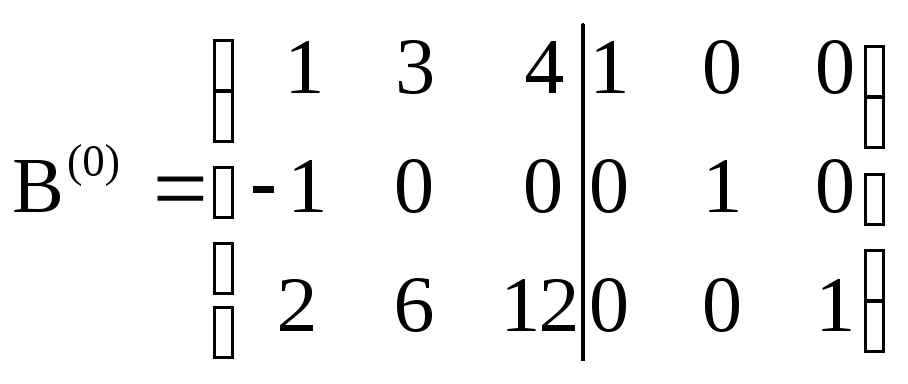Элемент и первую строку, содержащую данный элемент, назовемнаправляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный, с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и (-2). В результате данных преобразований получим матрицу

.

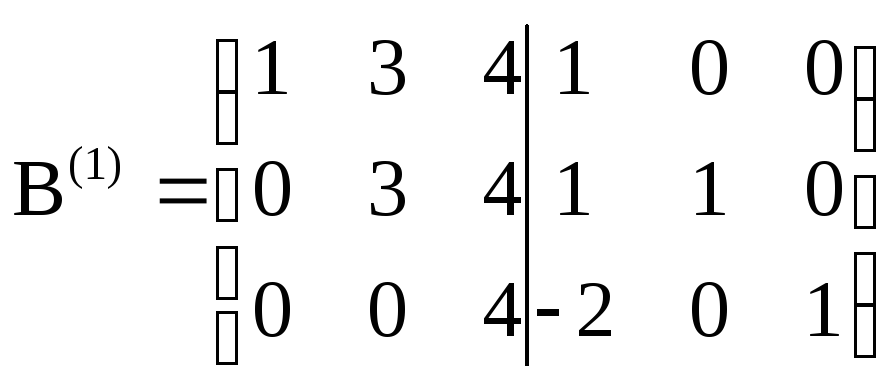В матрице В⁽¹⁾ преобразуем второй столбец в единичный. В качестве направляющего элемента выберем элемент Так как направляющий элемент, то разделим вторую (направляющую) строку на 3. Затем к первой строке прибавим вторую, умноженную на -3. Получим матрицу

.

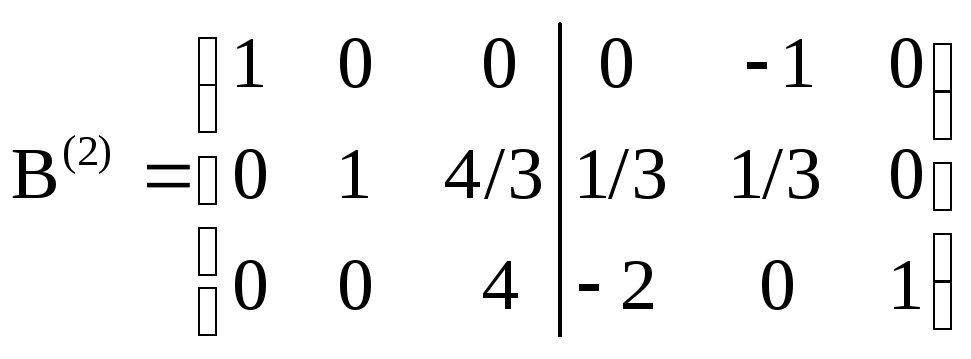Третий столбец матрицы В⁽²⁾ преобразуем в единичный. В качестве направляющего элемента выбираем Делим направляющую (третью) строку на 4 и ко второй строке прибавляем третью, умноженную на (–4/3). Получим матрицу

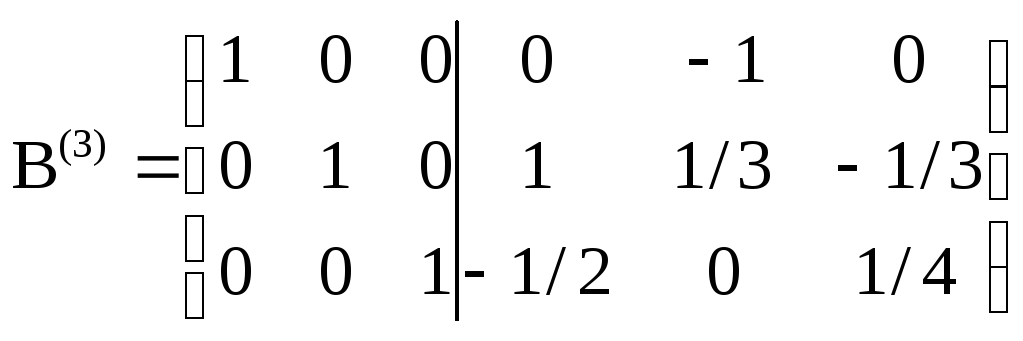
откуда

.

Выполним проверку:

Аналогично A^-1A = E.