Программное обеспечение

В математической библиотеке Matlab’а для решения краевых задач, записанных для эллиптического уравнения, имеется среда PDE Tool. Её запуск осуществляется с помощью команды

>>pdetool

из командного окна MatLab’а. В результате на экране монитора появляется окно PDE Toolbox’а, которое показано на рис.5.

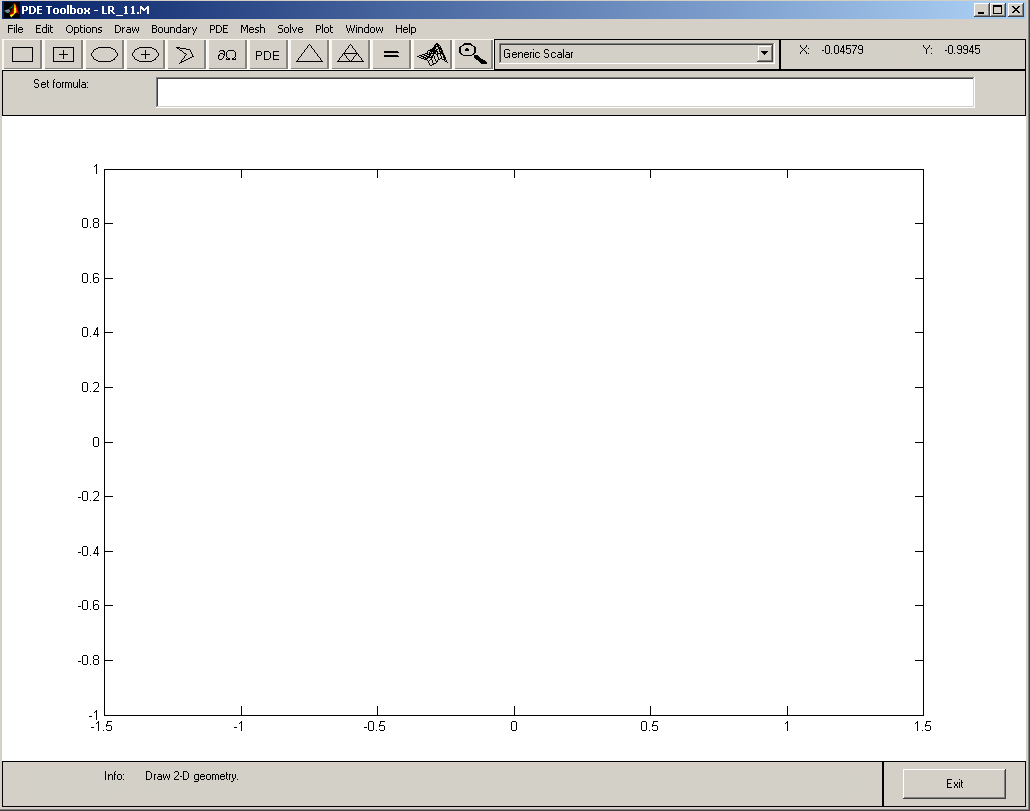
Рис.5.

Окно PDE Toolbox’а содержит следующие основные элементы:

• меню с перечнем основных операций, необходимых для решения задач;

• панель инструментов рисования геометрических примитивов, определяющих область поиска решения;

• панель инструментов для задания граничных условий, коэффициентов уравнения, построения конечно-элементной сетки, непосредственного решения задачи и визуализации полученных результатов;

• область ввода Set formulaдля конструирования области из геометрических примитивов;

• поле для построения области поиска решения с осями координат.

Настройка среды PDE Tool и процесс построения с её помощью решения краевой задачи для эллиптического уравнения показаны ниже на примере решения конкретной краевой задачи.

Пример решения на пэвм

У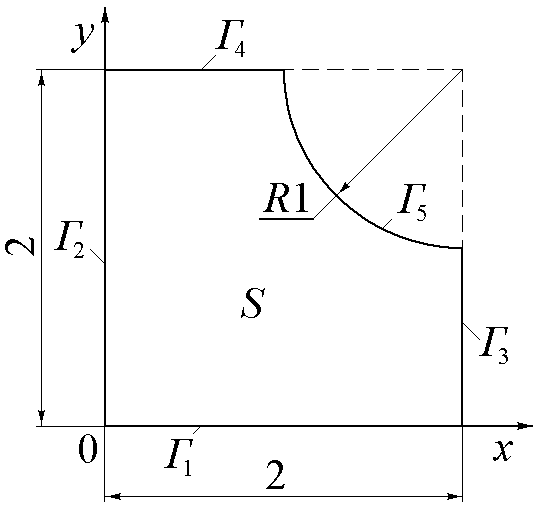словия задачи. Найти решение краевой задачи для эллиптического уравнения

,

где область S поиска решения показана на рис.6. На границе Г области S заданы следующие граничные условия

,

.

Оценить погрешность решения.

Р

Рис.6.

ешение. Настройка среды PDE Tool начинается с сохранения проекта: File–Save as–Lr_11.m. Далее из меню PDE Toolbox’а с помощью цепочки команд Options–Application–Generic Scalar устанавливается режим решения краевой задачи для одного эллиптического уравнения. После этого решение задачи строится в 6 этапов.

1. Создание системы глобальных координат. Из меню PDE Toolbox’а по цепочке команд Options–Axis Limit задаются размеры отображаемой части пространства {x, y} в виде X-axis range: [0 3] и Y-axis range: [0 3]. После этого устанавливается одинаковый масштаб по обеим осям: Options–Axis Equal и отображение координатной сетки: Options–Grid. Результат этих действий показан на рис.7.

2. Формирование области S поиска решения. Для этого по цепочке команд Draw–Rectangle/Square надо перейти в режим рисования прямоугольника (альтернатива – кнопка панели инструментов) и, устанавливая курсор в нужные точки экрана, координаты которых отображаются в правом верхнем окне построения области, нарисовать квадрат со стороной в 2 единицы. Он будет обозначен R1. Затем по цепочке команд Draw–Ellipse/Circle (centered) (альтернатива – кнопка панели инструментов) из верхнего правого угла квадрата надо нарисовать окружность с радиусом 1 который будет обозначен E1. Теперь надо удалить круг из квадрата. Для этого в окне Set formula следует набрать «R1-E1» и перейти к заданию типа решаемого уравнения по цепочке команд: PDE–PDE Mode. Результат этого показан на рис.8.

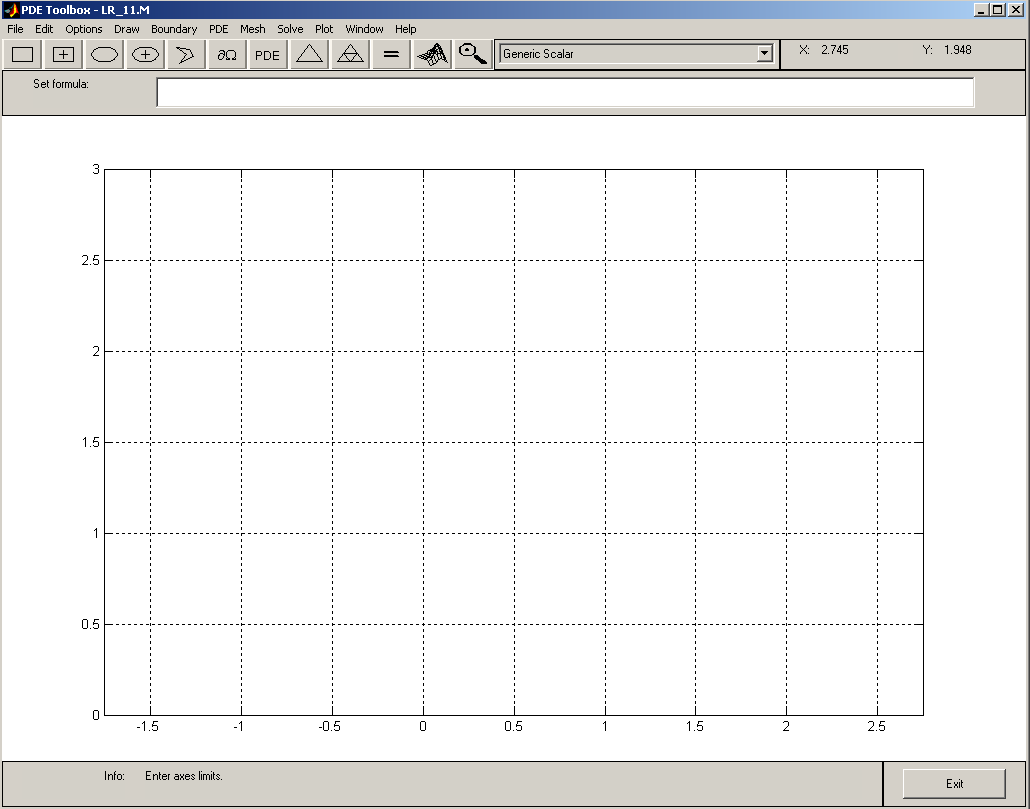
Рис.7.

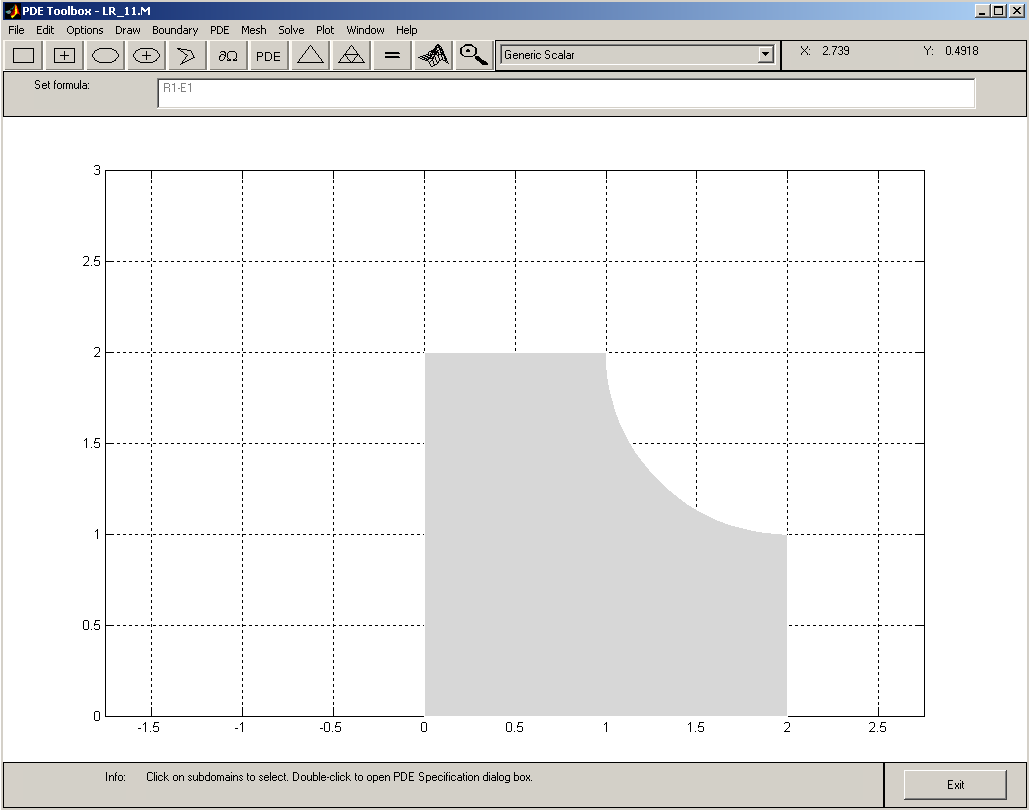
Рис.8.

3. Выбор типа уравнения и задание его коэффициентов. Сначала надо привести заданное эллиптическое уравнение к используемой в PDE Tool форме:

или

.

После этого по цепочке команд PDE–PDE Specification (альтернатива – кнопка панели инструментов) следует задать уравнение – elliptic, а коэффициенты c, a и f следующими числами и выражением: 1, -4 и 3*x.*(2-y), как показано на рис.9.

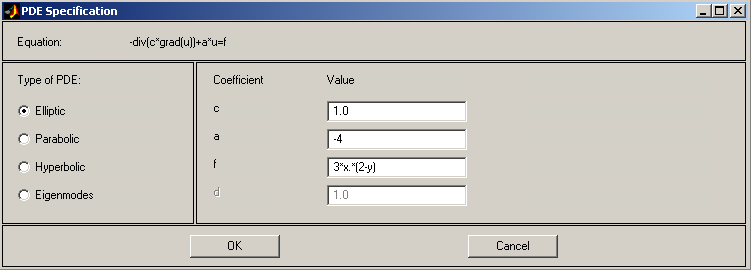
Рис.9.

4. Задание граничных условий. Здесь тоже сначала надо привести заданное граничное условие 2-го типа к используемой в PDE Tool форме:

.

Затем по цепочке команд Boundary–Show Edge Labels и Boundary–Mode следует выставить нумерацию участков границы области поиска решения 1, 2, 3, 4 и 5, иеаryчное условие 2-го типа ем: 1, -4 и 3*чю* используемому виду в 000000000000000000000000000000000000000000000000000000000000 войти в режим задания граничных условий на каждом участке границы. Этот режим предполагает активизацию левой клавишей «мыши» указанного курсором участка границы и по цепочке команд Boundary–Specify Boundary Conditions задание типа граничного условия и его коэффициентов (см. рис.10). Допускается активизация сразу нескольких участков границ при нажатой клавише Shift. Для задания на участках 1 и 2 граничного условия 1-го типа надо выбрать пункт Dirichlet и задать h и r равными 1 и 0, а для задания на участках 3, 4, 5 и 6 граничного условия 2-го типа надо выбрать пункт Neumann и задать g и q равными 4*x.*y и 2. После выполнения этого пункта алгоритма решения на экране монитора будет изображение, показанное на рис.11.

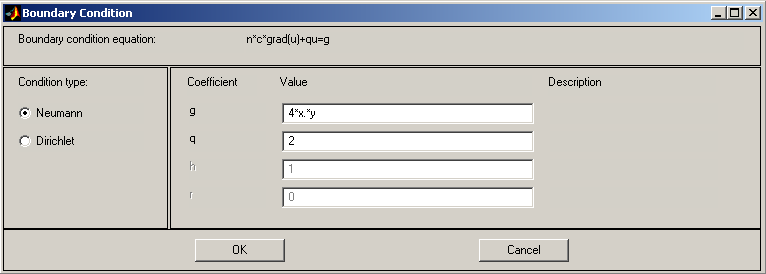
Рис.10.

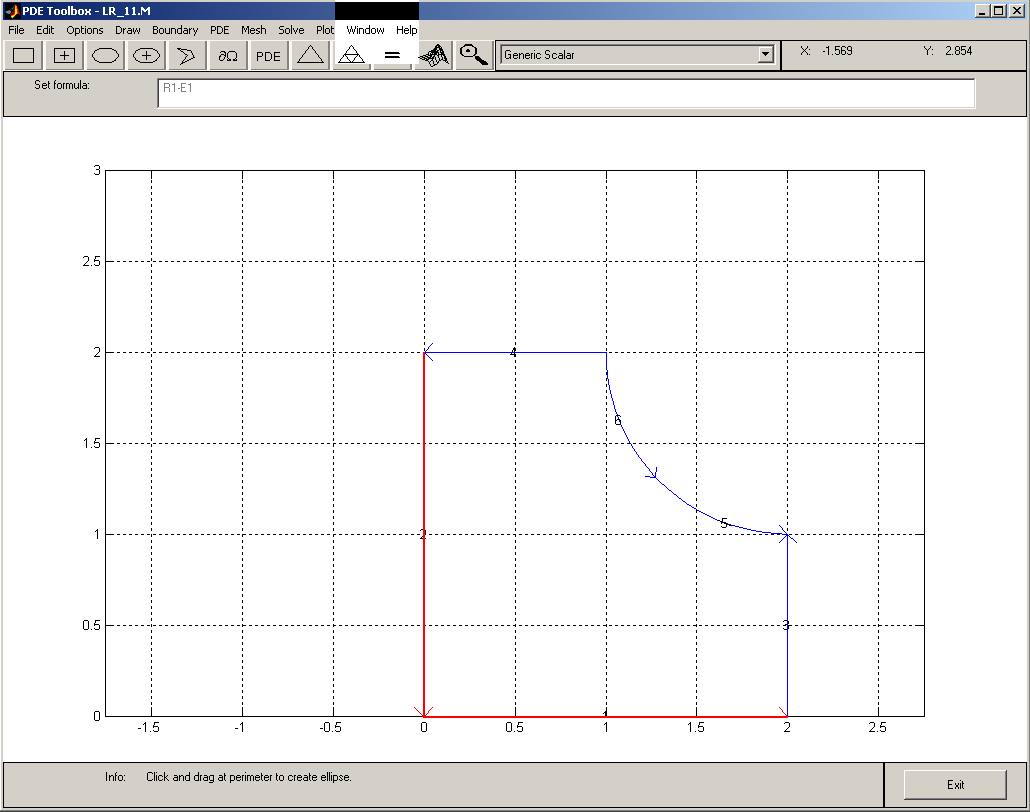
Рис.11.

5. Формирование конечно-элементной сетки. Этот этап осуществляется цепочкой команд Mesh–Initialize Mesh (альтернатива – кнопка панели инструментов). Получающаяся при этом сетка показана на рис.12. Если необходима в два раза более густая сетка, то её можно сформировать командой Mesh–Refine Mesh (альтернатива – кнопка панели инструментов).

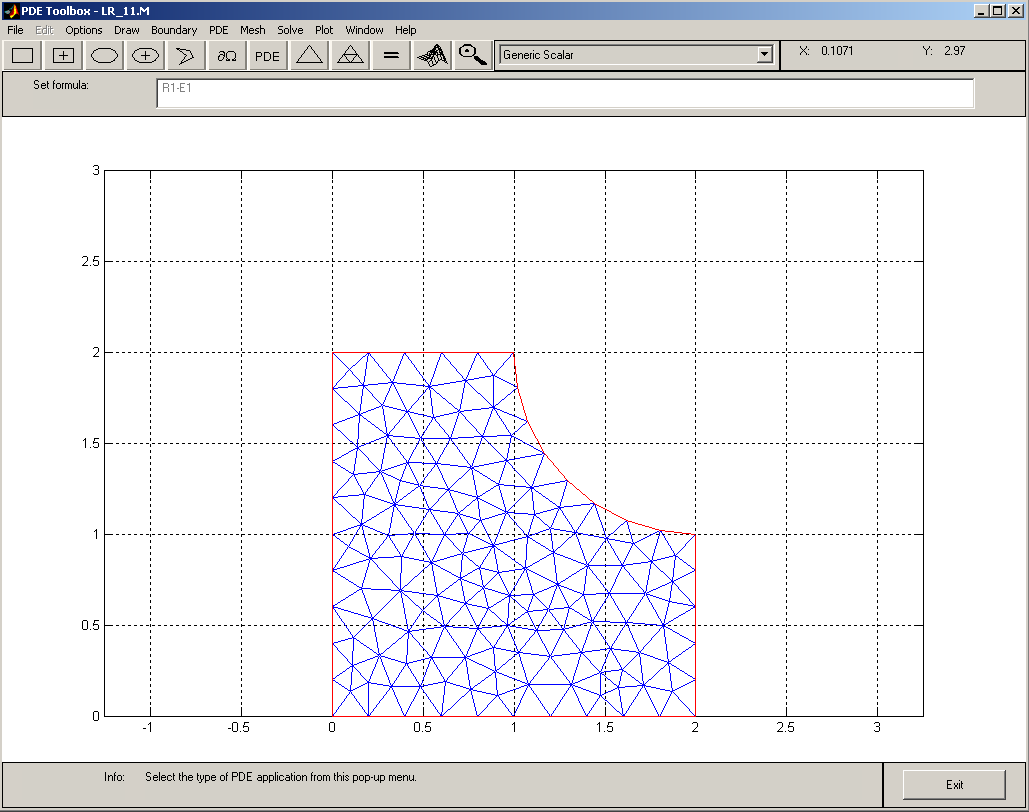
Рис.12.

6. Построение конечно-элементного решения осуществляется цепочкой команд Solve–Solve PDE. Результатом её выполнения будет цветная диаграмма, показанная на рис.13. По ней с помощью расположенной слева в окне палитры можно получить представлении о виде и величине решения u(x, y) рассматриваемой краевой задачи.

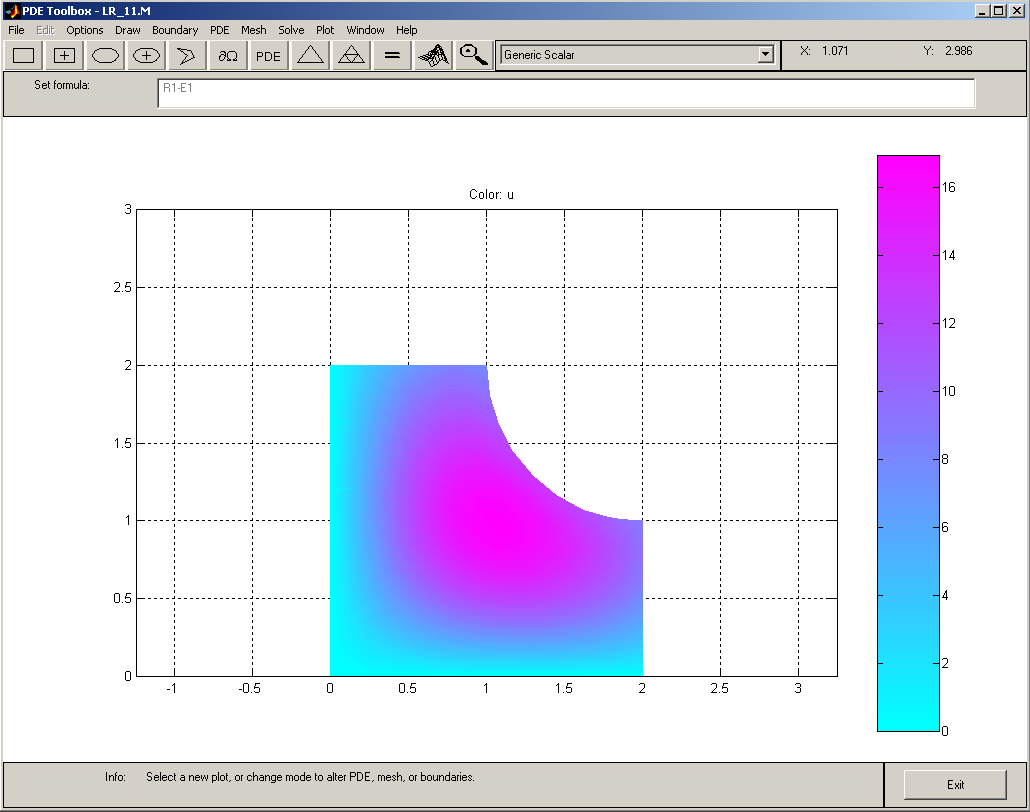
Рис.13.

В случае, когда форма представления решения не удовлетворяет каким-либо требованиям, её можно изменить. Для этого по цепочке команд Plot–Plot Solution можно попасть в меню установок визуализации решения (см. рис.14), предоставляющее пользователю широкие возможности (альтернатива – кнопка панели инструментов). Например, если кроме пункта Color активизировать ещё пункты Height(3-D plot) и Show mesh, то в графическом окне Matlab’а получится трёхмерное изображение решения, показанное на рис.15.

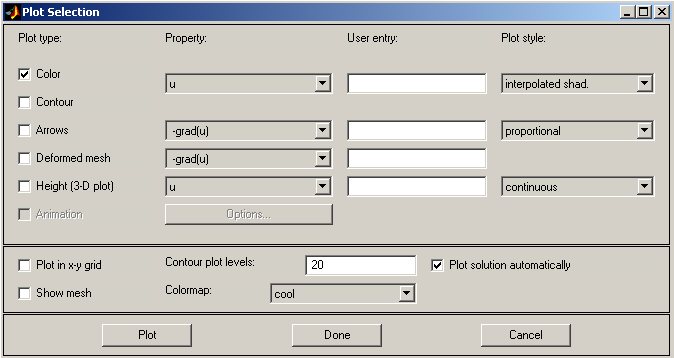
Рис.14.

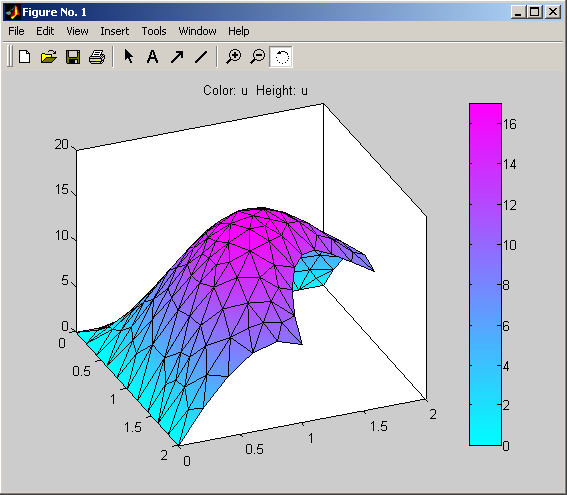
Рис.15.

Для оценки погрешности полученного решения следует воспользоваться правилом Рунге. Для этого часто достаточно снять с трёхмерного изображения, которое можно поворачивать, только наибольшее значение решения u(x, y). В данном случае оно будет равно 16.8. После этого надо повторить расчёт с более густой (в 2 раза) сеткой и опять получить наибольшее значение решения u_max = 17.2. По итогам этих замеров можно оценить погрешность более точного решения по правилу Рунге

.

По окончании работы с PDE Tool следует сохранить полученные результаты в своём наборе данных, маршрут на который должен был ранее установлен при открытии Matlab’а. Это можно сделать с помощью цепочки команд File–Save as. После этого, при необходимости, конечно-элементная модель краевой задачи может быть загружена в PDE Tool цепочкой команд File–Open.