
КР_№5_Статика
.docКонтрольная работа №5. Статика.
Содержание: 1. Задача по статике
2. Нахождение центра тяжести
3. Динамика вращательного движения
Вариант 1.
-
О
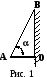 днородный
стержень АО длиной l и
массой m = 10 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол
= 60о (см. рис. 1). Определить силу
натяжения нити.
днородный
стержень АО длиной l и
массой m = 10 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол
= 60о (см. рис. 1). Определить силу
натяжения нити. -
Какой длины конец надо отрезать от однородного стержня, чтобы центр тяжести его переместился на 10 см?
-
На верёвке длиной L = 1 м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать верёвка Fmax = 80 Н. Оборвётся ли верёвка, если её отклонить на угол = 30о, а затем отпустить? На какой максимальный угол можно отклонить верёвку, чтобы она не разорвалась?
Вариант 2.
-
Ф
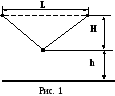 онарь
весом Р = 200 Н подвешен на тросе над
серединой улицы, ширина которой L
=10 м. Трос разрывается под действием
силы Т = 100 Н. На какой высоте Н надо
укрепить конец троса, чтобы он не
разорвался, если фонарь должен находиться
на высоте h = 6 м над
поверхностью улицы? (См. рис.1).
онарь
весом Р = 200 Н подвешен на тросе над
серединой улицы, ширина которой L
=10 м. Трос разрывается под действием
силы Т = 100 Н. На какой высоте Н надо
укрепить конец троса, чтобы он не
разорвался, если фонарь должен находиться
на высоте h = 6 м над
поверхностью улицы? (См. рис.1). -
Найти центр тяжести однородной пластины (см. рис. 2). а = 20 см, b = 30 см, с = 10 см, d = 4 см.
-
Автомобиль массой m движется по выпуклому мосту радиуса R со скоростью V. С какой силой Fд автомобиль давит на мост в точке В, находящейся под углом к вертикали? На сколько отличается эта сила от силы давления Fд1 в точке А, находящейся в середине моста? (См. рис. 3).
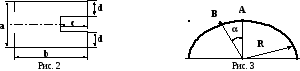
Вариант 3.
-
На балку, лежащую концами на двух опорах А и В нужно положить груз массой m = 1500 кг. Длина балки L = 7 м. На каком расстоянии от опоры А нужно расположить груз, чтобы на опору А он давил с силой F = 5000 Н?
-
И
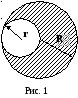 з
однородной круглой пластины радиусом
R = 9 см вырезан круг вдвое
меньшего радиуса (R = 2r),
касающийся первого круга (см. рис. 1).
Найти центр тяжести полученной пластины.
з
однородной круглой пластины радиусом
R = 9 см вырезан круг вдвое
меньшего радиуса (R = 2r),
касающийся первого круга (см. рис. 1).
Найти центр тяжести полученной пластины. -
Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, на какой высоте, считая от вершины, тело оторвётся от поверхности шара. Считать, что трение отсутствует.
Вариант 4.
-
К горизонтальному стержню длиной L = 0,4 м и весом Р = 8 Н подвешены два груза: к левому концу – груз весом Р1= 3 Н, а к правому – весом Р2= 9 Н. Определить, на каком расстоянии от левого конца надо подпереть стержень, чтобы он находился в равновесии.
-
У стены стоит лестница. Коэффициент трения лестницы о стену 1=0,4, лестницы о пол - 2=0,5. Определить наименьший угол, который может образовать лестница с полом не соскальзывая.
-
Найти максимальную разность между значениями сил натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.
Вариант 5.
-
О
 днородный
стержень АО длиной l и
массой m = 15 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол a
= 60о (см. рис. 1). Определить величину
силы реакции опоры в шарнире.
днородный
стержень АО длиной l и
массой m = 15 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол a
= 60о (см. рис. 1). Определить величину
силы реакции опоры в шарнире. -
Два однородных цилиндра, сделанных из одного и того же материала, соединены так, что оси их составляют одну прямую линию. Первый цилиндр имеет высоту h1 = 20 см и площадь сечения S1 = 9 см2, второй – h2 = 12 см и площадь сечения S2 = 5 см2. Найти центр тяжести системы.
-
На нить длиной l подвесили груз. Какую минимальную горизонтальную скорость надо ему сообщить, чтобы он сделал полный оборот в вертикальной плоскости?
Вариант 6.
-
Фонарь массой m = 20 кг подвешен на двух одинаковых тросах, образующих угол = 120о. Найти силу натяжения тросов.
-
Стержень цилиндрической формы длиной L = 40 см состоит наполовину из свинца и наполовину из железа. Плотности свинца и железа равны соответственно с = 1,14104 кг/м3, ж = 7,8103 кг/м3. Найти центр тяжести стержня.
-
Определить максимальную силу натяжения, которую выдерживает нить, к концу которой привязан шарик массой m = 500 г, если она отрывается, когда её отклоняют на угол, больший 60о.
Вариант 7.
-
К тросу длиной L = 3 м, концы которого закреплены на одной высоте, на расстоянии a = 1 м от точек закрепления, подвешены два груза массы m = 1 кг каждый. Провисание троса в средней части составило l = 10 см. Найти силы натяжения Т1, Т2 и Т3 троса на каждом из трёх участков.
-
Два шара одинакового объёма, алюминиевый и цинковый, скреплены в точке касания. Плотности алюминия и цинка равны Al = 2,7103 кг/м3 и Zn = 7,1103 кг/м3 соответственно. Найти центр тяжести системы.
-
На горизонтальном вращающемся диске, на расстоянии L = 1 м от вертикальной оси вращения лежит груз. При каком числе n оборотов в секунду груз начинает скользить, если коэффициент трения между грузом и диском равен 0,01?
Вариант 8.
-
Н
 айти
силы, действующие на стержни АВ и ВС
(см. рис. 1), если =
60о, а масса лампы m
= 3 кг.
айти
силы, действующие на стержни АВ и ВС
(см. рис. 1), если =
60о, а масса лампы m
= 3 кг. -
На конце стержня длиной L = 30 см прикреплён шар, радиус которого R = 6 см, а центр лежит на продолжении оси стержня. Где находится центр тяжести этой системы, если вес стержня и шара одинаков?
-
Маленький шарик массой m, подвешенный на невесомой нити, отклоняют от положения равновесия на угол = 60о и отпускают. Определить натяжение нити в начальный момент движения и при прохождении положения равновесия.
Вариант 9.
-
Э
 лектрическая
лампа (см. рис. 1) подвешена на шнуре и
оттянута горизонтальной оттяжкой.
Найти силу натяжения шнура АВ и оттяжки
ВС, если масса лампы 1 кг, а угол
= 60о.
лектрическая
лампа (см. рис. 1) подвешена на шнуре и
оттянута горизонтальной оттяжкой.
Найти силу натяжения шнура АВ и оттяжки
ВС, если масса лампы 1 кг, а угол
= 60о. -
Штанга, состоящая из цилиндра длиной L = 50 см и весом Р = 2кГ и двух скреплённых с ним шаров радиусами R1 = 3 см и R2 = 6 см и весом Р1 = 1,5 кГ и Р2 = 12 кГ (см. рис. 2). Найти центр тяжести штанги.
-
Два тела массами m1 и m2 находятся на стержне, по которому они могут свободно двигаться (см. рис. 3). Тела соединены нитью длиной l. Стержень вращается с угловой скоростью w относительно вертикальной оси вращения. Определить, на каком расстоянии от оси вращения установятся тела.

Вариант 10.
-
О
 днородный
стержень АО длиной l и
массой m = 20 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол a
= 60о (см. рис. 1). Определить угол
между силой реакции в шарнире и стенкой.
днородный
стержень АО длиной l и
массой m = 20 кг, расположенный
горизонтально и шарнирно закреплённый
в точке О, удерживается нитью АВ,
образующей со стержнем угол a
= 60о (см. рис. 1). Определить угол
между силой реакции в шарнире и стенкой. -
П
 ять
шаров, вес которых последовательно
равен Р1 = 1 кГ, Р2 = 2 кГ, Р3
= 3 кГ, Р4 = 4 кГ и Р5 = 5 кГ
укреплены на стержне так, что их центры
находятся на равном расстоянии друг
от друга (см. рис. 2). Пренебрегая весом
стержня, найти центр тяжести системы.
ять
шаров, вес которых последовательно
равен Р1 = 1 кГ, Р2 = 2 кГ, Р3
= 3 кГ, Р4 = 4 кГ и Р5 = 5 кГ
укреплены на стержне так, что их центры
находятся на равном расстоянии друг
от друга (см. рис. 2). Пренебрегая весом
стержня, найти центр тяжести системы. -
Определить плотность планеты, если тела на её экваторе невесомы. Период обращения планеты вокруг оси Т = 20 ч.
Вариант 11.
-
Найти силы, действующие на подкос ВС и тягу АС (см. рис. 1), если АВ = 1,5 м, АС = 3 м, ВС = 4 м, а масса груза m = 200 кг.
-
Н
 а
доске длиной L = 4 м и весом
Р = 30 кГ качаются два мальчика весом Р1
= 30 кГ и Р2 = 40 кГ. Где должна быть
у доски точка опоры, если мальчики сидят
на концах доски?
а
доске длиной L = 4 м и весом
Р = 30 кГ качаются два мальчика весом Р1
= 30 кГ и Р2 = 40 кГ. Где должна быть
у доски точка опоры, если мальчики сидят
на концах доски? -
Вычислить линейную скорость искусственного спутника Земли на высоте Н = 1700 км над поверхностью Земли, если его орбиту можно считать круговой. Принять RЗ = 6400 км, а ускорение свободного падения на поверхности Земли равным g = 9,8 м/с2.
Вариант 12.
-
Однородная доска массой m = 10 кг подпёрта на расстоянии 1/4 её длины. Какую силу, перпендикулярную доске, надо приложить к её короткому концу, чтобы удержать доску в равновесии?
-
Метровая линейка выдвинута за край стола на 1/4 длины и давит только на край стола, когда на свешивающийся конец её положили груз Р1 = 250 Г. Чему равен вес линейки? На какую часть длины надо выдвинуть линейку за край стола, если на свешивающийся конец её положить груз Р2 = 125 Г?
-
На экваторе воображаемой планеты тела весят вдвое меньше, чем на полюсе. Определить среднюю плотность вещества планеты, если период её вращения вокруг оси Т = 1 ч 27,5 мин.
Вариант 13.
-
Рельс длиной L = 10 м и массой m = 900 кг, поднимают на двух параллельных тросах. Найти силу натяжения тросов, если один из них закреплён на конце рельса, а другой на расстоянии L1 = 1 м от другого конца.
-
Б
 алка
весом Р1 = 150 кГ заделана одним
концом в стену и опирается в точках А
и В (см. рис. 1), а на другом её конце С
находится груз Р = 200 кГ. Считая, что вся
нагрузка воспринимается опорами А и
В, определить силы давления в опорах,
если СА = 1,5 м и АВ = 0,5 м.
алка
весом Р1 = 150 кГ заделана одним
концом в стену и опирается в точках А
и В (см. рис. 1), а на другом её конце С
находится груз Р = 200 кГ. Считая, что вся
нагрузка воспринимается опорами А и
В, определить силы давления в опорах,
если СА = 1,5 м и АВ = 0,5 м. -
Пуля массой m попадает в шар массой М, висящий на нити длиной l, и застревает в нём. С какой максимальной скоростью может лететь пуля, чтобы нить не оборвалась? Максимальная сила натяжения, которую выдерживает нить, равна Fн.
Вариант 14.
-
К балке массой М = 900 кг и длиной L = 5 м подвешен груз массой m = 250 кг на расстоянии L1 = 1 м от одного из концов. Балка своими концами лежит на опорах. Каковы силы давления на каждую из опор?
-
Б
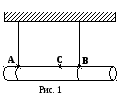 алка
весом Р = 140 кГ подвешена на двух канатах
(см. рис. 1). Какова сила натяжения этих
канатов, если расстояние АС = 3 м и СВ =
1 м? Точка С расположена в центре балки.
алка
весом Р = 140 кГ подвешена на двух канатах
(см. рис. 1). Какова сила натяжения этих
канатов, если расстояние АС = 3 м и СВ =
1 м? Точка С расположена в центре балки. -
Найти первую космическую скорость планеты, масса которой в 3 раза больше массы Земли, а радиус в 2 раза больше радиуса Земли. Принять первую космическую скорость Земли равной 8103 м/с.
Вариант 15.
-
О
 днородный
стержень АО длиной l и
массой m1 = 10 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 10 кг.
Определить силу натяжения нити АВ.
днородный
стержень АО длиной l и
массой m1 = 10 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 10 кг.
Определить силу натяжения нити АВ. -
Вагонетка весом Р = 1,5 Т имеет длину a = 3 м, а расстояние между осями b = 1,8 м. Какой силой можно приподнять вагонетку за один угол, чтобы опора оставалась на одно колесо?
-
С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом R = 40 м, чтобы пассажир на мгновение оказался в невесомости?
Вариант 16.
-
К концам стержня массой М = 10 кг и длиной 40 см подвешены грузы массами m1 = 40 кг и m2 = 10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?
-
На доске длиной 60 см стоит сплошной цилиндр, у которого высота в 3 раза больше диаметра основания. На какую наибольшую высоту можно приподнять один из концов доски, чтобы цилиндр не упал?
-
Ш
 арик
массой m, прикреплённый
к нити, движется в горизонтальной
плоскости по окружности с постоянной
скоростью (конический маятник). Расстояние
от точки подвеса до горизонтальной
плоскости равно h. Найти
период обращения шарика (см. рис. 1).
арик
массой m, прикреплённый
к нити, движется в горизонтальной
плоскости по окружности с постоянной
скоростью (конический маятник). Расстояние
от точки подвеса до горизонтальной
плоскости равно h. Найти
период обращения шарика (см. рис. 1).
Вариант 17.
-
К балке массой М = 900 кг и длиной L = 5 м подвешен груз массой m = 250 кг на расстоянии L1 = 1 м от одного из концов. Балка своими концами лежит на опорах. Каковы силы давления на каждую из опор?
-
Качели представляют собой однородную доску длиной L = 6 м, которая может качаться относительно горизонтальной оси, проходящей через центр качелей. На противоположных концах качелей сидят мальчик массы m1 = 70 кг и девочка массы m2 = 50 кг. На каком расстоянии Х от центра качелей надо положить груз массы m3 = 60 кг, чтобы качели приняли горизонтальное положение?
-
Ж
 елоб
СD, на котором лежит шарик,
образует угол =
45о с горизонтом и вращается вокруг
вертикальной оси СО 9см. рис. 1), проходящей
через нижний конец желоба. Определить,
на каком расстоянии от нижнего края
желоба шарик будет находится в равновесии
при вращении желоба со скоростью 30
об/мин. Трение не учитывать.
елоб
СD, на котором лежит шарик,
образует угол =
45о с горизонтом и вращается вокруг
вертикальной оси СО 9см. рис. 1), проходящей
через нижний конец желоба. Определить,
на каком расстоянии от нижнего края
желоба шарик будет находится в равновесии
при вращении желоба со скоростью 30
об/мин. Трение не учитывать.
Вариант 18.
-
Р
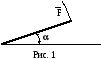 абочий
удерживает за один конец доску, масса
которой М = 40 кг так, что доска образует
угол =30о с
горизонтальным направлением (см. рис.
1). Какую силу прикладывает рабочий в
случае, когда эта сила направлена
перпендикулярно доске?
абочий
удерживает за один конец доску, масса
которой М = 40 кг так, что доска образует
угол =30о с
горизонтальным направлением (см. рис.
1). Какую силу прикладывает рабочий в
случае, когда эта сила направлена
перпендикулярно доске? -
Тонкий однородный стержень шарнирно укреплён в точке А и удерживается нитью ВС (см. рис. 2). Масса стержня m, угол его наклона к горизонту равен . Найти силу натяжения нити.
-
Г
 руз
весом Р = 0,5 кГ описывает окружность в
горизонтальной плоскости; при этом
шнур длиной L = 50 см, на
котором подвешен груз, описывает боковую
поверхность конуса и образует угол при
вершине = 60о
(см. рис. 3). Определить скорость вращения
груза.
руз
весом Р = 0,5 кГ описывает окружность в
горизонтальной плоскости; при этом
шнур длиной L = 50 см, на
котором подвешен груз, описывает боковую
поверхность конуса и образует угол при
вершине = 60о
(см. рис. 3). Определить скорость вращения
груза.
Вариант 19.
-
При взвешивании на неравноплечих рычажных весах вес тела (по сумме весов положенных гирь) на одной чашке получился равным Р1 = 2,2 кГ, а на другой Р2 = 3,8 кГ. Определить истинный вес тела Р.
-
Однородный стержень длиной L подвешен горизонтально так, что линия подвеса проходит посередине стержня. От правой части стержня отрезали кусок, составляющий 1/6 часть его общей длины, и положили на стержень, как показано на рис. 1. В какую сторону и насколько нужно переместить линию подвеса, чтобы равновесие восстановилось?
-
П
 оворот
какого радиуса может сделать автомашина,
идущая по горизонтальной дороге со
скоростью v = 43,2 км/ч, если
коэффициент трения резины об асфальт
равен = 0,2?
оворот
какого радиуса может сделать автомашина,
идущая по горизонтальной дороге со
скоростью v = 43,2 км/ч, если
коэффициент трения резины об асфальт
равен = 0,2?
Вариант 20.
-
О
 днородный
стержень АО длиной l и
массой m1 = 15 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 5 кг.
Определить величину реакции в шарнире
О.
днородный
стержень АО длиной l и
массой m1 = 15 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 5 кг.
Определить величину реакции в шарнире
О. -
О
 пределить
положение центра тяжести однородного
вала с однородным маховиком (материал
вала и маховика одинаков), если d1
= 10 см, d2 = 40 см, l1
= 100 см, l2 = 10 см, h
= 10 см. (См. рис. 2).
пределить
положение центра тяжести однородного
вала с однородным маховиком (материал
вала и маховика одинаков), если d1
= 10 см, d2 = 40 см, l1
= 100 см, l2 = 10 см, h
= 10 см. (См. рис. 2). -
Планета представляет собой однородный шар с плотностью . Каков период обращения искусственного спутника, движущегося вблизи её поверхности?
Вариант 21.
-
Однородный стержень с прикреплённым на одном из его концов грузом массой m = 1,2 кг находится в равновесии в горизонтальном положении, если его подпереть на расстоянии 1/5 длины стержня от груза. Чему равна масса стержня М?
-
К
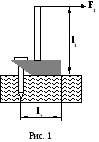 акую
силу F1 нужно
приложить к рукоятке молотка, чтобы
вырвать гвоздь (см. рис. 1), если сила
сопротивления гвоздя Fс
= 160 Н? Длина рукоятки l1
= 32 см. Расстояние от конца молотка до
гвоздя l2 = 8 см.
акую
силу F1 нужно
приложить к рукоятке молотка, чтобы
вырвать гвоздь (см. рис. 1), если сила
сопротивления гвоздя Fс
= 160 Н? Длина рукоятки l1
= 32 см. Расстояние от конца молотка до
гвоздя l2 = 8 см. -
Мост имеет форму дуги, вершина которой обращена вниз и находится на середине моста, радиус кривизны R. Масса наибольшего неподвижного груза, который может выдержать мост, m. При какой скорости v движущегося по мосту груза массой m/n (n > 1) мост разрушится?
Вариант 22.
-
Однородная балка лежит на платформе так, что один её конец свешивается с платформы. Длина свешивающегося конца балки равна четверти всей её длины. К свешивающемуся концу прилагают силу, направленную вертикально вниз. Когда эта сила становится равной F = 2000 Н, противоположный конец балки начинает подниматься. Чему равен вес Р балки?
-
О
 днородный
стержень АВ прикреплён к вертикальной
стене посредством шарнира А и удерживается
под углом = 60о
к вертикали при помощи невесомой верёвки
ВС, образующей с ним угол
= 30о (см. рис. 1). Определить силу
натяжения верёвки, а также модуль и
направление силы реакции шарнира, если
известно, что масса стержня m
= 2 кг.
днородный
стержень АВ прикреплён к вертикальной
стене посредством шарнира А и удерживается
под углом = 60о
к вертикали при помощи невесомой верёвки
ВС, образующей с ним угол
= 30о (см. рис. 1). Определить силу
натяжения верёвки, а также модуль и
направление силы реакции шарнира, если
известно, что масса стержня m
= 2 кг. -
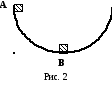
Плоское тело массой m = 4 кг движется по круговому желобу, расположенному в вертикальной плоскости (см. рис. 2). Определить силу давления тела на желоб в точке В если оно пущено с нулевой скоростью из точки А.
Вариант 23.
-
Два человека несут цилиндрическую железную трубу весом Р = 80 кГ. Один человек поддерживает трубу на расстоянии a = 1 м от её конца, а второй держит противоположный конец трубы. Определить нагрузку на каждого человека, если длина трубы l = 5 м.
-
Р
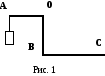 ычаг
АОВС имеет ось вращения в точке О (см.
рис. 1). Какой максимальный груз,
подвешенный в точке А, можно уравновесить
с помощью силы F = 100 Н,
приложенной в точке С, если АО:ОВ:ВС =
2:3:4? Под каким углом к горизонту должна
быть направлена сила F
чтобы удержать максимальный груз?
ычаг
АОВС имеет ось вращения в точке О (см.
рис. 1). Какой максимальный груз,
подвешенный в точке А, можно уравновесить
с помощью силы F = 100 Н,
приложенной в точке С, если АО:ОВ:ВС =
2:3:4? Под каким углом к горизонту должна
быть направлена сила F
чтобы удержать максимальный груз? -
Определить, на каком расстоянии от поверхности Земли должен находиться спутник, если он вращается в плоскости экватора с периодом, равным периоду вращения Земли вокруг оси.
Вариант 24.
-
К стене прислонена лестница весом Р. Центр тяжести лестницы находится на расстоянии 1/3 от её верхнего конца. Какую горизонтальную силу F нужно приложить к середине лестницы, чтобы верхний конец её не оказывал давления на стену? Угол между лестницей и стеной равен .
-
П
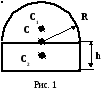 лоская
однородная фигура состоит из полукруга
радиуса R и прямоугольника
с основанием, равным диаметру полукруга
и высотой h (см. рис. 1).
Чему должно быть равно отношение R/h,
чтобы центр тяжести всей фигуры совпадал
с геометрическим центром полукруга С.
Расстояние от центра тяжести полукруга
до его геометрического центра равно
СС1 = 4R/3.
лоская
однородная фигура состоит из полукруга
радиуса R и прямоугольника
с основанием, равным диаметру полукруга
и высотой h (см. рис. 1).
Чему должно быть равно отношение R/h,
чтобы центр тяжести всей фигуры совпадал
с геометрическим центром полукруга С.
Расстояние от центра тяжести полукруга
до его геометрического центра равно
СС1 = 4R/3. -
Какова должна быть продолжительность суток на Земле, чтобы тела, находящиеся на экваторе, были в невесомости?
Вариант 25.
-
О
 днородный
стержень АО длиной l и
массой m1 = 20 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 10 кг.
Определить угол
между стержнем и силой реакции в шарнире
О.
днородный
стержень АО длиной l и
массой m1 = 20 кг,
расположенный горизонтально и шарнирно
закреплённый в точке О, удерживается
нитью АВ, образующей со стержнем угол
a = 60о (см. рис.
1). В точке А к стержню привешен груз
массой m2 = 10 кг.
Определить угол
между стержнем и силой реакции в шарнире
О. -
О
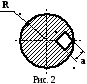 пределить
центр тяжести однородного диска с
вырезанным квадратом (см. рис. 2). Радиус
диска R, сторона квадрата
a.
пределить
центр тяжести однородного диска с
вырезанным квадратом (см. рис. 2). Радиус
диска R, сторона квадрата
a. -
К потолку трамвайного вагона подвешен на нити шар. Вагон идёт со скоростью v = 8 км/ч по закруглению радиусом R = 36,4 м. На какой угол отклонится при этом шар?
Вариант 26.
-
Стержень длиной L = 1 м и весом Р = 15 Н одним концом шарнирно прикреплён к потолку. Стержень удерживается в отклонённом положении вертикальным шнуром, привязанным к свободному концу стержня. Найти натяжение Т шнура, если центр тяжести стержня находится на расстоянии S = 0,4 м от шарнира.
-
О
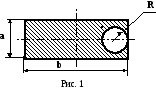 пределить
центр тяжести однородного прямоугольника
со сторонами a и b
и с вырезанным отверстием радиуса R
(см. рис. 1).
пределить
центр тяжести однородного прямоугольника
со сторонами a и b
и с вырезанным отверстием радиуса R
(см. рис. 1). -
Шоссе имеет вираж с уклоном в 10о при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?
Вариант 27.
-
Т
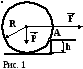 яжёлый
цилиндрический каток необходимо поднять
на ступеньку высотой h
(см. рис. 1). Определить наименьшую силу
Fмин., которую надо
приложить к центру катка в горизонтальном
направлении, если вес катка равен Р, а
радиус R (R
> h).
яжёлый
цилиндрический каток необходимо поднять
на ступеньку высотой h
(см. рис. 1). Определить наименьшую силу
Fмин., которую надо
приложить к центру катка в горизонтальном
направлении, если вес катка равен Р, а
радиус R (R
> h). -
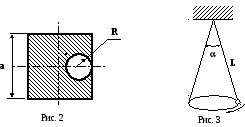
Определить центр тяжести однородного квадрата со стороной a и вырезанным отверстием радиуса R (см. рис. 2).
-
Груз весом Р = 0,5 кГ описывает окружность в горизонтальной плоскости; при этом шнур длиной L = 50 см, на котором подвешен груз, описывает боковую поверхность конуса и образует угол при вершине a = 60о (см. рис. 3). Определить силу натяжения шнура.
Вариант 28.
-
К
 вертикальной стене на верёвке подвесили
шар, причём точка подвеса находится на
одной вертикали с центром тяжести (см.
рис. 1). При каких значениях коэффициента
трения возможен такой подвес?
вертикальной стене на верёвке подвесили
шар, причём точка подвеса находится на
одной вертикали с центром тяжести (см.
рис. 1). При каких значениях коэффициента
трения возможен такой подвес? -
Определить центр тяжести однородного квадрата со стороной a и вырезанным отверстием радиуса R (см. рис. 2).
-
Г
 руз
массой m = 1 кг, висящий на
невесомом стержне длиной l
= 0,5 м, совершает колебания в вертикальной
плоскости. При каком угле отклонения
стержня от вертикали
кинетическая энергия груза в его нижнем
положении равна Wкин.
= 2,45 Дж?
руз
массой m = 1 кг, висящий на
невесомом стержне длиной l
= 0,5 м, совершает колебания в вертикальной
плоскости. При каком угле отклонения
стержня от вертикали
кинетическая энергия груза в его нижнем
положении равна Wкин.
= 2,45 Дж?
Вариант 29.
-
Лестница длиной L = 9,5 м и массой М = 16 кг приложена к гладкой вертикальной стене, а другим концом упирается в землю. Лестница составляет угол = 50о со стеной. На какое расстояние по лестнице может подняться человек массой m = 70 кг, прежде чем она начнёт проскальзывать по поверхности земли, если коэффициент трения между лестницей и землёй равен = 0,4?
-
О
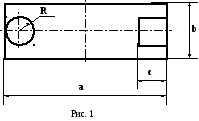 пределить
центр тяжести однородного прямоугольника
со сторонами a и b
и вырезанными, как показано на рис. 1,
отверстиями (a = 2b;
c = b/2; R
= b/4).
пределить
центр тяжести однородного прямоугольника
со сторонами a и b
и вырезанными, как показано на рис. 1,
отверстиями (a = 2b;
c = b/2; R
= b/4). -
Камень, привязанный к верёвке длиной l = 50 см, равномерно вращается в вертикальной плоскости. Найти, при каком числе оборотов в секунду верёвка разорвётся, если известно, что она разрывается при нагрузке, равной десятикратному весу камня.
Вариант 30.
-
К
 концу балки, горизонтально закреплённой
в стене, приложена сила F
=2,0 кН, направленная под углом
= 60о к горизонту (см. рис. 1).
Определить силы, изгибающие и сжимающие
балку. Вес балки равен Р = 5,0 кН.
концу балки, горизонтально закреплённой
в стене, приложена сила F
=2,0 кН, направленная под углом
= 60о к горизонту (см. рис. 1).
Определить силы, изгибающие и сжимающие
балку. Вес балки равен Р = 5,0 кН. -
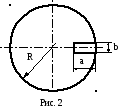
Н
 айти
центр тяжести однородной фигуры,
изображённой на рис. 2, если a
= 3b; R = 2r = 2/3 b.
айти
центр тяжести однородной фигуры,
изображённой на рис. 2, если a
= 3b; R = 2r = 2/3 b. -
Камень, привязанный к верёвке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжением верёвки равна 1 кГ.
Вариант 31.
-
О
 днородный
стержень АВ опирается о шероховатый
пол и гладкий выступ С (см. рис. 1). Угол
наклона = 45о.
Определить, чему должно быть отношение
АС/ВС, чтобы стержень находился в
равновесии. Коэффициент трения
= 0,4.
днородный
стержень АВ опирается о шероховатый
пол и гладкий выступ С (см. рис. 1). Угол
наклона = 45о.
Определить, чему должно быть отношение
АС/ВС, чтобы стержень находился в
равновесии. Коэффициент трения
= 0,4. -
Определить центр тяжести однородного диска радиуса R с вырезанным прямоугольником со сторонами a = R/2, b = R/4 (см. рис.2).
-
Ч
 еловек
массы m = 70 кг качается на
качелях. Длина верёвок, поддерживающих
сиденье качелей равна L
= 8 м. При качании человек проходит
положение равновесия со скоростью v
= 6 м/с. Какова сила натяжения Т каждой
верёвки в этот момент?
еловек
массы m = 70 кг качается на
качелях. Длина верёвок, поддерживающих
сиденье качелей равна L
= 8 м. При качании человек проходит
положение равновесия со скоростью v
= 6 м/с. Какова сила натяжения Т каждой
верёвки в этот момент?
Вариант 32.
-
На двух параллельных, вертикально расположенных пружинах одинаковой длины горизонтально подвешен стержень, весом которого можно пренебречь. Коэффициенты упругости пружин равны соответственно к1 = 0,02 Н/м и к2 = 0,03 Н/м. Расстояние между пружинами L = 1 м. В каком месте стержня нужно подвесить к груз Р, чтобы стержень оставался горизонтальным?
-
Однородный цилиндр, лежащий на горизонтальном столе, выступает за край стола на 1/6 часть своей длины. Определить вес цилиндра, если для подъёма его за тот конец, который лежит на столе, необходимо приложить силу F = 120 Н, направленную вверх. Какая сила необходима для подъёма цилиндра за другой конец?
-
Груз массой m = 1 кг, висящий на невесомом стержне длиной l = 0,5 м, совершает колебания в вертикальной плоскости, причём кинетическая энергия в его нижнем положении равна Wкин. = 2,45 Дж. Чему равен угол отклонения стержня в этом случае? Во сколько раз при таком угле отклонения натяжение стержня в его среднем положении больше натяжения стержня в его крайнем положении?
Вариант 33.
-
О
 днородный
шар массой m и радиусом
R висит, как показано на
рис. 1. Расстояние от точки крепления
нити к стене до точки касания шара равно
2R. Определить силу
натяжения нити Т и силу реакции стены
N.
днородный
шар массой m и радиусом
R висит, как показано на
рис. 1. Расстояние от точки крепления
нити к стене до точки касания шара равно
2R. Определить силу
натяжения нити Т и силу реакции стены
N. -
Тонкий однородный стержень укреплён в точке А и удерживается нитью ВС (см. рис. 2). Масса стержня m, угол его наклона к горизонту . Найти модуль и направление силы реакции шарнира.
-
Груз весом Р = 0,5 кГ описывает окружность в горизонтальной плоскости; при этом шнур длиной L = 50 см, на котором подвешен груз, описывает боковую поверхность конуса и образует угол при вершине a = 60о (см. рис. 3). Определить центростремительную силу.

Вариант 34.
-
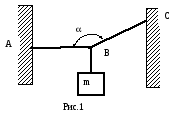
Груз массой m = 0,50 кг подвешен в точке В к нитям АВ и ВС (см. рис. 1), таким образом, что нить АВ горизонтальна, а ВС образует с нитью АВ угол = 150о. Найти величину сил натяжения нитей АВ и ВС.
-
П

 ять
шаров, вес которых последовательно
равен Р1 = 1 кГ, Р2 = 2 кГ, Р3
= 3 кГ, Р4 = 4 кГ и Р5 = 5 кГ
укреплены на стержне весом Р6 = 6 кг так,
что их центры находятся на равном
расстоянии друг от друга (см. рис. 2).
Найти центр тяжести системы.
ять
шаров, вес которых последовательно
равен Р1 = 1 кГ, Р2 = 2 кГ, Р3
= 3 кГ, Р4 = 4 кГ и Р5 = 5 кГ
укреплены на стержне весом Р6 = 6 кг так,
что их центры находятся на равном
расстоянии друг от друга (см. рис. 2).
Найти центр тяжести системы. -
На невесомый несжимаемый стержень подвесили груз. Какую минимальную горизонтальную скорость надо сообщить грузу, чтобы он сделал полный оборот в вертикальной плоскости?
Вариант 35.
-
К
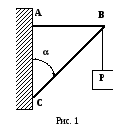 прямоугольному кронштейну АВС в точке
В подвешен груз Р = 1200 Н (см. рис. 1).
Определить силу, растягивающую
горизонтальную тягу АВ и силу, сжимающую
подкос ВС, если подкос образует угол
= 45о с вертикалью. Вес тяги и
подкоса не учитывать.
прямоугольному кронштейну АВС в точке
В подвешен груз Р = 1200 Н (см. рис. 1).
Определить силу, растягивающую
горизонтальную тягу АВ и силу, сжимающую
подкос ВС, если подкос образует угол
= 45о с вертикалью. Вес тяги и
подкоса не учитывать. -
Определить положение центра тяжести системы двух шаров, насаженных на невесомый стержень так, что расстояние между их центрами равно L.
-
Автомобиль массой m движется по мосту радиуса R со скоростью v. С какой силой Fд автомобиль давит на мост в точке В, находящейся под углом к вертикали? На сколько отличается эта сила от силы давления Fд1 в точке А, находящейся в середине моста. Мост вогнутый (см. рис. 2).
