1. Задачи математической статистики. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативная выборка. Две интерпретации выборки.

Задача: создание методов сбора и обработки стат данных с целью получ научных и практических выводов.

Цели:

1) Оценка неизвестной вероятности событий.

2)Оценка неизвестной ф-ции распределения.

3)Оценка параметров известного распределения.

4)Оценка степени зависимости одной величины от другой.

5)Проверка статистич гипотез о виде неизвестного закона распред-я.

Генеральная совокупность- мн-во объектов, из которых производится выборка. Каждый объект хар-ся некоторым кол-вом признаков, значение которых может меняться от объекта к объекту. Выборочная совокупность (Выборка)- совокупность случайно отобранных объектов.

Повторная выборка- сов-сть, при которой отобранный объект возвращается в генеральную сов-сть перед выбором следующего.

Бесповторная выборка- сов-сть, при которой отобранный объект не возвращается в генер-ю перед выбором следующей.

Репрезентативная -1) Если выборка правильно отражает пропорцию генер-й сов-сти -2) осуществить случайно и -3) каждый объект генер-й сов-сти имеет одинаковую вероятность попасть в выборку.

2 Интерпретации выборки.

Пусть в генер-й сов-сти извлечена выборка объемом n, тогда эту выборку можно интерпретировать двумя способами: 1) Практический вариант. Под 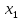…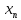понимаются наблюдаемые в данном эксперименте значения исслед-й случ величины х. 2) Гипотетический вариант. Под величинами х1..хn понимается лишь обозначение тех n значений случ величины, которые мы могли бы получить. В такой интерпретации х1 и хn случайный выбор. Причем закон распределения каждой его компоненты один и тот же и совпадает с законом распределения случайной величины х. f(x₁)=f(x₂)..=f(x).

2. Стат оценки параметров распредел. Несмещённые, эффективные и состоятельные оценки.

Стат оценка неизв параметра теоретического распределения – ф-ция от наблюдаемых случайных величин. Х – С.В. ; f (x, ) – плотность распределения, где 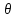- вектор параметра распределения.

f(x,m,σ) = A*(σ)*, гдеm, σ – параметры, у которых ззнач и св-ва неизвестны.

Исследовать все эл-ты генеральной совокупности для опр – нельзя. Поэтому векторусудят по выборке.

Стат оценка вектора параметра распределения - ф-ция результата набл, с помощью которой судят о знач вектора параметра

(1) X̅_в =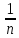∑X_i

(2) X̅_в =

Р – м мн-во выборок, объемом n. Каждая выборочная оценка параметра по i –ой выборке будет обозначаться ^*_i – С.В. , т.к. состав кождой выборки – случаен.

Св-ва оценок.

1. Несмещенность

Оценка * …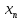– несмещенная, если при любом объеме выборкеn результат ее осреднения по всем возможны выборкам данного объема, приводит к истинному значению оцениваемого параметра. M[*] =

Характеризует оценку до асимптотического св-ва, т.е. хорошие или плохие св-ва при конечном объеме выборки.

Стат оценка * (…) – несмещенная, если ее мат ожидание = оцениваемому параметрупри любом объеме выборки, т.е.M[*] =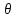

2. Эффективность

Стат оценка * (…) –- эффективная, если при заданном объеме выборки оценка имеетmin D (дисперсия – разброс вокруг среднего значения). D(Х)=М[Х-М(Х)]² - мат ожидание кВ отклонения С.В. от ее мат ожидания.

3. Состоятельность (при большом n)

Стат оценка * (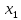…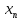) – состоятельная, если приn ∞ , оценка  по вероятности к истинному знач .

* …)--------