33.Линейная модель механизма поиска по технологии обратной связи по релевантности терминов.

Обратная связь по релевантности терминов должна обеспечить пользователю возможность целенаправленно изменять поисковый запрос путем повышения роли одних и понижения роли других терминов.

Рассмотрим диалоговую модель механизма поиска по обратной связи, предлагаемую в ИПС IRBIS. Она отличается от модели эвристического поиска тем, что после выполнения системой очередного шага пользователю предоставляется возможность управлять дальнейшим процессом формирования результата

Шаг 1. Построение и ранжирование словника релевантных документов.

Рез-том этого шага является вектор где k – количество терминов релевантных документов, а w_i - значение весового коэффициента для i-го термина, удовлетворяющее неравенству .

По завершении первого шага система передает управление пользователю, который самостоятельно отмечает термины, способные улучшить поисковый запрос.

Отмеченные термины пользователь могут самостоятельно добавить в поисковый запрос (для реализации моделей поиска по совпадению терминов или по логическому выражению) или инициировать второй шаг поиска по обратной связи.

Шаг 2. Формирование матрицы поисковых результатов.

Термины, отобранные пользователем на предыдущем шаге, рассматриваются как исходные для проведения поиска по совпадению терминов. Модель этого механизма поиска реализована построением подматрицы запроса (L_q), в которой отдельные строки могут быть нулевыми.

Рассмотрим подматрицу L_q как исходную для проведения процедуры поиска аналогов и последовательно для каждого ненулевого столбца построим вектор Q_i – результат поиска аналогов с max-ым порогом близости (задается количеством единиц в столбце, а контекст результата задается перечислением самих терминов). Полученные векторы рассмотрим как строки матрицы поисковых результатов:

,где n – количество ненулевых столбцов подматрицы L_q.

Каждая строка матрицы снабжается контекстом-перечислением конкретных терминов, присутствующих в документах конкретного результата. Матрица результатов дает возможность просматривать каждый отдельный результат, что позволяет формировать новое множество релевантных документов.

34.Матрицы ассоциации документов, терминов и их свойства.

Используем понятие универсального словаря D (прообразом которого может быть, например, тезаурус, рубрикатор), содержащего множество лексических единиц всего потока доку­ментов (то есть все слова, числа и прочие обозначения, использованные во всех документах системы). Таким образом, li принадлежит D для всех i, где li— совокупность лексических единиц некоторого документа (сообщения), который является элементом некоторого потока L: L={l1 ,...,li,..., ln}, li L для всех i

Уни­версальный массив L₀ (ИМЕТЬ В ВИДУ, НО ЛУЧШЕ НЕ ПИСАТЬ: прообразы — поисковый массив ИПС, отраслевой справочно-информационный фонд, массив библио­теки), подмножеством которого являются все документы:

L₀ = {l1 ,...,li,..., l n₀}, li L₀ для всех i, причем | L₀| = n₀, где n₀, — мощность множества L₀. Линейное представление теоретико-множественного образа документа:

l_k=, гдеb_ik= 1-если i-й термин входит в k-й документ;0- если не входит.

Универсальный массив в линейном представлении есть мат­рица размерности D х n₀ :

Подобные матрицы известны под названием матрицы «тер­мин—документ». Каждый столбец матрицы соответствует доку­менту и описывает множество терминов, содержащихся в нем.Таким образом, столбец матрицы характеризует ПОД. Строка матрицы соответствует отдельному термину и являет­ся перечнем документов, содержащих данный термин. Сумма элементов строки представляет собой частотную характеристику термина: F_i=∑b_ik.

Составим матрицу , где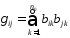.Матрицаимеет размерность. Внедиагональный элемент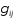есть количество появленийi-го и j-го терминов в , диагональный –i-го. Матрицы такого типа называют «матрица термин-термин» и характеризуют взаимосвязь терминов в данном массиве.

Составим матрицу L₀^T x L0 = (δ_km), δ_km=. Размерность n₀ x n₀, внедиагональные элементы характеризуют степень попарных пересечений сообщений из L₀:

Диагональные элементы задают длины сообщений:

В целом задает распределения пересечений документов и их длин.