Лабораторная работа №5

Методы интерполяции данных

Цель лабораторной работы: В рамках данной лабораторной работы необходимо исследовать различные методы интерполяции данных.

Теоретическая часть

Интерполяция - отыскание промежуточных значений величины по некоторым известным её значениям.

Линейная интерполяция (linear)— интерполяция алгебраическим двучленом

P₁(x) = ax + bфункцииf, заданной в двух точкахx₀иx₁отрезка[a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

Геометрическая интерпретация

Геометрически это означает замену графика функции fпрямой, проходящей через точки (x₀,f(x₀)) и (x₁,f(x₁)).

График: пример линейной интерполяции

Уравнение такой прямой имеет вид:

отсюда для

Это и есть формула линейной интерполяции, при этом

где R₁(x) — погрешность формулы:

Справедлива оценка

Применение

Линейная интерполяция применяется для уплотнения таблиц.

Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона.

Интерполяция методом ближайшего соседа (nearest)— самый простой метод интерполяции функции одной или нескольких переменных. В качестве интерполированного значения выбирается ближайшее известное значение функции.

Сплайн (spline)- кусочно-заданная функция, совпадающая с функциями более простой природы на каждом элементе разбиения своей области определения.

Классический сплайн одной переменной строится так: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна.

Интерполяционный многочлен Лагранжа (Lagrange)— многочлен минимальной степени, принимающий данные значения в данном наборе точек. Дляn+ 1 пар чисел, где всеx_iразличны, существует единственный многочленL(x) степени не болееn, для которогоL(x_i) =y_i.

В простейшем случае (n= 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки

Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы y_j l_j(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных x_i

Лагранж предложил способ вычисления таких многочленов:

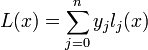
где базисные полиномы определяются по формуле:

l_j(x) обладают следующими свойствами:

• являются многочленами степени n

• l_j(x_j) = 1

• l_j(x_i) = 0 при

Отсюда следует, что L(x), как линейная комбинацияl_j(x), может иметь степень не большеn, иL(x_j) =y_j

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значенияy_j=f(x_j) в некоторых точках. Тогда мы можем интерполировать эту функцию как

В частности,

Значения интегралов от l_jне зависят отf(x), и их можно вычислить заранее, зная последовательностьx_i.