6. Криволинейный интеграл первого рода

Пусть на плоскости дана непрерывная простая спрямляемая кривая , вдоль которой расположены массы, причём известна их линейная плотностьво всех точкахкривой. Требуется определить массувсей кривой.

С этой целью разобьём кривую на отрезки точками , причем начальная точка кривой,  конечная точка;  длина -го отрезка кривой. Фиксируем произвольно точкуна отрезкеи будем считать, что плотностьсохраняет свое значение во всех точках отрезка.

Тогда масса отрезка ,

а масса всей кривой

Погрешность последнего выражения будет стремиться к нулю, если длины всех отрезков стремятся к нулю. Обозначив черезнаибольшую из длин, точное значение массы кривой получим в результате предельного перехода:

.

Отвлекаясь от задачи о массе кривой, можно рассмотреть функцию точки , заданную на кривой, и повторив рассуждения, аналогичные проведенным выше, получить интегральную сумму:

. (6.1)

Определение. Конечный предел , если он существует для любого разбиения кривойна отрезкии не зависит от выбора точек, называется криволинейным интегралом первого рода от функциипо кривойи обозначается символом

. (6.2)

(Здесь есть длина дуги кривой, а «дифференциал дуги».)

Криволинейный интеграл первого рода по пространственной кривой определяется аналогично:

. (6.3)

Свойства криволинейного интеграла первого рода

1. Криволинейный интеграл первого рода не зависит от выбора направления на пути интегрирования:

;

2. ;

3. .

4. Если путь интегрирования 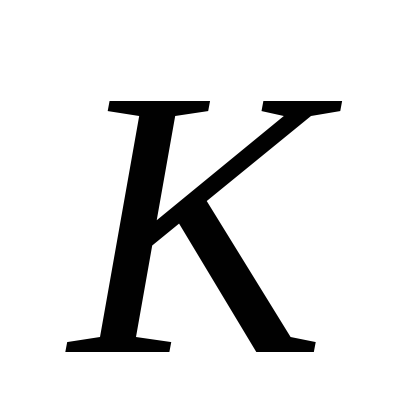разбит на части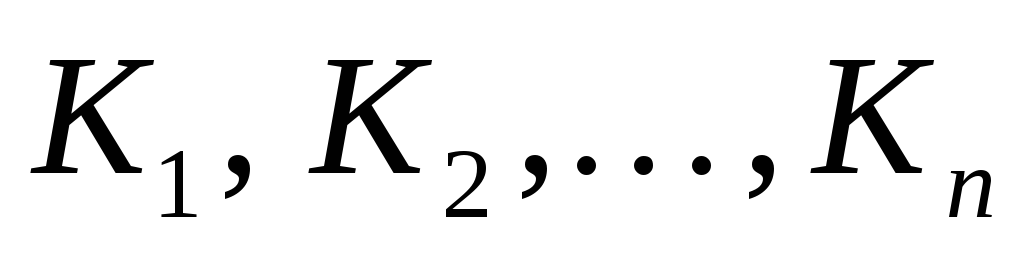, то

.

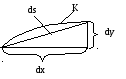
Рис. 6.1

Дифференциал дуги приближенно можно выразить в соответствии с теоремой Пифагора (рис. 6.1):



для случая кривой , принадлежащей плоскости, или



для трёхмерного случая. При эти выражения становятся точными.

Пусть кривая задана в параметрической форме:

,

причём, функции инепрерывны вместе со своими производнымии, то есть кривая гладкая или кусочно-гладкая. Если кратных точек на кривой нет, она спрямляемая. Криволинейный интеграл (6.2) существует, если подынтегральная функция  непрерывная.

Дифференциал дуги в этом случае имеет следующий вид:

.

Подставив в интеграл (6.2), получим:

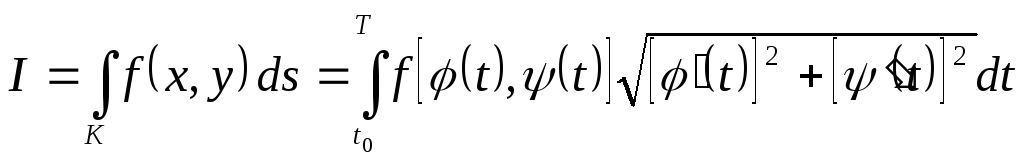. (6.4)

В случае кривой , заданной явным уравнением в декартовых координатах

,

формула (6.2) принимает вид:

. (6.5)

Пусть кривая задана в полярных координатах:

,

тогда:

,

.

Следовательно, дифференциал дуги

,

а интеграл (6.2) принимает вид

.

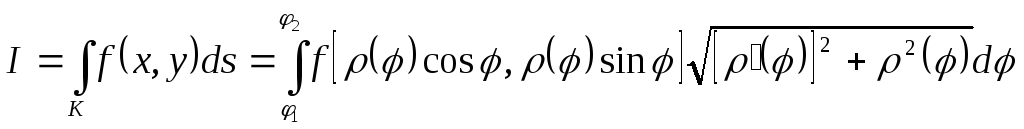Пример 6.1. Вычислить интеграл:

,

если  отрезок прямой между точками и.

Решение. Направляющий вектор прямой  .

Уравнение прямой 

или .

Дифференциал дуги 

.

.

Пример 6.2. Вычислить интеграл

,

если есть дуга окружности

,

принадлежащая первой четверти (рис. 6.2).

Решение.

.

Рис. 6.2

Подставим найденные выражения в интеграл и вычислим его:

.

Пример 6.3. Вычислить длину первой арки циклоиды:

.

(Циклоида представляет собой траекторию точки катящегося колеса, изображенную на рис. 6.3.)

Решение. Длину кривой можно найти, вычислив криволинейный интеграл

.

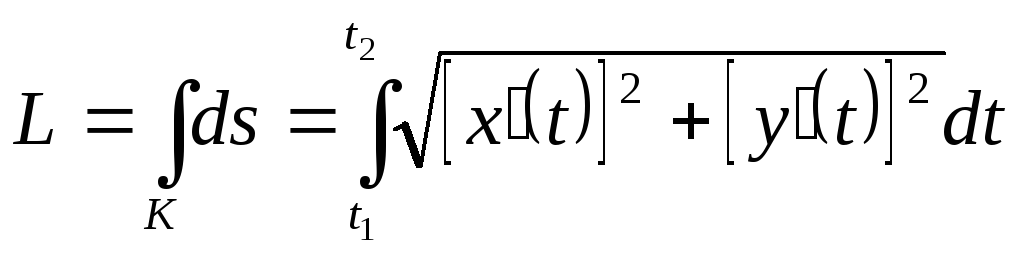Рис. 6.3

Подставив в интеграл производные

получим:

.

Пример 6.4. Вычислить длину винтовой линии, заданной уравнениями

.

Решение.

.

.

Пример 6.5. Вычислить длину спирали Архимеда (рис.6.4).

от до.

(Угол здесь выражен в радианах).

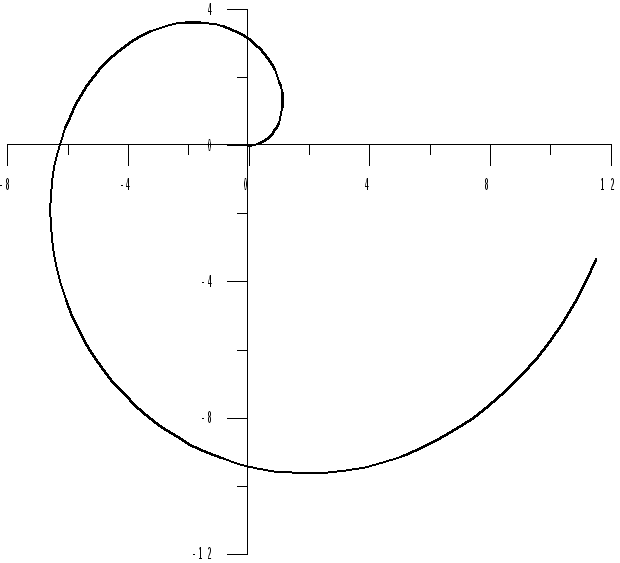
Рис. 6.4

Решение.

.

Первый интеграл в последней строке совпадает с исходным интегралом. Перенесём его влево и разделим на 2 полученный результат:

.

Решить самостоятельно: [1] № 3770, 3772, 3774, 3775, 3777.