
- •1. Скалярное поле. Поверхности и линии уровня. Производная по направлению и градиент
- •Производная по направлению
- •Градиент скалярного поля
- •2. Поток векторного поля
- •1) Найти поток векторного поля через поверхность сферы
- •3. Криволинейные координаты. Теорема гаусса-остроградского. Дивергенция векторного поля
- •Теорема Гаусса - Остроградского
- •4. Линейный интеграл в векторном поле. Циркуляция векторного поля и ротор
- •Подставив всё это в интеграл, получим:
- •5. Теорема стокса. Независимость линейного интеграла от пути интегрирования. Потенциальное векторное поле
- •6. Оператор гамильтона “набла”. Дифференциальные операции первого и второго порядка
- •7. Заключение
- •Литература
1. Скалярное поле. Поверхности и линии уровня. Производная по направлению и градиент
Определение.Если в каждой точке области
![]() пространства определено значение
некоторой величины, то говорят, что
задано поле этой величины. Поле называется
скалярным, если величина вполне
характеризуется своим числовым значением.
пространства определено значение
некоторой величины, то говорят, что
задано поле этой величины. Поле называется
скалярным, если величина вполне
характеризуется своим числовым значением.
Скалярное
поле считается заданным, если в каждой
точке области
![]() определена скалярная функция
определена скалярная функция
![]() .
.
Геометрическое место точек, в которых скалярная функция принимает определённое значение, называется поверхностью уровня. Уравнение поверхности уровня имеет вид
![]()
![]() .
.
Примеры скалярных полейполе температуры, поле электрического потенциала.
Пример 1.1.Построить поверхности уровня скалярного поля
![]()
Решение.
![]()
Это однопараметрическое семейство параллельных плоскостей, гдеС параметр.
Пример
1.2Найти поверхности уровня
скалярного поля![]() ,
где
,
где
![]() постоянный
вектор,
постоянный
вектор,
![]() радиус-вектор
точки.
радиус-вектор
точки.
Решение.
Скалярное
произведение
![]()
уравнение
поверхности уровня
![]() откуда следует
откуда следует![]() или
или![]()
Это уравнение семейства параллельных плоскостей.
Найти самостоятельноповерхности уровня следующих скалярных полей:
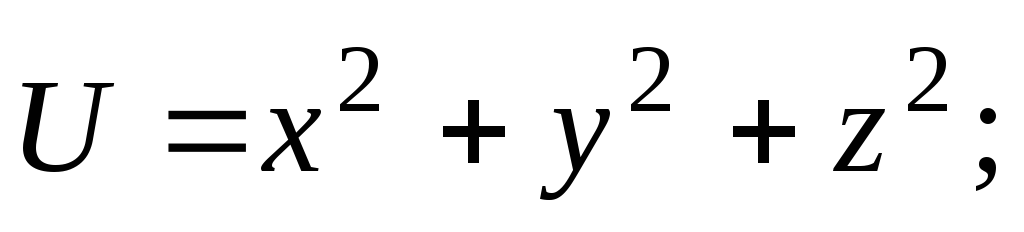

 (
(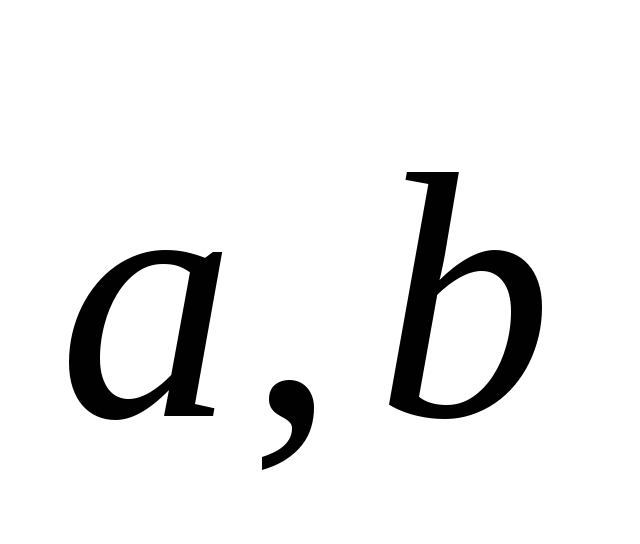 постоянные векторы.)
постоянные векторы.)
Если скалярное поле задано функцией двух переменных, например
![]() ,
,![]()
то его называют плоским. Поверхности уровня в этом случае вырождаются в линии уровня, определяемые уравнением
![]() .
.
Примером использования линий уровня для практических целей является физическая географическая карта, где с помощью линий уровня выявляется рельеф земной поверхности.
Пример 1.3.Найти линии уровня скалярного поля
![]()
Решение.
Линии уровня определяются уравнением
![]()
При
![]() получаем пару прямых
получаем пару прямых![]() и
и![]() при
при![]() семейство гипербол.
семейство гипербол.
Найти самостоятельнолинии уровня следующих плоских полей:
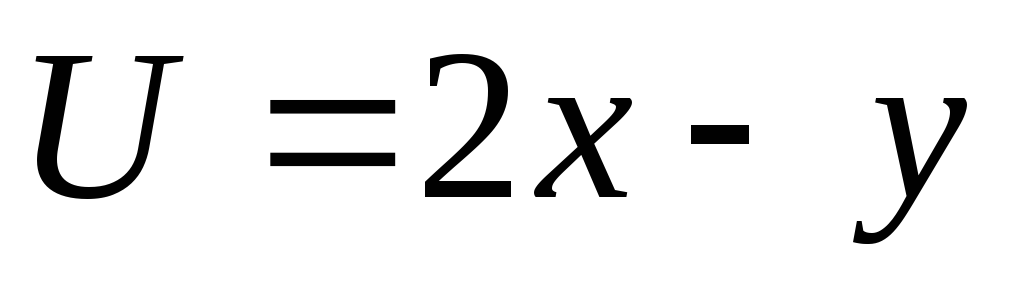 ;
; ;
;
Производная по направлению
Пусть
в некоторой области
![]() трёхмерного пространства задано
скалярное поле, определяемое функцией
трёхмерного пространства задано
скалярное поле, определяемое функцией
![]() .
.
Фиксируем
точку
![]() и выберем направление, определяемое
вектором
и выберем направление, определяемое
вектором![]() ,
орт которого
,
орт которого
![]() .
.
Обозначим
![]() .
Точку
.
Точку![]() выберем так, чтобы вектор
выберем так, чтобы вектор![]() совпадал
с
совпадал
с![]() .
.
![]()
откуда следует :
![]() ,
,
или
 (1.1)
(1.1)
Пусть
![]() ,
,![]() приращение вектора
приращение вектора![]()
Определение.Предел отношения
![]() ,
если он существует при
,
если он существует при![]() называется производной функции
называется производной функции![]() в точке
в точке![]() по направлению
по направлению
![]() и обозначается символом
и обозначается символом![]() ,
т.е.
,
т.е.
![]()
Согласно правилу дифференцирования сложной функции
![]()
Из соотношений (1.1) следует, что
![]()
![]()
![]()
Подставив последние соотношения в предыдущее выражение, получим:
![]() .
(1.2)
.
(1.2)
Здесь
символ
![]() и
аналогичные означают, что производные
вычисляются в точке
и
аналогичные означают, что производные
вычисляются в точке![]() .
.
Пример
1.4.Найти производную скалярного
поля![]() в точке
в точке
![]() по
направлению к точке
по
направлению к точке
![]() .
.
Решение.
Вектор
![]() модуль вектора
модуль вектора![]()
орт вектора
![]()
следовательно,
![]()
![]() ,
,
![]() .
.
Значения
частных производных функции
![]() в точке
в точке![]() равны:
равны:
![]()
![]()
![]()
Подставив всё в формулу (1.2), получим:
![]()
Решить самостоятельно
В
следующих задачах найти производные
функции
![]() по направлению от точки
по направлению от точки![]() к точке
к точке![]() :
:

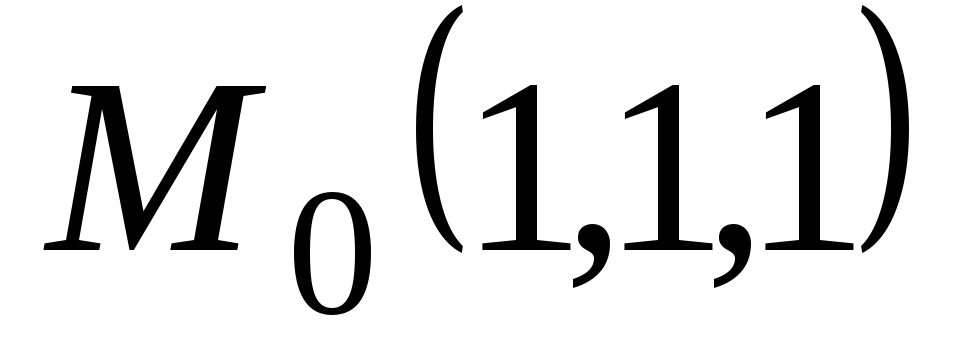 ,
,
 ;
;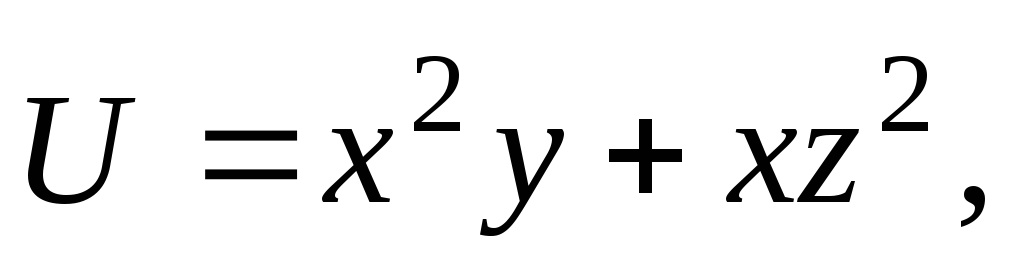
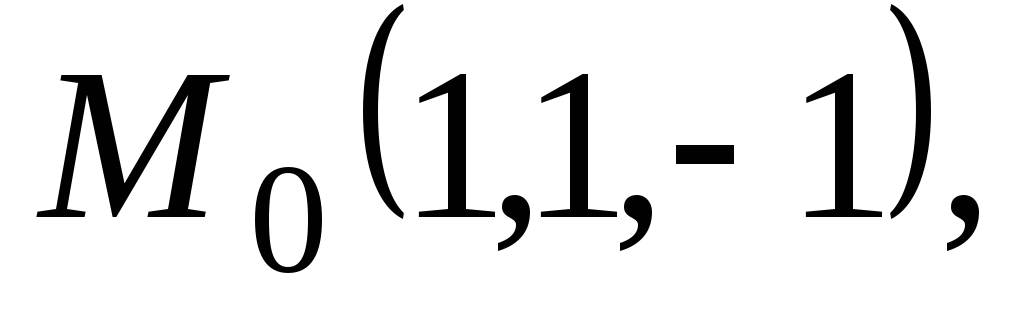
 ;
; в
точке
в
точке
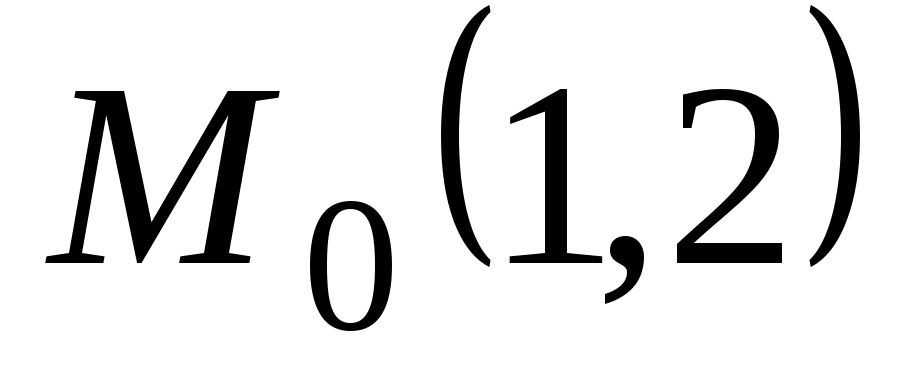 по направлению параболы
по направлению параболы ;
;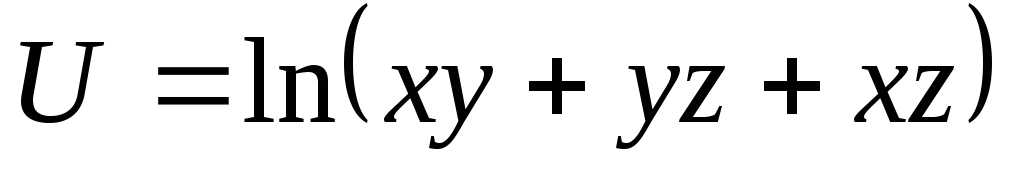 в
точке
в
точке
 по направлению окруж-ности
по направлению окруж-ности
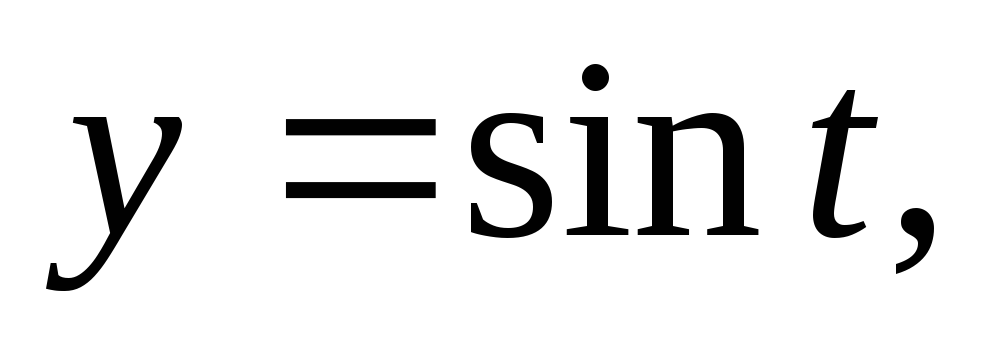

Градиент скалярного поля
Пусть
в области
![]() пространства функция
пространства функция![]() задаёт скалярное поле. Функция
задаёт скалярное поле. Функция![]() непрерывна и дифференцируема.Определение.Градиентом скалярного поля
непрерывна и дифференцируема.Определение.Градиентом скалярного поля
![]() в точке
в точке![]() называется вектор, обозначаемый
символом
называется вектор, обозначаемый
символом![]() и определяемый равенством
и определяемый равенством
![]() , (1.3)
, (1.3)
Сопоставив последнее выражение с формулой (1.2), получим
![]()
где
![]() орт
направления
орт
направления
![]()
Очевидно,
что производная функции
![]() по направлению вектора
по направлению вектора![]() есть
проекция вектора
есть
проекция вектора![]() на ось, направленную по
на ось, направленную по![]()
Градиент обладает следующими свойствами:
градиент направлен по нормали к поверхности уровня (или к линии уровня);
градиент направлен в сторону возрастания функции U;
модуль градиента равен наибольшему значению производной по направлению в данной точке поля;
![]()
Эти
свойства позволяют сделать вывод, что
![]() есть вектор, по величине и направлению
характеризующий наибольшую крутизну
изменения функции
есть вектор, по величине и направлению
характеризующий наибольшую крутизну
изменения функции![]() .
.
Пример
1.5.Найти градиент скалярного поля![]() .
.
Решение.
![]()
![]() нормальный
вектор для семейства параллельных
плоскостей
нормальный
вектор для семейства параллельных
плоскостей
![]() ,
,
которые являются поверхностями уровня данного скалярного поля.
Пример 1.6
Найти
наибольшую крутизну подъёма поверхности
![]() в точке
в точке![]() .
.
Решение.
![]()
![]()
![]()
Пример 1.7.
Найти направление наибольшего изменения скалярного поля
![]()
и
величину этого изменения в точке
![]()
Решение.
Направление
наибольшей крутизны изменения поля
задаёт вектор
![]() .
.
![]() .
.
![]()
Решить самостоятельно:
найти градиент скалярного поля
![]() в
точке
в
точке
![]() ;
;
найти угол
 между градиентами функции
между градиентами функции
![]() в
точках
в
точках
![]() и
и![]() ;
;
найти угол
 между градиентами функций
между градиентами функций
![]() и
и
![]() в точке
в точке![]() ;
;
14)
найти градиент
![]() ,
если
,
если
![]()
![]()
![]() постоянный
вектор.
постоянный
вектор.
Ответы.
 семейство
сферических поверхностей;
семейство
сферических поверхностей; семейство
параболоидов;
семейство
параболоидов; пучок
плоскостей;
пучок
плоскостей;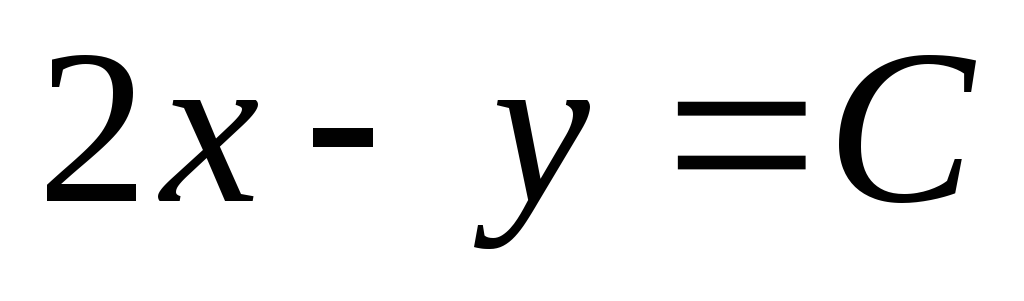 семейство
параллельных прямых;
семейство
параллельных прямых; пучок
прямых;
пучок
прямых; семейство
парабол;
семейство
парабол; 8)
8)
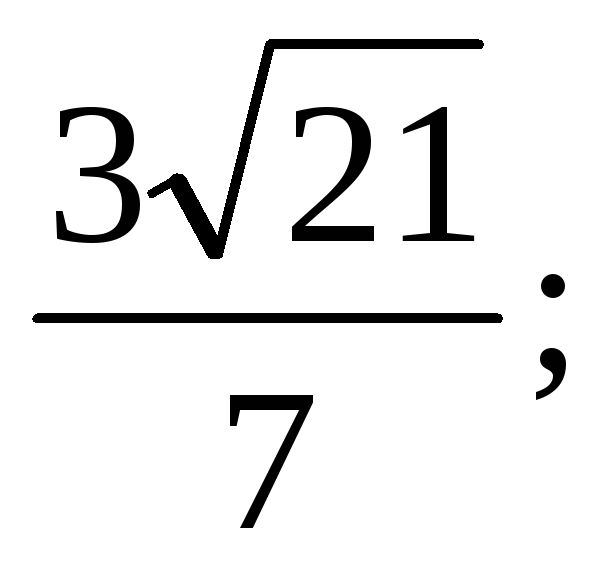 9)
9) 10) -2 ; 11)
10) -2 ; 11) ;
;
12)
![]() 13)
13)![]() 14)
14)![]()
