ОГЛАВЛЕНИЕ

1. ДВОЙНЫЕ ИНТЕГРАЛЫ…………………………………………………………4

1.1. Задача об объёме цилиндрического бруса…………………………...4

1.2. Условия существования двойного интеграла………………………..5

1.3. Свойства двойных интегралов………………………………………..7

2. ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ……………………………………9

3. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ…..…………………22

4. ТРОЙНОЙ ИНТЕГРАЛ………………………………………………………...…35

4.1. Определение и условия существования тройного интеграла ……..35

4.2. Вычисление тройного интеграла в декартовых координатах……..36

5. ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА В КРИВОЛИНЕЙНЫХ СИСТЕ-МАХ КООРДИНАТ…………………………………………………………..………...44

5.1. Замена переменных в тройном интеграле…………………………..44

5.2. Поверхности второго порядка……………………………………….47

5.3. Примеры………………………………………………………………54

6. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА…………………………..61

7. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА……………………….....68

ЛИТЕРАТУРА…………………………………………………………….76

1. Двойные интегралы

1. Задача об объёме цилиндрического бруса

Подобно тому, как задача о площади криволинейной трапеции привела нас во втором семестре к понятию определенного интеграла от функции одной переменной , аналогичная задача об объёме цилиндрического бруса приведёт к новому понятию – двойного определённого интеграла от функции двух переменных.

Рассмотрим тело, ограниченное сверху поверхностью , снизу – фигурой, лежащей в плоскости, а с боков – цилиндрической поверхностью с образующими, параллельными оси, направляющей для которых служит кривая, ограничивающая область.

Для решения задачи используем обычный в интегральном исчислении приём, который сводится к разложению искомой величины на элементарные части, приближенному подсчёту каждой части, суммированию и последующему предельному переходу.

С этой целью разделим область сетью кривых на частии рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями эти частичные области и в сумме составляют данное тело.

Для подсчёта объёмов этих столбиков фиксируем произвольно в каждой частичной области по точке с координатами- кси,- эта греческие буквы). Высоту каждого столбика будем считать равной . Тогда объём каждого столбика

,

где  площадь основания элементарного цилиндра.

В этом случае приближенное выражение для объёма тела

. (1.1)

Для повышения точности этого равенства будем уменьшать размеры площадок , увеличивая их число. В пределе, при стремлении к нулю наибольшего из диаметров областей, это равенство становится точным:

, (1.2)

Предел (1.2) и есть двойной интеграл от функции по области, и формула для объёма принимает вид:

. (1.3)

2. Условия существования двойного интеграла

Для квадрируемости области, ограниченной какой-либо кривой, необходимо и достаточно, чтобы эта кривая имела нулевую площадь. Такими кривыми являются гладкие кривые (имеющие непрерывные производные) или состоящие из конечного числа гладких кусков (так называемые кусочно-гладкие).

Будем предполагать, что как контур области , так и кривые, которыми мы разбиваем её на части, имеют площадь, равную нулю. Этим обеспечивается существование всех нужных нам площадей.

Определенную ранее сумму (1.1) будем называть интегральной суммой и обозначать греческой буквой (- сигма):

.

Сформулируем определение двойного интеграла Римана.

Определение. Конечный предел интегральной суммы при, если он существует для любого разбиения областина частии не зависит от выбора точек, принадлежащих, называется двойным интегралом от функциив областии обозначается символом

.

Функция, имеющая интеграл, называется интегрируемой. Интегрируемая функция должна быть ограниченной. Действительно, в противном случае можно было бы за счёт выбора точек сделать интегральную сумму произвольно большой. Поэтому будем полагать, что существуют такие числаи, что

.

Для уяснения условий существования двойного интеграла введем в рассмотрение так называемые нижнюю и верхнюю суммы Дарбу:

, (1.4)

где и соответственно точные нижняя и верхняя грани функциив области.

При данном разбиении области на части, независимо от выбора точек, будут выполняться неравенства

.

За счёт выбора этих точек можно значения сделать сколь угодно близкими кили к, а вместе с этим суммусделать сколь угодно близкой кили к. Следовательно, нижняя и верхняя суммы Дарбу являются, соответственно, точными нижней и верхней гранями интегральных сумм, отвечающих одному разбиению области.

Суммы Дарбу обладают следующими свойствами:

1. При дроблении частей с добавлением к старым линиям деления новых нижняя сумма Дарбу не убывает, а верхняя не возрастает.

2. Каждая нижняя сумма Дарбу не превосходит каждой верхней суммы, хотя бы и отвечающей другому разбиению области .

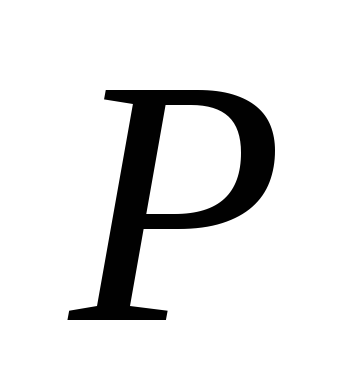Сформулируем теорему существования двойного интеграла.

Теорема. Для существования двойного интеграла необходимо и достаточно условие

,

или в других обозначениях

(1.5)

где есть колебание функциив частичной области(- омега).

Теорема существования интеграла позволяет установить классы интегрируемых функций:

I. Всякая непрерывная в области функцияинтегрируема.

II. Ограниченная функция , имеющая разрывы лишь на конечном числе линий с нулевой площадью, интегрируема.