5. Вычисление тройного интеграла в криволинейных системах координат

5.1. Замена переменных в тройном интеграле

Если ограниченная замкнутая область пространствавзаимно однозначно отображается в областьпространствас помощью непрерывно дифференцируемых функций

и якобиан преобразования не обращается в нуль, то справедлива формула

, (5.1)

где

.

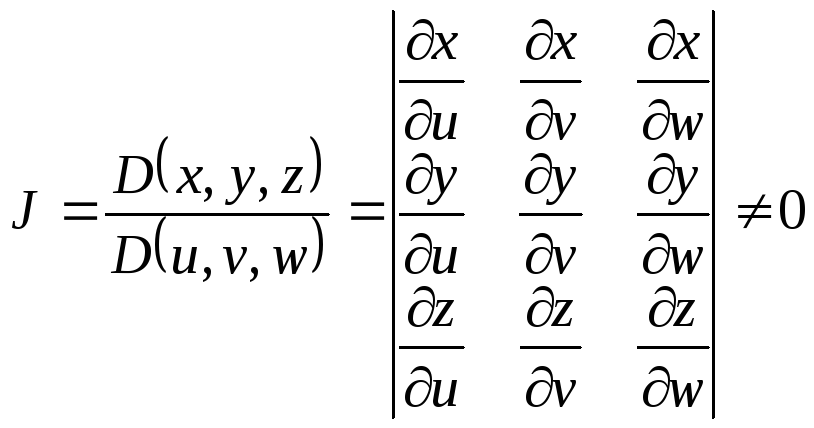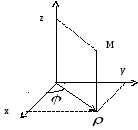
Рис. 5.1

В частности, при переходе к цилиндрическим координатам:

(рис. 5.1), связанным с формулами

,

,

формула (5.1) принимает вид:

. (5.2)

Здесь якобиан перехода к цилиндрическим координатам

.

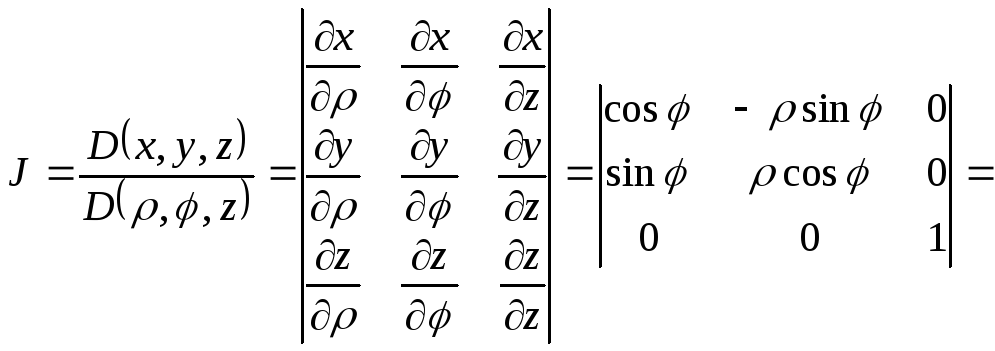
Интегрирование в примере 4.3 предыдущего раздела можно провести иначе, заменив тройной интеграл тремя последовательно вычисляемыми интегралами, имея в виду, что радиус окружности, по которой пересекаются две сферы,

.

Целесообразно в этом случае перейти к цилиндрическим координатам. Тогда уравнения поверхностей, ограничивающих тело снизу и сверху, будут иметь вид:

.

Расставив пределы в повторных интегралах, получим

.

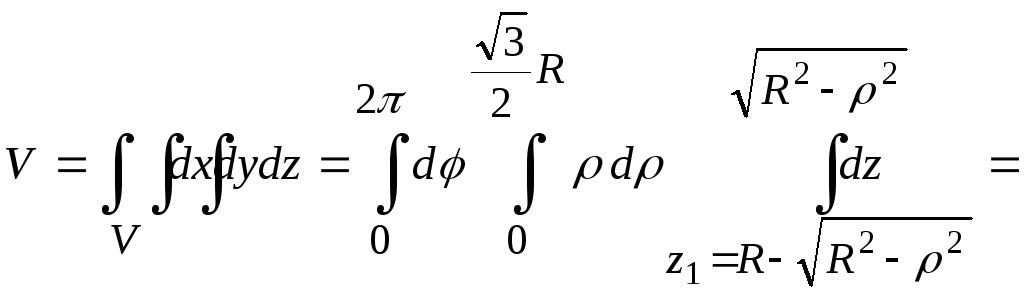
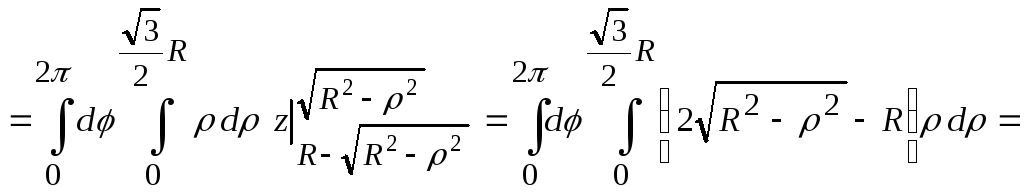
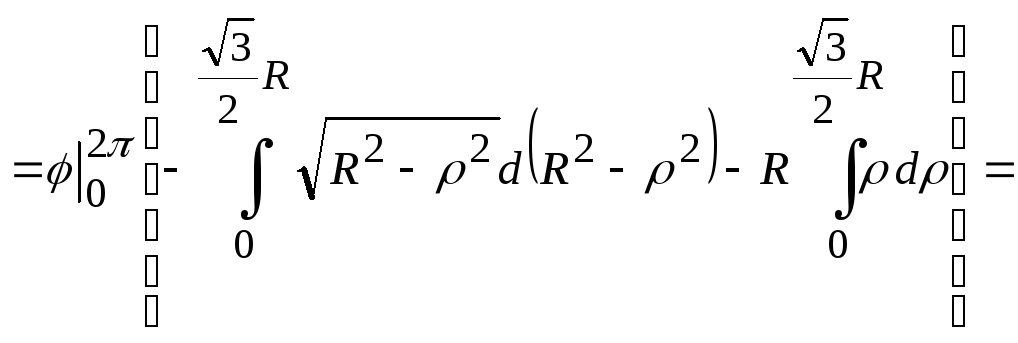
При переходе к сферическим координатам связь с декартовыми координатамиустанавливается соотношениями:

(рис.5.2).

Вычислим якобиан преобразования:

.

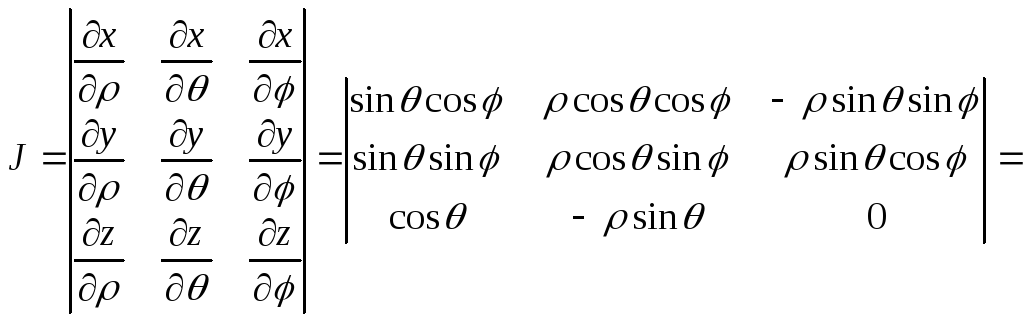
Формула (5.1) в сферических координатах принимает вид

. (5.4)

Сферические координаты – это координаты на поверхности сферы, в частности земной сферы, где  расстояние до центра сферы,  долгота, а  широта, причём, на северном полюсе,на экваторе ина южном полюсе.

Рис. 5.2

5.2. Поверхности второго порядка

При вычислении тройных интегралов расстановка пределов в повторных интегралах затруднительна без построения пространственных областей, в которых проводится интегрирование. Границами рассматриваемых областей оказываются, как правило, поверхности второго порядка. Поэтому целесообразно повторить соответствующий раздел аналитической геометрии.

Сфера, центр которой находится в начале координат, в декартовой системе координат имеет уравнение

.

Уравнение сферы в цилиндрических координатах получим, подставив в это уравнение соотношения

.

Разрешив последнее уравнение относительно , будем иметь

.

Здесь положительная ветвь решения уравнения описывает верхнюю полусферу, а отрицательная  нижнюю.

Уравнение сферы в сферических координатах получается в результате подстановки в уравнение соотношений

;

. Уравнение сферы с центром, смещенным по одной из осей 

.

Это  сфера, смещенная в положительную сторону по оси на радиус.

В цилиндрических координатах её уравнение преобразуется к виду

или

.

Здесь ветвь решения со знаком плюс перед корнем описывает верхнюю полусферу, а со знаком минус  нижнюю.

В сферических координатах уравнение смещенной сферы приводится к виду

.

Рассмотрим другие поверхности второго порядка.

Изменив знак перед квадратом одной из переменных в каноническом уравнении сферы, получим уравнение однополостного гиперболоида:

.

Выявить форму полученной поверхности можно, рассекая её координатными плоскостями или плоскостями, параллельными коорди-натным.

Рассечем поверхность плоскостью , уравнение которой.

Решение системы уравнений

есть уравнение гиперболы

,

принадлежащей плоскости и пересекающей осьв точках.

В сечениях поверхности горизонтальными плоскостями иполучим окружности:

и .

Этой информации достаточно для изображения эскиза однополостного гиперболоида (рис. 5.3).

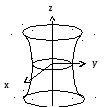
Рис. 5.3

В цилиндрических координатах уравнение однополостного гиперболоида имеет вид

.

Двуполостной гиперболоид получается, если в каноническом уравнении сферы поменять знаки перед и:

.

В сечении поверхности плоскостью () получим гиперболу, решив систему уравнений:

Полученная гипербола описывается уравнением

.

Точки пересечения гиперболы с осью имеют координаты.

В сечениях поверхности горизонтальными плоскостями

()

получаются окружности, описываемые уравнением

.

Эскиз поверхности изображен на рис. 5.4.

Уравнение двуполостного гиперболоида в цилиндрических координатах имеет вид

или .

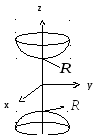
Рис. 5.4

Изменив в каноническом уравнении сферы знак при и приравняв нулю радиус (), получим уравнение конической поверхности:

В сечении конуса плоскостью получаются две прямые:

и ,

а в сечениях горизонтальными плоскостями  окружности:

.

Уравнение конической поверхности в цилиндрических координатах имеет вид

или .

Уравнение конуса в сферических координатах

.

Эскиз конической поверхности приведен на рис. 5.5.

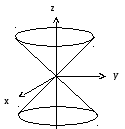
Рис. 5.5

Рассмотрим параболоиды.

Каноническое уравнение параболоида вращения 

.

Эскиз параболоида вращения показан на рис. 5.6.

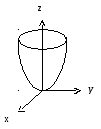
Рис. 5.6

В сечении поверхности плоскостью получается парабола

,

а в сечении плоскостью  окружность

.

Уравнение параболоида вращения в цилиндрических координатах 

.

Гиперболический параболоид имеет уравнение

или .

Эскиз поверхности изображен на рис. 5.7.

Рис. 5.7

В сечениях гиперболического параболоида вертикальными коорди-натными плоскостями иполучаются параболы:

и .

В сечениях горизонтальными плоскостями  гиперболы

.

При гиперболы вырождаются в прямые

и .

Поверхности второго порядка можно деформировать, сжимая или растягивая в направлении координатных осей. В уравнениях поверхностей в этом случае появятся коэффициенты деформации. В результате такой деформации из сферы получается эллипсоид, имеющий уравнение

,

а также одополостной и двуполостной гиперболоиды и конические поверхности. Уравнения этих поверхностей, соответственно 

.

С помощью круговой перестановки переменных в этих уравнениях могут быть получены уравнения названных поверхностей, симметричных относительно других осей координат.

Аналогичным деформациям можно подвергнуть и уравнения параболоидов. В итоге будут получены уравнения:



уравнение эллиптического параболоида и



уравнение гиперболического параболоида.

Утверждения относительно круговой перестановки переменных справедливы и для уравнений параболоидов.

Цилиндрические поверхности

Цилиндрической поверхностью называется поверхность, образованная в результате перемещения некоторой прямой, называемой образующей цилиндра, вдоль некоторой кривой, именуемой направляющей. При этом образующая в процессе перемещения остается параллельной своему исходному положению.

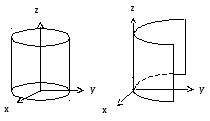
Рис. 5.8

Если образующая параллельна одной из осей координат, то переменная, соответствующая этой оси, в уравнении цилиндра будет отсутствовать. Это значит, что никаких ограничений на данную переменную не наложено и она может принимать любые действительные значения.

Уравнение направляющей кривой в этом случае задается, как правило, в координатной плоскости, перпендикулярной к образующей, и к этому уравнению сводится уравнение цилиндра.

Пусть, например, образующая цилиндра параллельна оси . Тогда уравнение

есть уравнение эллиптического цилиндра, а уравнение

есть уравнение параболического цилиндра.

Эскизы этих поверхностей приведены на рис. 5.8.

В рассматриваемых далее примерах полученную информацию о поверхностях второго порядка следует использовать при расстановке пределов интегрирования.