
- •1. Двойные интегралы
- •Задача об объёме цилиндрического бруса
- •Условия существования двойного интеграла
- •1.3. Свойства двойных интегралов
- •Вычисление двойных интегралов
- •3. Замена переменных в двойном интеграле
- •4. Тройной интеграл
- •4.1. Определение и условия существования тройного интеграла
- •4.2. Вычисление тройного интеграла в декартовых координатах
- •5. Вычисление тройного интеграла в криволинейных системах координат
- •5.1. Замена переменных в тройном интеграле
- •5.2. Поверхности второго порядка
- •5.3. Примеры
- •Объём тела удобно вычислять тройным интегралом:
- •6. Криволинейный интеграл первого рода
- •7. Поверхностный интеграл первого рода
- •Литература
3. Замена переменных в двойном интеграле
Пусть
заданы две прямоугольные системы
координат
![]() и
и![]() .
.
Рассмотрим
две плоские области: область
![]() на плоскости
на плоскости![]() и область
и область![]() на плоскости
на плоскости![]() (рис. 3.1). Допустим, что в области
(рис. 3.1). Допустим, что в области![]() определена система непрерывных и
однозначных функций
определена система непрерывных и
однозначных функций
![]() (3.1)
(3.1)
которая
каждую точку
![]() области
области![]() отображает в единственную точку
отображает в единственную точку![]() области
области![]() .
.
Пусть
функции системы (3.1) разрешимы относительно
переменных
![]() и
и![]() и полученные функции однозначны и
непрерывны:
и полученные функции однозначны и
непрерывны:
![]() (3.1а)
(3.1а)
Система
(3.1а) отображает каждую точку
![]() области
области![]() в единственную точку
в единственную точку![]() области
области![]() .
.
Считают
в этом случае, что формулы (3.1) и (3.1а)
устанавливают взаимно однозначное
соответствие между точками областей
![]() и
и![]() .
.

Рис. 3.1
Элементарная
площадка на плоскости
![]()
![]() отображается в элементарную площадку
отображается в элементарную площадку![]() на плоскости
на плоскости![]() и при этом как-то искажается (растягивается
или сжимается).
и при этом как-то искажается (растягивается
или сжимается).
Рассмотрим геометрический вывод для коэффициента искажения элемента площади при преобразовании координат, предложенный М.В. Остроградским. Этот вывод обладает очевидным преимуществом наглядности, хотя и не вполне строг.
Выделим
на плоскости
![]() бесконечно малый прямоугольник
бесконечно малый прямоугольник![]() со сторонами
со сторонами![]() и
и![]() ,
параллельными координатным осям. На
плоскость
,
параллельными координатным осям. На
плоскость![]() он отобразится в криволинейный
четырёхугольник
он отобразится в криволинейный
четырёхугольник![]() (рис. 3.1).
(рис. 3.1).
Определим
его площадь. Вершины прямоугольника на
плоскости
![]() имеют
координаты:
имеют
координаты:
![]() .
.
Соответствующие
вершины четырёхугольника
![]() на
плоскости
на
плоскости![]() будут иметь следующие координаты:
будут иметь следующие координаты:
![]()
![]()
![]()
![]()
![]()
Если
ограничиться членами первого порядка
относительно
![]() и
и![]() ,
координаты точек можно представить
так:
,
координаты точек можно представить
так:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Все
производные здесь вычислены в точке
![]() .
Поскольку проекции отрезков
.
Поскольку проекции отрезков![]() и
и![]() на обе оси соответственно равны,
четырёхугольник
на обе оси соответственно равны,
четырёхугольник![]() есть параллелограмм (с точностью до
малых высшего порядка).
есть параллелограмм (с точностью до
малых высшего порядка).
Площадь
параллелограмма равна модулю векторного
произведения векторов
![]() и
и![]() .
Векторы в компонентах можно записать
так:
.
Векторы в компонентах можно записать
так:
![]() ,
,
![]() ,
,
и вычислить модуль их векторного произведения:
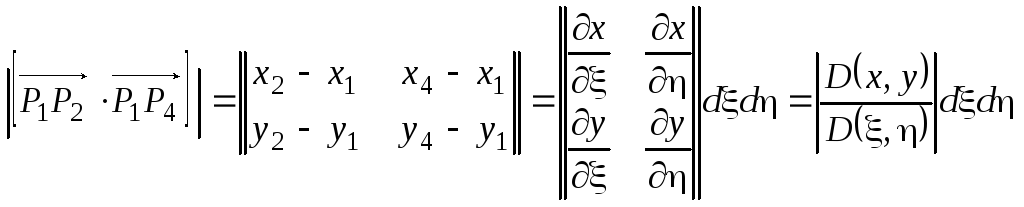 .
.
Определитель, элементами которого являются частные производные, называется определителем Якоби, или якобианом. В правой части равенства представлена его компактная запись.
Для якобианов известно следующее соотношение:
![]() , (3.2)
, (3.2)
или в подробной записи:
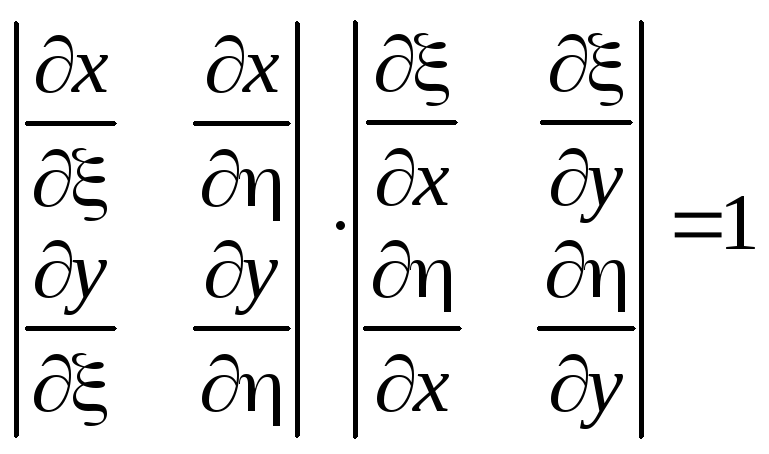 .
.
Двойной интеграл при замене переменных
![]()
преобразуется следующим образом:
![]() . (3.3)
. (3.3)
Наиболее
важным и часто используемым примером
криволинейных координат являются
полярные координаты
![]() ,
где
,
где![]()
радиус-вектор точки,
радиус-вектор точки,
![]()
полярный угол, отсчитываемый от
направления полярной оси, совпадающей
с осью
полярный угол, отсчитываемый от
направления полярной оси, совпадающей
с осью
![]() ,
в направлении против часовой стрелки.
,
в направлении против часовой стрелки.
Декартовы и полярные координаты связаны соотношениями
![]() .
.
Взаимно
однозначное соответствие между
декартовыми и полярными координатами
имеет место лишь при выполнении
ограничений, наложенных на величины
![]() и
и![]() .
.
Якобиан в этом случае
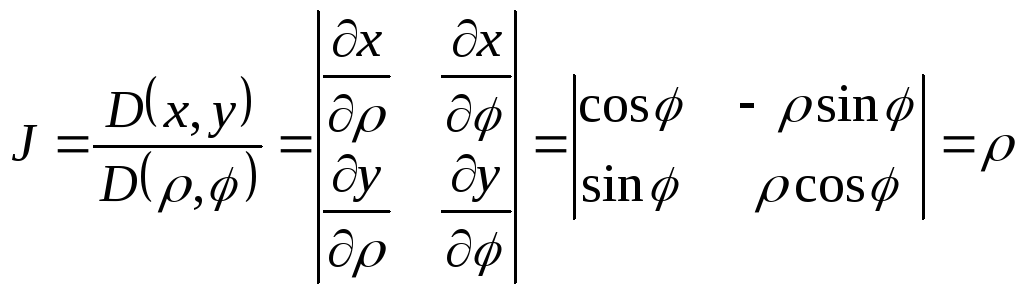 ,
,
а двойной интеграл преобразуется так:
![]() . (3.4)
. (3.4)
Пример
3.1. При какой
замене переменных криволинейный
четырёхугольник
![]() ,
ограниченный линиями
,
ограниченный линиями
![]() ,
,
превратится
в прямоугольник, стороны которого
параллельны осям координат
![]() и
и![]() (рис. 3.2)?
(рис. 3.2)?
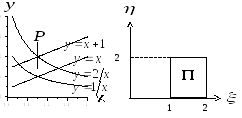

Рис. 3.2
Решение.
Замена переменных
![]() решает задачу. Границы искомого
прямоугольника
решает задачу. Границы искомого
прямоугольника![]() будут иметь уравнения:
будут иметь уравнения:
![]()
Пример 3.2 Вычислить двойной интеграл:
![]() ,
,
где
![]()
параллелограмм, ограниченный прямыми
линиями:
параллелограмм, ограниченный прямыми
линиями:
![]() ,
(рис. 3.3).
,
(рис. 3.3).
Произведем замену переменных:
![]() (3.5)
(3.5)
Область
интегрирования
![]() отобразится в прямоугольник
отобразится в прямоугольник![]() ,
границы которого имеют уравнения:
,
границы которого имеют уравнения:
![]() .
.
Из
системы (3.5)
легко получить соотношения
![]() и вычислить якобиан преобразования
координат:
и вычислить якобиан преобразования
координат:
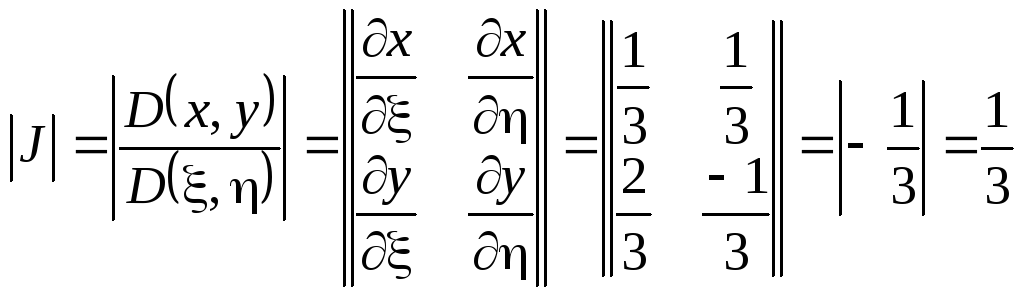 .
.
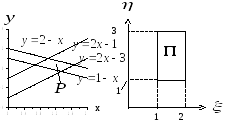
Рис. 3.3
Вычислим интеграл:
![]() .
.
Пример 3.3. Вычислить интеграл:
![]()
по
области
![]() ,
заключенной между параболами
,
заключенной между параболами![]() и гиперболами
и гиперболами![]() (рис. 3.4).
(рис. 3.4).
Решение. Произведём замену переменных:
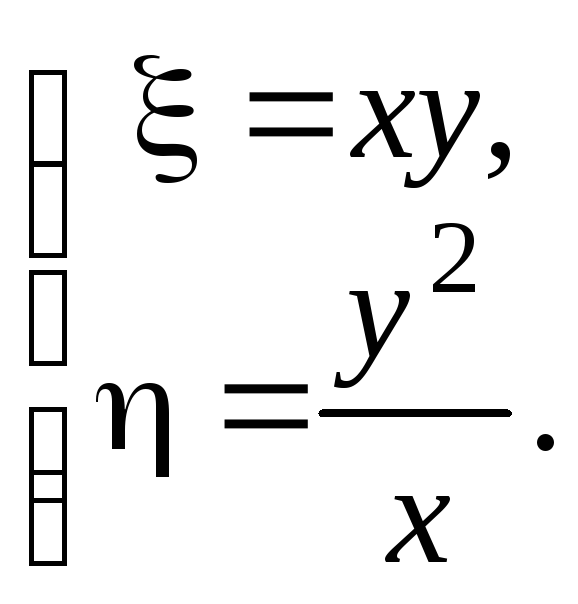
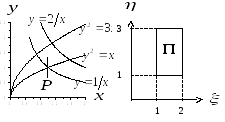
Рис. 3.4
Область
![]() будет отображена в область
будет отображена в область![]() ,
ограниченную прямыми
,
ограниченную прямыми
![]()
При вычислении якобиана учтём соотношение (3.2):
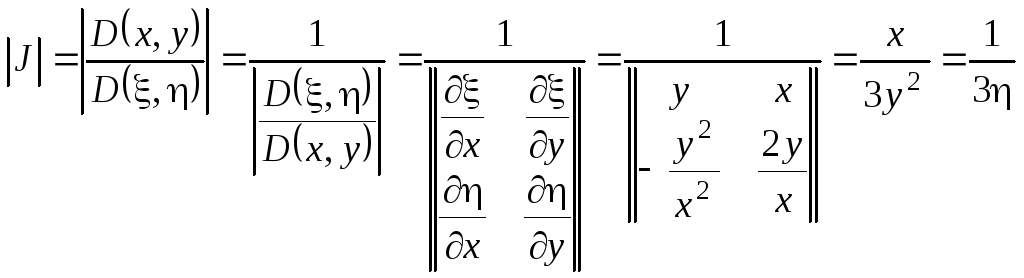 .
.
Вычислим интеграл:
![]() .
.
Пример 3.4. Вычислить двойной интеграл:
![]() .
.
Область
![]() представляет собой часть круга
представляет собой часть круга![]() ,
не принадлежащую кругу
,
не принадлежащую кругу![]() (рис.3.5).
(Первый из кругов смещён вправо по оси
(рис.3.5).
(Первый из кругов смещён вправо по оси![]() на радиус, центр второго – в начале
координат. Интеграл определяет площадь
области
на радиус, центр второго – в начале
координат. Интеграл определяет площадь
области![]() .)
.)
Решение. Перейдём к полярным координатам:
![]()
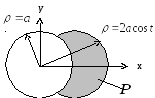
Рис. 3.5
Уравнения
границ области
![]() в полярных координатах преобразуются
следующим образом.
в полярных координатах преобразуются
следующим образом.
Первое уравнение:
![]()
![]() .
.
Второе уравнение:
![]() .
.
В соответствии с формулой (3.4) интеграл принимает вид
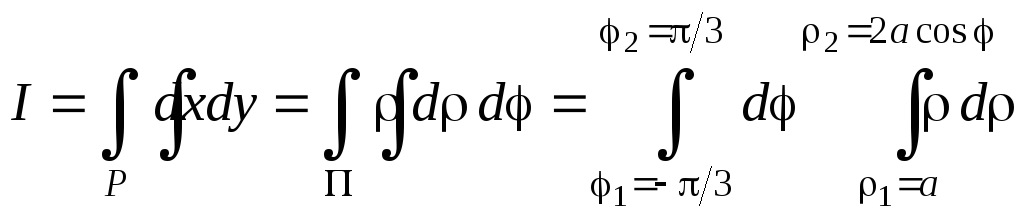 .
.
Вычислим внутренний интеграл:
![]() .
.
Полученный результат подставим во внешний интеграл и продолжим вычисления:
![]()
![]() .
.
(Переход к интегралу по половине симметричного промежутка интегри-рования возможен потому, что подынтегральная функция чётная. Результат интегрирования при этом, естественно, удваивается.)
Пример 3.5. Вычислить интеграл:
![]() .
.
Область
![]() ограничена лемнискатой (рис. 3.6)
ограничена лемнискатой (рис. 3.6)
![]() .
.
Решение. Перейдём к полярным координатам:
![]()
Подставим эти соотношения в уравнение лемнискаты и в подынтегральное выражение:
![]()
![]() .
.
![]() .
.
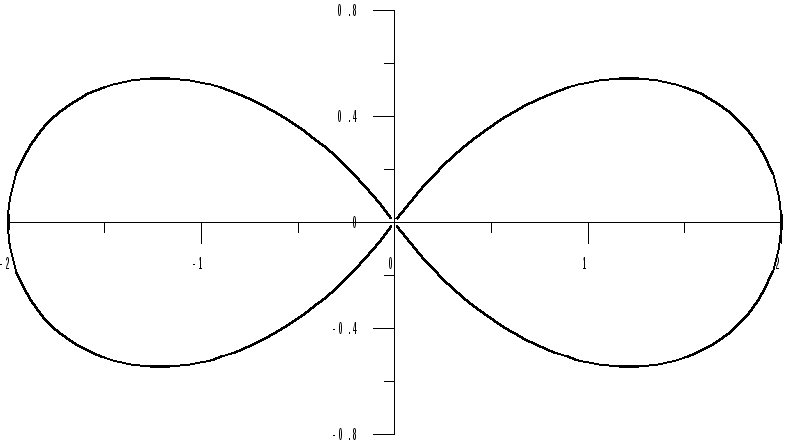
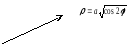
Рис. 3.6
Две
петли лемнискаты существуют при
![]()
правая, и при
правая, и при
![]()
левая. В промежутках
левая. В промежутках
![]() и
и![]() кривая не существует.
кривая не существует.
Интеграл в полярных координатах принимает вид
![]() .
.
Появление
коэффициента 4 перед повторным интегралом
объясняется тем, что интеграл вычисляется
по четверти области
![]() .
.
Вычислим внутренний интеграл:
![]()
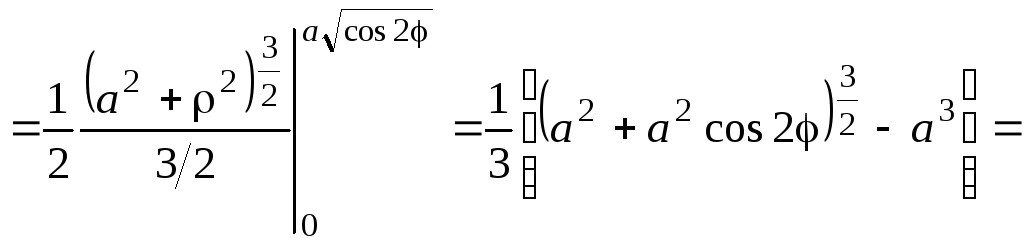
![]() .
.
Подставим полученное выражение во внешний интеграл и вычислим его:
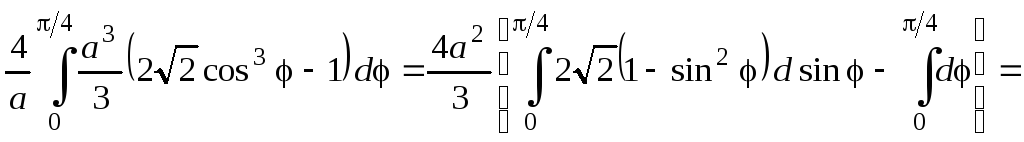
![]()
![]()
![]() .
.
Пример
3.6. Вычислить
двойной интеграл
![]()
по
области
![]() ,
ограниченной эллипсом
,
ограниченной эллипсом![]() .
.
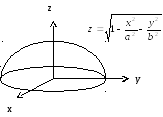
Рис. 3.7
Этот интеграл определяет объём половины эллипсоида:
![]() ,
,
расположенной
выше плоскости
![]() при
при![]() (рис. 3.7).
(рис. 3.7).
Решение. Введём обобщённые полярные координаты:
![]()
Найдём якобиан преобразования:
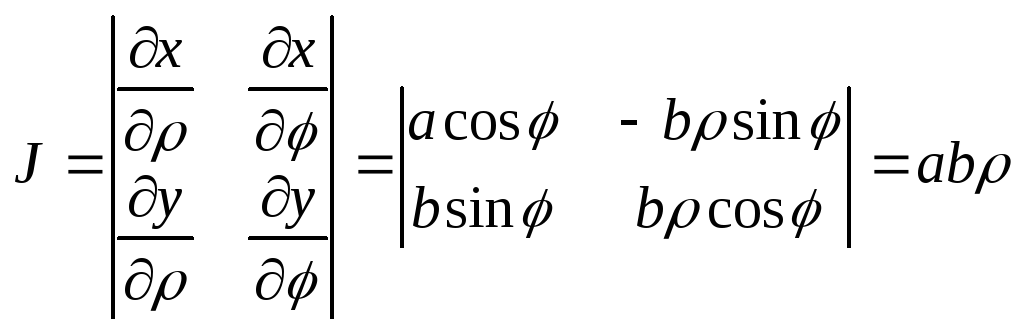 .
.
Преобразуем
подынтегральное выражение и уравнение
границы области
![]() :
:
![]() ,
,
![]() .
.
Область
![]() в результате замены переменных
преобразовалась в круг единичного
радиуса. Вычислим интеграл:
в результате замены переменных
преобразовалась в круг единичного
радиуса. Вычислим интеграл:
![]()
![]() .
.
Пример 3.7. Вычислить объём тела, ограниченного параболоидом
![]() и
плоскостью
и
плоскостью
![]() (рис. 3.8).
(рис. 3.8).
Решение. Линия пересечения параболоида и плоскости – окружность:
![]() .
.
Объём тела вычисляется с помощью интеграла:
![]() ,
,
где
область
![]() ограничена окружностью
ограничена окружностью![]() .
.
Перейдём к полярным координатам и вычислим интеграл:
![]()
 .
.
Рис. 3.8
Пример 3.8. Найти объём тела, ограниченного поверхностями:
![]()
Решение.
Тело
представляет собой цилиндр с вертикальными
образующими, снизу ограниченный
плоскостью
![]() ,
а сверху – параболоидом, уравнение
которого записано первым. Основание
цилиндра – круг радиусом
,
а сверху – параболоидом, уравнение
которого записано первым. Основание
цилиндра – круг радиусом![]() с центром, смещённым вправо по оси
с центром, смещённым вправо по оси![]() на радиус (уравнение второе). В большем
круге вырезано круглое отверстие
радиусом
на радиус (уравнение второе). В большем
круге вырезано круглое отверстие
радиусом![]() ,
тоже смещённое вправо по оси
,
тоже смещённое вправо по оси![]() на радиус (уравнение третье). Тело
симметрично относительно плоскости
на радиус (уравнение третье). Тело
симметрично относительно плоскости![]() ,
поэтому вычисляем объём половины тела
и удваиваем результат. Вычисления
произведём в полярных координатах:
,
поэтому вычисляем объём половины тела
и удваиваем результат. Вычисления
произведём в полярных координатах:
![]() .
.
Преобразуем уравнения:
![]() ,
,
![]() .
.
Вычислим объём тела:
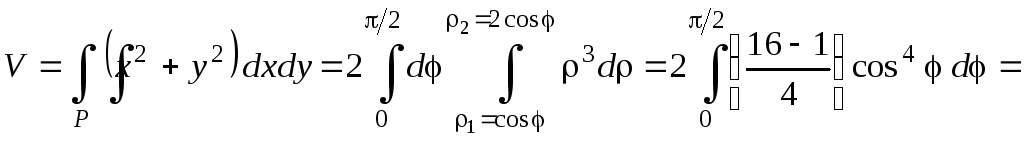
![]()
![]() ,
,
поскольку интегралы от косинусов обращаются в нуль. Например:
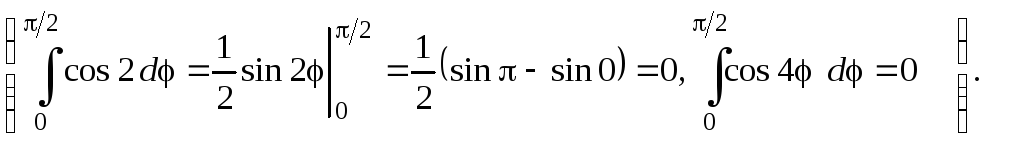
Пример 3.9 Вычислить объём тела, образованного пересечением параболоида
![]() и
плоскости
и
плоскости
![]() .
.
Решение.
Тело ограничено снизу параболоидом,
сверху плоскостью. Объём его можно
рассматривать как разность объёмов
вертикальных цилиндров с общим основанием
![]() на плоскости
на плоскости![]() .
Основание ограничено линией, являющейся
проекцией на плоскость
.
Основание ограничено линией, являющейся
проекцией на плоскость![]() линии пересечения параболоида и
плоскости. Чтобы получить уравнение
границы области
линии пересечения параболоида и
плоскости. Чтобы получить уравнение
границы области![]() ,
исключим
,
исключим![]() из уравнений параболоида и плоскости:
из уравнений параболоида и плоскости:
![]()
![]() .
.
Это
окружность радиусом
![]() с центром в точке
с центром в точке![]() .
.
Вычислим объём тела:
![]()
![]() .
.
Перенесём начало координат в центр окружности и перейдём к полярным координатам:
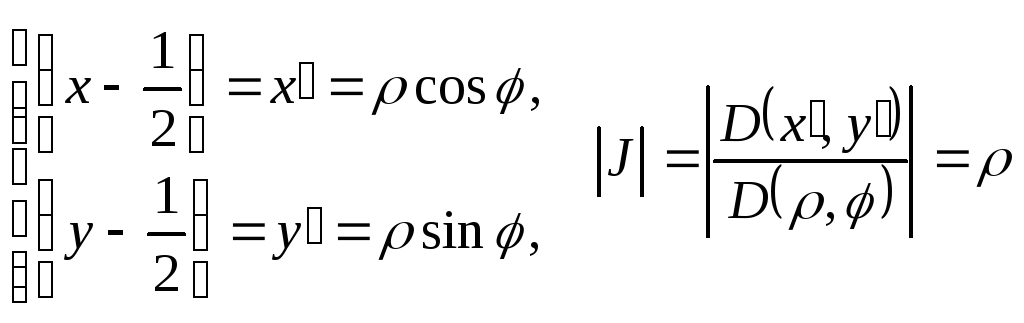 .
.
Тогда
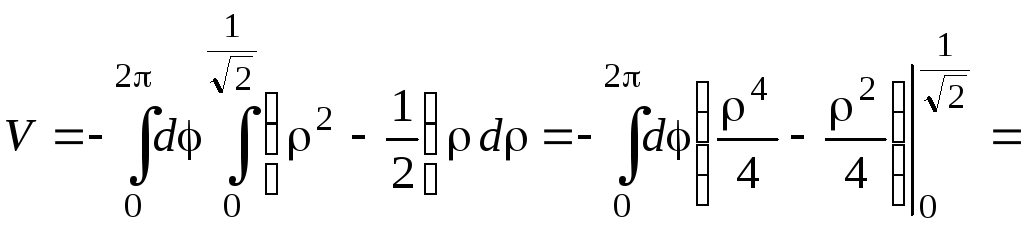
![]() .
.
Решить самостоятельно: [1] № 3564, 3565, 3567, 3568, 3575, 3577, 3587, 3588.
