
2012_Topology / met-srsTopology-2012
.pdfТопология |
21 |
расположенную на поверхности земного шара на 10 км южнее, чем ln. Тогда очевидно, что A = g1 g2 · · · g0, где g0 — одноточечное множество — южный полюс. Множество A не замкнуто. Для этого множества предельными точками являются все точки окружности l0 отстоящей на 10 км южнее северного полюса, эта окружность не входит в множество A.
Задача 3.
На R2 введена топология конечных дополнений. В получившемся топологическом пространстве X найти внутренность, границу и внешние точки для а) круга x2 + y2 < 1; б) точки {0}.
Решение задачи 3.
а) Окрестность каждой точки круга — это R2, из которого выколото конечное число точек. Такой же вид имеют и окрестности любой точки дополнения круга. Очевидно,всякая такая окрестность пересекается как с кругом, так и с его дополнением, и значит любая точка X является граничной для круга. Внешних и внутренних точек нет.
б) Границей точки {0} является она сама, поскольку любая содержащая ее окрестность содержит и точки, отличные от {0}. Остальные точки X являются внутренними, поскольку лежат в дополнении R2 \{0} вместе со своей окрестностью (в качестве которой можно выбрать само дополнение R2 \ {0}). Внешних для {0} точек нет.
Задача 4.
Что можно сказать о непрерывности отображения f : (R, τ) → R, если известно, что f : R → R непрерывно и τ сильнее стандартной топологии на R?
Решение задачи 4.
Поскольку f : R → R — непрерывно, для любого открытого множества U из стандартной топологии на R прообраз f−1(U) открыт в стандартной топологии.
22 |
Методические указания по выполнению самостоятельной работы |
Поскольку τ сильнее стандартной топологии на R, любое множество, открытое в стандартной топологии, открыто и в τ. Следовательно, f : (R, τ) → R —
непрерывное отображение.
Задача 5.
Пусть T1 = (X1, τ1), T2 = (X2, τ2) — два топологических пространства, а g
— отображение X1 в X2. Тогда g называется открытым, если из того, что A τ1 g(A) τ2, и замкнутым, если из того, что A′ X \τ1 g(A′) X \τ2. Существует ли непрерывное отображение T1 в T2, не являющееся ни открытым, ни замкнутым?
Решение задачи 5.
Ответ: Да.
Пусть функция g(x) = ex cos x задана на R1, где определена обычная топология. Легко видеть, что g отображает R1 в R1 непрерывно, однако образ открытого множества (−∞; 0) не является открытым; множество g({−nπ : n = 1, 2, . . . })
не является замкнутым.
Задача 6.
Доказать, что шар B ={x Rn : x < 1} гомеоморфен пространству Rn.
Решение задачи 6.
Требуемый гомеоморфизм f : Bn → Rn осуществляет, например, отображение
f: x = (x1, . . . , xn) → p · (x1, . . . , xn), где p = tg (π/2 · x ) .
Всамом деле, f инъективно: f сохраняет направления, поэтому если x′ ̸= x′′, но x′ = x′′ , то f(x′) ̸= f(x′′). Но f также сюрьективно: f принимает все
направления, а при выбранном направлении q, т.е. вектора единичной длины
q = 1, значения |
π |
|
|
||
f(tq) = t tg( |
|
t) · q, t (−1, 1) |
2 |
||
пробегают все значения с направлением q.
Топология |
23 |
Задача 7.
Какие множества прямой могут быть непрерывными образами множества M
точек плоскости, у которых по крайней мере одна из координат рациональная?
Решение задачи 7.
Множество M связно, поэтому любой непрерывный образ этого множества связен. На прямой всякое связное множество имеет вид (α, β), (α, β], [α, β), либо [α, β], где −∞ ≤ α ≤ β ≤ +∞. Покажем, что каждое из этих множеств есть непрерывный образ M. Отображение f : M −→ R, f(x) = ρ(x, a0) (расстояние от a0 до x), где a0 = (π, π) переводит M в (0, +∞), а так как все интервалы прямой гомеоморфны друг другу, то каждый интервал есть образ M. Рассматривая композицию отображения M на всю прямую R и отображения x −→ |x|, получим непрерывное отображение M на [0; +∞), так что любой полуинтервал
— образ M. Композиция отображения M на R и отображения f(x) = sin x отображает M на [-1;1], так что любой отрезок — образ M. Наконец, отображение f, переводящее каждую точку M в константу d, непрерывно, так что каждая точка (т.е. множество [α, α]) — образ M.
Задача 8.
Верно ли, что образ несвязного пространства при непрерывном отображении является пространством несвязным?
Решение задачи 8.
Ответ: неверно.
Рассмотрим пространство X = (−1/2, 0) (3/2, 2] с топологией, индуцированной стандартной топологией на R и определим отображение из X в интервал
(−1, 1) по правилу:
2y, если −1/2 < y < 0;
f(y) =
4 − 2y, если 3/2 < y 6 2.
Это отображение взаимно однозначно, и, очевидно, непрерывно.
24 |
Методические указания по выполнению самостоятельной работы |
§4. Пример контрольной работы для промежуточного контроля
№1.
Вариант 1: Что можно сказать о непрерывности отображения f : R →
(R, τ), f : x → 0, если топология τ на R не сравнима со стандартной (метрической)топологией на R?
Вариант 2: Что можно сказать о непрерывности отображения f : R → (R, τ), f : x → 0, если топология τ на R сильнее, чем стандартная (метрическая)топология
на R?
Вариант 3: Что можно сказать о непрерывности отображения f : R → (R, τ), f : x → 0, если топология τ на R слабее, чем стандартная (метрическая)топология
на R?
№2. Пусть X = ({a, b, c, d}, τ1), Y = ({p, q, r, m}, τ2) — множества из четырех точек с заданными на них топологиями, f : X → Y — непрерывное отображение. Привести пример f, τ1, τ2 так, чтобы
Вариант 1: отображение f было открытым и замкнутым;
Вариант 2: отображение f было не открытым и замкнутым;
Вариант 3: отображение f было открытым и не замкнутым.
№3.
Вариант 1: Сформулируйте утверждение об открытости и замкнутости непрерывного отображения f, если f — биекция. Приведите примеры к своему утверждению.
Вариант 2: Приведите пример открытого, не замкнутого, не непрерывного отображения.
Вариант 3: Приведите пример не открытого, замкнутого, не непрерывного
отображения.
№4.
Докажите, что τi, i = 1, 2, 3 — топология на R.
Вариант 1: τ1 = R (−∞, 0) {Uα = R \ {aα1 , . . . , aαp }}, ai > 0.
Вариант 2: τ2 = (−∞, 0) (−∞, 0] {0} [0, ∞) (0, ∞) R \ {0} .
Топология |
25 |
Вариант 3: τ3 = R {Uα = R \ {aα1 , . . . , aαp }}.
Какие из этих топологий не могут быть порождены никакой метрикой? Приведите несколько примеров замкнутых множеств в τi. Приведите свой пример топологии на R.
№5.
Самый простой пример разрывной функции на R в матанализе — это функция f(x) = signx (принимает значения 1, при x > 0, −1 при x < 0 и 0 при x = 0). Рассмотрим отображение signx : X = (R, τ) → Y , где Y = {−1, 0, 1} с
топологией, индуцированной при помощи стандартной (метрической) топологии на R. Нарисуйте график. В какой из топологий τi из предыдущего задания это отображение непрерывно? Придумайте аналогичный пример.
№6.
Докажите, что отображение полуотрезка (0, 2π] в окружность x2 + y2 = 1 по правилу x = cos t, y = sin t не является гомеоморфизмом. (Указание: используйте утверждение о непрерывном отображении связных множеств).
№7.
Приведите свой пример непрерывного, но не изометричного отображения метрических пространств. Приведите свой пример изометричного отображения метрических пространств. Является ли это отображение непрерывным?
№8.
Привести пример счетного нигде не плотного в R множества. Будет ли это множество нигде не плотным, всюду плотным в X = (R, τi), если
Вариант 1: i = 1; Вариант 2: i = 2; Вариант 3: i = 3.
№9.
Может ли фактор-пространство хаусдорфова пространства быть нехаусдорфовым? (Рассмотрите пару параллельных прямых в R2, склейте их по открытому лучу).
№10.
Докажите, что подмножество рациональных чисел Q R не связно. Сохранится ли свойство несвязности, если на R ввести топологию τi:
Вариант 1: i = 1; Вариант 2: i = 2; Вариант 3: i = 3.

Методические указания по выполнению самостоятельной работы
26
Образец тестовых заданий для итогового |
контроля |
§5. |
|
ТОПОЛОГИЯ ФИО_______________________________ГРУППА________ ДАТА «____»________20____ БАЛЛ 


|
|
ЗАМКНУТЫ В |
|
ОТКРЫТЫ В |
|
|
ТОПОЛОГИИ КОНЕЧНЫХ |
|
СТАНДАРТНОЙ ТОП ОЛОГИИ |
|
ДОПОЛНЕНИЙ НА |
НА |
||
|
|
|
||
|
|
|
|
|
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО, СОДЕРЖАЩЕЕ СЧЕТНОЕ ВСЮДУ
ПЛОТНОЕ МНОЖЕСТВО, ЭТО ___________ ___ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО , В КОТОРОМ ЛЮБЫЕ ДВЕ ТОЧКИ
РАЗДЕЛЯЮТСЯ НЕ ПЕРЕСЕКАЮЩИМИС Я ОКРЕСТНОСТЯМИ, ЭТО
______________ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО
ЕСЛИ f— ОТОБРАЖЕНИЕ ИЗ ТОПОЛ ОГИЧЕСКОГО ПРОСТРАНСТВА X
В НЕКОТОРОЕ МНОЖЕСТВО Y, ТО ТОПОЛОГИЯ, ВВЕДЕННАЯ НА Y ТАК, ЧТО ОТОБРАЖЕНИЕ f C (X, Y), НАЗЫВАЕТСЯ ТОПОЛОГИЕЙ, ______________
ОТОБРАЖЕНИЕМ f:

 ОТОБРАЖЕНИЯ ВИДА f : X → R НАЗЫ ВАЮТСЯ _______________ НА X:
ОТОБРАЖЕНИЯ ВИДА f : X → R НАЗЫ ВАЮТСЯ _______________ НА X:
ОДНИМИ И ТЕМИ ЖЕ ТОПОЛОГИЧЕСКИМИ СВОЙСТВАМИ ОБЛАДАЮТ
_________________ ПРОСТРАНСТВА
ТОПОЛОГИЧЕСКОЕ
ПРОСТРАНСТВО С МЕТРИЧЕСКОЙ ТОПОЛОГИЕЙ ЯВЛЯЕТСЯ: сепарабельным 
пространством с I аксиомой счетности 

пространством со II аксиомой счетности
для любой его точки существует фундаментальная система окрестностей 
ЕСЛИ A–ЗАМКНУТОЕ
МНОЖЕСТВО, М ОТКРЫТОЕ МНОЖЕСТВО, ТО МНОЖЕСТВО A\М ОБЯЗАТЕЛЬНО ЯВЛЯЕТСЯ. . .
открытым
замкнутым
ни открытым, ни замкнутым 
открытым и замкнутым одновременно
ПОСЛЕДОВАТЕЛЬНОСТЬ
ТОПОЛОГИЙ НА ЧИС ЛОВОЙ ПРЯМОЙ, НАЧИНАЯ С НАИБОЛЕЕ СЛАБОЙ ( В ПОРЯДКЕ УСИЛЕНИЯ):
ЕСЛИ A–ЗАМКН УТОЕ
МНОЖЕСТВО, М ОТК РЫТОЕ МНОЖЕСТВО, ТО МН ОЖЕСТВО М\А ОБЯЗАТЕЛЬНО Я ВЛЯЕТСЯ . . открытым
з  амкнутымни открытым, ни замкнутым открытым и замкнутым
амкнутымни открытым, ни замкнутым открытым и замкнутым
одновременно
ОТОБРАЖЕНИЕ 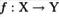 ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА X В ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО Y ЯВЛЯЕТСЯ НЕПРЕРЫВНЫМ, ЕСЛИ ПРООБРАЗ КАЖДОГО:
ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА X В ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО Y ЯВЛЯЕТСЯ НЕПРЕРЫВНЫМ, ЕСЛИ ПРООБРАЗ КАЖДОГО:
замкнутого в Y множества замкнут в X открытого в Y множества открыт в X  замкнутого в Y множества открыт в X
замкнутого в Y множества открыт в X 
 открытого в Y множества замкнут в X
открытого в Y множества замкнут в X
КОМПОЗИЦИЯ ДВУХ
НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ ЯВЛЯЕТСЯ . . .
гомеоморфизмом непрерывным отображением взаимно однозначным гомоморфизмом
СООТВЕТСТВИЕ МЕЖДУ
ГОМ ЕОМОРФНЫМИ МНОЖЕСТВАМИ В 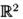 С ЕСТЕСТВЕННОЙ ТОПОЛОГИЕЙ:
С ЕСТЕСТВЕННОЙ ТОПОЛОГИЕЙ:
ОТОБРАЖЕНИЕ f ИЗ
ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА X В ТО ПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО Y ОБЯЗАТЕЛЬНО БУДЕТ НЕПРЕРЫВНЫМ, ЕСЛИ:
на X введена дискретная топология на Y введена дискретная топология на X введена тривиальная топология на Y введена тривиальная топология

27
Топология
ГОМЕОМОРФНОЕ
ОТОБРАЖЕНИЕ f ИЗ R С ЕСТЕСТВЕННОЙ ТОПОЛОГИЕЙ В СЕБЯ ЯВЛЯЕТСЯ: непрерывным
дифференцируемым взаимно однозначным обратимым биекцией
 В МНОЖЕСТВЕ C (X, Y)
В МНОЖЕСТВЕ C (X, Y)
ТЕМ БОЛЬШЕ ЭЛЕМЕНТОВ, ЧЕМ:
слабее топология на X сильнее топология на X слабее топология на Y сильнее топология на Y
МНОЖЕСТВО
НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ ИЗ X В Y ОБОЗНАЧАЮТ СИМВОЛОМ:
МНОЖЕСТВА,
ГОМЕОМОРФНЫЕ ИНТЕРВАЛУ (0, 1) ЧИСЛОВОЙ ПРЯ МОЙ 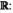 С ЕСТЕСТВЕННОЙ ТОП ОЛОГИЕЙ
С ЕСТЕСТВЕННОЙ ТОП ОЛОГИЕЙ
НЕПРЕРЫВНЫМ Я ВЛЯЕТСЯ
ВСЯКОЕ:
гомеоморфное отображение постоянное отображени е сжимающее отображение
взаимно однозначное отображение
тождественное отображ ение
НЕПРЕРЫВНАЯ ФУНКЦИЯ f(x) МОЖЕТ ПЕРЕВЕС ТИ ИНТЕРВАЛ (0, 1) В:
СООТВЕТСТВИЕ МЕЖДУ ОТОБРАЖЕНИЯМИ И
ПРОСТРАНСТВАМИ, ТОПОЛОГИИ КОТОРЫХ ОНИ ОПР ЕДЕЛЯЮТ:
индуцированное |
факторпространство |
|
отображение |
топологическое произвед ение |
|
|
||
отображение |
пространств |
|
топологическая сумма |
||
проектирования |
||
каноническое |
пространств |
|
подпространство |
||
отображение |
||
|
||
|
|
ОТОБРАЖЕНИЕ f ИЗ ДИСКРЕТНОГО
ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА X В ПРОИЗВОЛЬНОЕ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО Y ОБЯЗАТЕЛЬНО ЯВЛЯЕТСЯ . . .
гомеоморфизмом непрерывным открытым замкнутым
СООТВЕТСТВИЕ МЕЖДУ
ГОМЕОМОРФНЫМИ МНОЖЕСТВАМИ НА ЧИСЛОВОЙ ПРЯМОЙ С ЕСТЕСТВЕННОЙ ТОПОЛОГИЕЙ:
ОБРАЗ СВЯЗНОГО МНОЖЕСТВА
ПРИ НЕПРЕРЫВНОМ ОТОБРАЖЕНИИ:
есть обязательное связное множество может быть связным множеством может быть несвязным множеством иногда бывает связным множеством
ОТОБРАЖЕНИЕ f ИЗ ПРОИЗВОЛЬНОГО
ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА X В ДИ СКРЕТНОЕ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО Y ОБЯЗАТЕЛЬНО ЯВЛЯЕТСЯ:
гомеоморфизмом непрерывным открытым замкнутым
ЕСЛИ f — НЕПРЕРЫВНАЯ ФУНКЦИЯ,
ОПРЕДЕЛЕННАЯ НА ТОПОЛОГИЧЕСКОМ ПРОСТРАНСТВЕ X, ТО МНОЖЕСТВО
 ВСЕГДА . . .
ВСЕГДА . . .
открыто замкнуто сост оит из одной точки счет но
ЕСЛИ f — НЕПРЕРЫВНАЯ ФУНКЦИЯ,
ОПРЕДЕЛЕННАЯ НА ТОПОЛОГИЧЕСКОМ ПРОСТРАНСТВЕ X, ТО МНОЖЕСТВО
 ВСЕГДА . . .
ВСЕГДА . . .
открыто замкнуто бесконечно пусто
БАЗОЙ ТОПОЛОГИЧЕСКОГО ПРОСТРАНСТВА (X, τ ) НАЗЫВАЕТСЯ ТАКОЕ
СЕМЕЙСТВО P ОТКРЫТЫХ МНОЖЕСТВ ИЗ (X , τ ), ЧТО ЛЮБОЕ ОТКРЫТОЕ МНОЖЕСТВО ИЗ (X, τ ) ЯВЛЯЕТСЯ __________ ____ НЕКОТОРОГО ПОДСЕМЕЙСТВА ИЗ P
ЕСЛИ ДВЕ ЛЮБЫЕ ТОЧКИ ПРОСТРАНСТВА ОБЛАДАЮТ
НЕПЕРЕСЕКАЮЩИМИСЯ ОКРЕСТНОСТЯМИ, ТО ПРОСТРАНСТВО НАЗЫВАЕТСЯ
_____________________.
Учебное издание
ТОПОЛОГИЯ
О.В. Знаменская
Подготовлено к изданию РИО БИК СФУ Компьютерная верстка: О.В. Знаменской
Подписано в печать 31.08.2012 г. Формат 60x84/16. Бумага офсетная. Печать плоская.
Усл. печ. л. 1,5. Уч.-изд. л. 1 Тираж 50 экз. Заказ № ????.
Редакционно-издательский отдел Библиотечно-издательского комплекса Сибирского федерального университета 660041, г. Красноярск, пр. Свободный, 79 Тел/факс (391) 201-21-49. E-mail rio@sfu-kras.ru http://rio.sfu-kras.ru
Отпечатано Полиграфическим центром Библиотечно-издательского комплекса Сибирского федерального университета 660041, г. Красноярск, пр. Свободный, 82а
