Вычисление определенного интеграла

Можно указать 4 способа вычисления определенного интеграла:

1. по определению (как предел интегральной суммы);

2. приближенно (по формулам прямоугольников, трапеций, Симпсона);

3. по формуле Ньютона-Лейбница;

4. используя программные пакеты (Matcad, и т.д.).

Примеры вычисления ОИ по определению и приближенно вы можете найти учебнике Н.С. Пискунова «Дифференциальное и интегральное исчисления». С использованием программных пакетов вы познакомитесь на занятиях по специальным дисциплинам.

Мы рассмотрим вычисление ОИ по формуле Ньютона-Лейбница. Эта формула имеет вид

= =F(b) –F(a),

где - первообразная для функции. Формула Ньютона-Лейбница дает простое правило для вычисления определенного интеграла от непрерывной на заданном отрезке функции, позволяя свести вычисление предела интегральной суммы к отысканию первообразной от заданной функции и вычислению разности ее значений на концах отрезка интегрирования. Иначе говоря,определенный интеграл от заданной функции по заданному отрезку равен приращению первообразной для этой функции на заданном отрезке.

Примеры решения задач.

Пример 1.

Существуют ли определенные интегралы от заданных функций по указанным промежуткам (т.е. интегрируема ли функция на данном промежутке) ?

а) б);

в) ?

Решение. Согласно теореме 2, определенный интеграл существует, если выполняются условия:

1. функция непрерывна или кусочно-непрерывна на отрезке;

2. отрезок – конечный.

Проверим выполнение этих условий для заданных функций.

а) Функцияимеет разрыв второго рода в точке, значит, определенный интеграл от данной функции по указанному отрезку не существует.

б) Функциянепрерывна на всем промежутке, но сам промежуток – бесконечный, поэтому определенный интеграл от данной функции по указанному промежутку не существует.

в) Функциянепрерывна на всей числовой прямой, отрезок– конечный, следовательно, определенный интеграл от данной функции по указанному промежутку существует.

Пример 2.

Используя геометрический смысл определенного интеграла, установить, какой из интегралов больше или?

Решение. С геометрической точки зрения, определенный интеграл 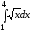численно равен площади области, расположенной между линиейи отрезкомоси Ох (криволинейной трапеции АВСD, рисунок 2), а интеграл – площади криволинейной трапеции АВС₁D₁ на том же рисунке:

.

Но, очевидно, 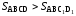, значит,>.

Пример 3.

Не вычисляя, сравните интегралы:

а) и; б)и.

Решение.

а) Воспользуемся свойством: если интегрируемые на [a,b] функции f(x) и g(x) удовлетворяют неравенству f(x)  g(x), то

.

Сравним функции ина отрезке интегрирования. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. Очевидно,для любого, поэтому<. Тогда, согласно указанному свойству,<.

б) Рассмотрим и. Поскольку интегрируется одна и та же функция, но по разным промежуткам, воспользуемся геометрическим смыслом определенного интеграла. Рассмотрим площади областей ОАВ и СDОАВ между графиком функции и, соответственно, отрезкамииоси Ох (рисунок 3).

Площадь области ОАВ численно равна интегралу :. Площадь области СDОАВ равна сумме площадей областей СDО и ОАВ: . Но, а, т.к.на отрезке. Итак, имеем,. Тогда

.

Значит, >.

Пример 4.

Используя свойства определенного интеграла, упростить вычисление интеграла (не вычисляя):

а) ; б); в).

Решение.

а) Рассмотрим функцию . Легко доказать, что эта функция – четная:

.

Поскольку интегрирование ведется по промежутку , симметричному относительно начала координат, то можно воспользоваться свойством интегралов:если f(x) четная функция, то . Следовательно, в нашем случае,.

б) В интеграле подынтегральная функция, как известно, нечетная, а промежуток интегрированиясимметричен относительно нуля, поэтому можно воспользоваться свойством:если f(x) нечетная функция, то . Тогда.

в) Рассмотрим интеграл . Подынтегральная функцияесть периодическая функция^*)с периодом. Действительно,

.

Кроме того, длина отрезка интегрирования равна :

^**).

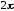Поэтому вычисление данного интеграла можно упростить, воспользовавшись свойством: если f(x) периодическая функция с периодом Т, то .

Тогда =.

Пример 5. Вычислить определенные интегралы:

а) ; б); в);

г) ;д); е).

Решение.

а) Как уже отмечалось выше, вычисление определенного интеграла с помощью формулы Ньютона-Лейбница

= =F(b) –F(a)

сводится к отысканию первообразной (неопределенного интеграла) и вычислению разности ее значений на концах интервала. Поэтому все приемы нахождения неопределенного интеграла, с небольшими поправками, переносятся на случай вычисления определенного интеграла.

.

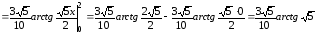б)

.

в)

.

г)

.

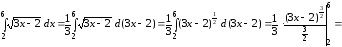
д)

.

е)

.

Пример 6. Вычислить определенный интеграл, если

Решение.

Подынтегральная функция на отрезке интегрированиязадана разными аналитическими выражениями:

х

0

е

1

3

Поэтому, используя свойство 6 определенного интеграла, преобразуем

.