
FAIT1 / Интегралы-Помощь / Определенный интеграл / 3. Приложения ОИ
.docxПриложения определенного интеграла
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
а) Площадь фигуры
Как
уже отмечалось,
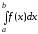 численно равен площади криволинейной
трапеции, ограниченной кривой у =
f(x),
f(x)
≥ 0, прямыми х = а, х = b
и отрезком [a, b]
оси ОХ (рисунок 1).
численно равен площади криволинейной
трапеции, ограниченной кривой у =
f(x),
f(x)
≥ 0, прямыми х = а, х = b
и отрезком [a, b]
оси ОХ (рисунок 1).
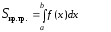 (1)
(1)


Учитывая свойства определенного интеграла, эту геометрическую интерпретацию можно обобщить и на случай f(x) 0(рис.2). А именно, если f(x) 0 на [a, b] , то
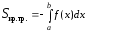 (2)
(2)
Т.е. площадь криволинейной трапеции, расположенной под осью ОХ, равна соответствующему интегралу, взятому со знаком минус.
Если же на заданном отрезке функция у = f(x) меняет знак, то для вычисления площади фигуры, заключенной между графиком этой функции и осью ОХ, следует разбить отрезок на части, на каждой из которых функция сохраняет знак, и найти площадь каждой части фигуры. Искомая площадь в этом случае есть алгебраическая сумма интегралов по этим отрезкам, причем интегралы, соответствующие отрицательным значения функции, взяты в этой сумме со знаком минус (рис.3):

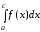 –
–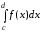 +
+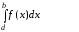 (3)
(3)

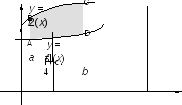
Если
фигура ограничена двумя кривыми у
= f1(x)
и у = f2(x),
f1(x)
f2(x)
то, как следует из рисунка 4, ее площадь
равна разности площадей криволинейных
трапеций аВСb и
аАDb
, каждая из которых численно равна
интегралу. Значит,
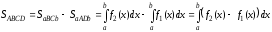 .
.
Таким
образом,
 (4)
(4)
 Заметим,
что площадь фигуры, изображенной на
рисунке 5а, находятся по такой же формуле:
Заметим,
что площадь фигуры, изображенной на
рисунке 5а, находятся по такой же формуле:
S
=

(докажите это!). Подумайте, как вычислить площадь фигуры, изображенной на рисунке 5б?

Мы вели речь только о криволинейных трапециях, прилежащих к оси ОХ. Но аналогичные формулы справедливы и для фигур, прилежащих к оси ОУ. Например, площадь фигуры, изображенной на рисунке 6а, находится по формуле
S
=
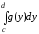 .
(5)
.
(5)
 Если
область ограничена двумя линиями
Если
область ограничена двумя линиями
 ,
,
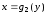 и прямыми
и прямыми
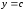 ,
,
 (рисунок
6б), то площадь этой области можно найти
по формуле
(рисунок
6б), то площадь этой области можно найти
по формуле
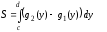 (6)
(6)
Если
линия, ограничивающая криволинейную
трапецию, задана параметрическими
уравнениями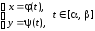 ,
то площадь этой криволинейной
трапеции равна
,
то площадь этой криволинейной
трапеции равна
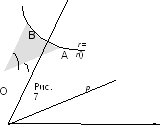
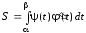 .
(7)
.
(7)
Рассмотрим полярную систему координат. Фигура ОАВ, ограниченная лучами =, = и кривой r = r() (рисунок 7) называется криволинейным сектором. Площадь криволинейного сектора ОАВ находится по формуле
S
=
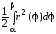 (8)
(8)
б) Длина дуги кривой
Пусть дана кривая у=f(x). Рассмотрим дугу (рисунок 8а). Длина этой дуги кривой находится по формуле
l
=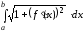 .
(9)
.
(9)
Если
кривая задана уравнением
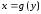 ,
и рассматривается дуга
,
и рассматривается дуга
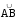 этой кривой, соответствующая изменению
у на отрезке [с, d]
(рисунок 8б), длина этой дуги может быть
найдена по формуле
этой кривой, соответствующая изменению
у на отрезке [с, d]
(рисунок 8б), длина этой дуги может быть
найдена по формуле
l
=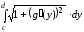 .
(10)
.
(10)

б)
Если
кривая задана параметрически
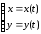 ,
то длина дуги этой кривой, соответствующей
изменению параметра t[,
],
находится по формуле
,
то длина дуги этой кривой, соответствующей
изменению параметра t[,
],
находится по формуле
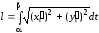 (11)
(11)
Если
дуга кривой задана в полярной системе
координат уравнением
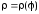 ,
[,
], то
,
[,
], то
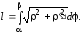 (12)
(12)
 в)
Объем тела вращения.
в)
Объем тела вращения.
Рассмотрим криволинейную трапецию аАВb , ограниченную линией у = f(x), прямыми х = а, х = b и отрезком [a, b] оси ОХ (рис.9). Пусть эта трапеция вращается вокруг оси ОХ, в результате получится тело вращения, объем которого выражается формулой

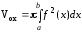 (13)
(13)
Аналогично можно записать формулу объема тела, полученного вращением вокруг оси ОУ криволинейной трапеции, ограниченной графиком функции х = (у), прямыми y = c , y = d и отрезком [c, d] оси ОУ (рис.10):
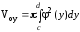 (14)
(14)
Пример 1.
Построить фигуру, ограниченную линиями, и найти ее площадь:
а)
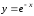 ,
,
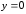 ,
,
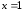 ,
,
 ;
б)
;
б)
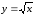 ,
,
 ,
,
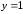 ,
,
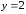 ;
;
в)
 ,
,
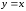 ;
г)
;
г)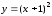 ,
,
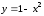 ,
,
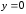 .
.
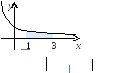 Решение.
Решение.
Рис.11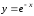 ,
,
 ,
,
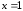 ,
,
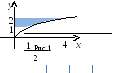
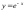 (рисунок
11). Площадь полученной криволинейной
трапеции найдем по формуле (1):
(рисунок
11). Площадь полученной криволинейной
трапеции найдем по формуле (1):
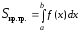 ,
где
,
где
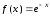 ,
,
 ,
,
 .
.
Получим
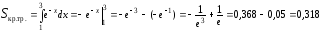 (кв.ед).
(кв.ед).
б)
Построим
линии
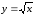 ,
,
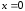 ,
,
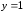 ,
,
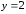 (рисунок
12). Фигура, ограниченная данными линиями,
есть криволинейная трапеция, прилежащая
к оси Оу,
поэтому для вычисления её площади
воспользуемся формулой (5): S
=
(рисунок
12). Фигура, ограниченная данными линиями,
есть криволинейная трапеция, прилежащая
к оси Оу,
поэтому для вычисления её площади
воспользуемся формулой (5): S
=
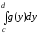 .
Здесь
.
Здесь
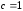 ,
,
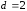 ,
а функцию
,
а функцию
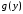 получим
из уравнения линии
получим
из уравнения линии
 ,
если выразим х
через у:
,
если выразим х
через у:
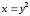 Тогда
имеем
Тогда
имеем
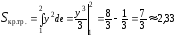 (кв.ед).
(кв.ед).
в)
Построим
линии
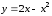 ,
,
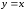 .
Линия
.
Линия
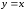 есть прямая (биссектриса I
и III
координатных углов).
есть прямая (биссектриса I
и III
координатных углов).
Линия
 есть парабола, чтобы изобразить её,
найдем вершину и точки пересечения
параболы с осями координат. Известно,
что если парабола имеет уравнение
есть парабола, чтобы изобразить её,
найдем вершину и точки пересечения
параболы с осями координат. Известно,
что если парабола имеет уравнение
 ,
то абсцисса её вершины равна
,
то абсцисса её вершины равна
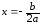 .
В случае параболы
.
В случае параболы
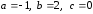 .
Тогда абсцисса вершины
.
Тогда абсцисса вершины
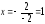 ,
а ордината
,
а ордината
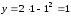 .
Таким образом, вершина параболы – точка
(1, 1). Точки пересечения параболы с осью
Ох
найдем из уравнения
.
Таким образом, вершина параболы – точка
(1, 1). Точки пересечения параболы с осью
Ох
найдем из уравнения
 :
:
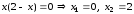 .
Значит, парабола пересекает ось Ох
в точках (0, 0) и (2, 0). Точка (0, 0) одновременно
есть точка пересечения параболы с осью
Оу.
.
Значит, парабола пересекает ось Ох
в точках (0, 0) и (2, 0). Точка (0, 0) одновременно
есть точка пересечения параболы с осью
Оу.
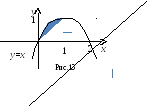 Построив
обе линии, получим область, площадь
которой требуется найти (рисунок
13).Поскольку это область, заключенная
между двумя линиями, то применим формулу
(4):
Построив
обе линии, получим область, площадь
которой требуется найти (рисунок
13).Поскольку это область, заключенная
между двумя линиями, то применим формулу
(4):
 .
.
Здесь
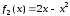 ,
,
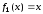 .
Границы а
и b
интервала интегрирования можно определить
по построению. А можно найти формально
как абсциссы точек пересечения данных
линий:
.
Границы а
и b
интервала интегрирования можно определить
по построению. А можно найти формально
как абсциссы точек пересечения данных
линий:
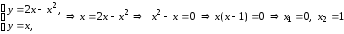 .
.
Тогда получим
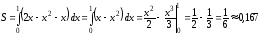 (кв.ед).
(кв.ед).
г)
Построим
линии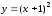 ,
,
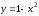 ,
,
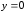 .
Линия
.
Линия
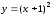 есть парабола, которая получается из
параболы
есть парабола, которая получается из
параболы
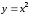 сдвигом всех точек вдоль оси Ох
на единицу влево. Парабола
сдвигом всех точек вдоль оси Ох
на единицу влево. Парабола
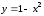 получается из параболы
получается из параболы
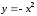 сдвигом
вдоль оси Оу
на единицу вверх. Линия
сдвигом
вдоль оси Оу
на единицу вверх. Линия
 есть
ось Ох.
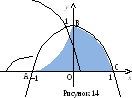
Получим область АВС, изображенную на
рисунке 14. Площадь этой области можно
найти двумя способами.
есть
ось Ох.
Получим область АВС, изображенную на
рисунке 14. Площадь этой области можно
найти двумя способами.
 1
способ.
Область
АВС есть объединение двух криволинейных
трапеций – АВО и ОВС, прилежащих к оси
Ох.
Поэтому площадь всей области равна
сумме площадей этих криволинейных
трапеций:
1
способ.
Область
АВС есть объединение двух криволинейных
трапеций – АВО и ОВС, прилежащих к оси
Ох.
Поэтому площадь всей области равна
сумме площадей этих криволинейных
трапеций:
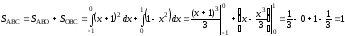 (кв.ед.)
(кв.ед.)
2 способ. Площадь области АВС можно найти по формуле (6):
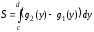 .
.
Найдем
функции
 и
и
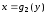 ,
графики которых ограничивают данную
область:
,
графики которых ограничивают данную
область:

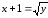
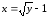
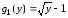 ;
;
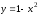
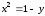
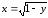
 .
.
При
этом, как видно из рисунка 14,
 .
.
Тогда
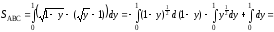
 (кв.ед.)
(кв.ед.)
Как видим, получили тот же ответ.
Пример 2.
Найти длину дуги кривой:
а)
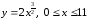 б)
б)
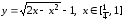 ;
;
в)
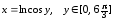 .
.
Решение.
а)
Поскольку линия задана уравнение
вида
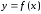 ,
воспользуемся формулой (9):
,
воспользуемся формулой (9):
l
=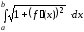 ,
,
где
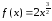 ,
,
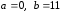 .
Но для этого сначала нужно найти
.
Но для этого сначала нужно найти
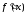 .
Имеем
.
Имеем

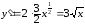 ,
,
поэтому
 .
Тогда
.
Тогда
l =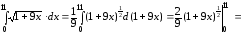
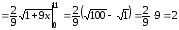 (ед.дл.).
(ед.дл.).
б)
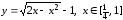 .
Здесь используем также формулу (9), считая
.
Здесь используем также формулу (9), считая
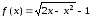 ,
,
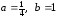 .
Находим
.
Находим
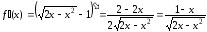 ,
,
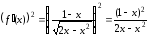 ,
,
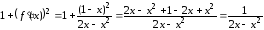 ,
,
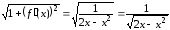 .
.
Тогда получим
l =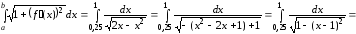
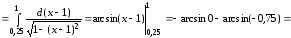
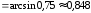 (ед.дл.)
(ед.дл.)
в)
Линия
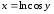 задана уравнением вида
задана уравнением вида
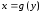 ,
поэтому используем формулу
,
поэтому используем формулу
l
=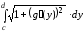 ,
,
где
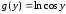 ,
,
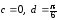 .
Находим
.
Находим
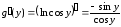 ,
,
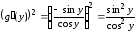 ,
,
 ,
,
 .
.
Тогда
l
=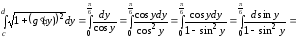
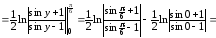
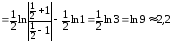 (ед.дл.)
(ед.дл.)
Пример 3.
Найти дину дуги линии:
а)
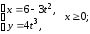 б)
б)
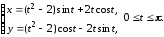
Решение.
а)
Линия задана параметрически, поэтому
будем использовать формулу (11)
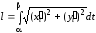 .
Заметим, что границы изменения параметра
t не указаны, но
оговорено, что дуга описывается заданными
формулами только при
.
Заметим, что границы изменения параметра
t не указаны, но
оговорено, что дуга описывается заданными
формулами только при
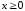 – значит, исходя из этого требования
нужно найти отрезок изменения t.
Имеем:
– значит, исходя из этого требования
нужно найти отрезок изменения t.
Имеем:
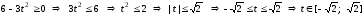 .
.
Находим

 ;
;
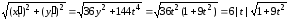 .
.
Поскольку
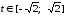 ,
то
,
то
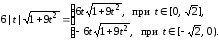
Тогда
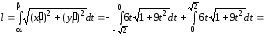
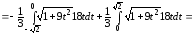
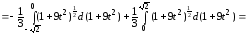

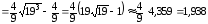 (ед.дл.).
(ед.дл.).
б)
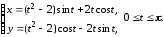 Здесь линия также задана параметрически,
значит, вновь будем использовать формулу
(11)
Здесь линия также задана параметрически,
значит, вновь будем использовать формулу
(11)
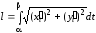 .
Найдем
.
Найдем

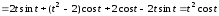 ;
;
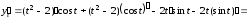
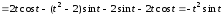 .
.
Тогда
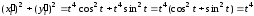 .
.
Следовательно
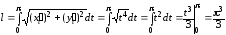 (ед.
дл.)
(ед.
дл.)
Пример 4.
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг оси Ох.
Решение.
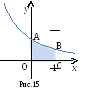 Фигура,
ограниченная линиями
Фигура,
ограниченная линиями
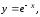
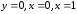 есть область ОАВС
(рисунок 15). По
формуле (13)
есть область ОАВС
(рисунок 15). По
формуле (13)
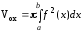 искомый объем тела, полученного в
результате вращения этой фигуры, равен
искомый объем тела, полученного в
результате вращения этой фигуры, равен
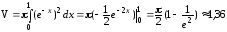 (ед.2)
(ед.2)
Пример 5.
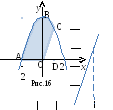
Фигура ограничена
дугой параболы
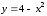 ,
отрезком
,
отрезком
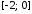 оси Ох
и отрезком прямой
оси Ох
и отрезком прямой
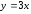 .
Найти объём тела, образованного вращением
этой фигуры вокруг оси Ох.
.
Найти объём тела, образованного вращением
этой фигуры вокруг оси Ох.
Фигура,
ограниченная дугой параболы
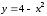 ,
отрезком
,
отрезком
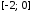 оси Ох и отрезком прямой
оси Ох и отрезком прямой
 ,
изображена на рисунке 16. Найдем абсциссу
точки С пересечения параболы
,
изображена на рисунке 16. Найдем абсциссу
точки С пересечения параболы
 с прямой
с прямой
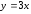 :
:
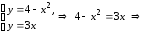
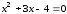
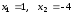 .
.
Следовательно,
С(1,3). Искомый объем равен разности
объёмов V1 и V2
тел, образованных вращением криволинейной
трапеции АВСD и треугольника
ОСD. По формуле (13)
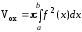 находим:
находим:
V1=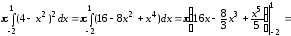
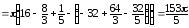 ,
,
V2 .
.
Тогда искомый объем равен
V1
– V2 =
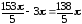 (куб.ед).
(куб.ед).
