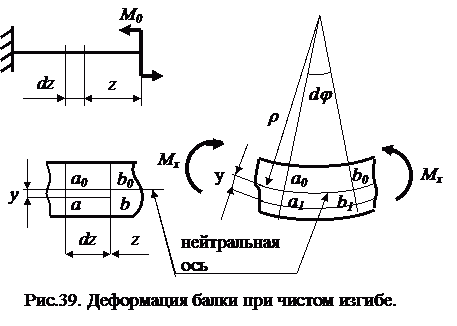
Нормальные напряжения при чистом изгибе прямого бруса

Рассмотрим случай чистого изгиба балки и выведем формулу для определения нормальных напряжений для данного случая.        Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые допущения.

Таких гипотез при изгибе три:

1) Гипотеза плоских сечений (гипотеза Бернулли)

сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной   осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.

Связь между внутренними усилиями и нормальными напряжениями в сече­нии балки найдем из рассмотрения напряжений из элементарной площадке dA, выделенной в поперечном сечении А балки в точке с координатами у и x (ось y для удобства анализа направлена вниз):

, следовательно , поэтому

;                 (6.10)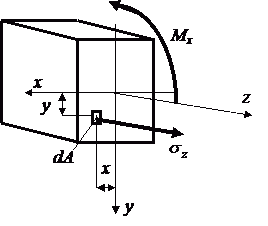

, следовательно , поэтому

 ;             (6.11)

, следовательно , поэтому

;          (6.12)

Рис.38. Напряжения при чистом изгибе

Как видим, неизвестен характер распределения нормальных напряже-ний по сечению. Для решения задачи рассмотрим геометрическую картину деформаций.

Рассмотрим деформацию элемента балки длиной dz, выделенного из изги­баемого стержня в произвольной точке с координатой z. Учитывая принятую ранее гипотезу плоских сечений, после изгиба сечения балки повернутся относительно   нейтральной   оси   (н.о.)   на угол  , при этом волокно ab, отстоящее от оси на расстояние у, превратится в дугу окружности a1b1, а его длина изменится на некоторую величину.

 

 

 

 

 

 

 

 

 

 

 

Здесь напомним, что длина волокон, лежащих на нейтральной оси, не изменяется а потому дугаa0b0 (радиус кривизны которой обозначим ), имеет ту же длину, что и отрезок a0b0 до деформации:a0b0=dx.

Найдем относительную линейную деформацию , волокна ab изогнутой бал­ки: , следовательно

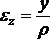                                               (6.13)

Учитывая, что, в соответствии с гипотезой об отсутствии боковых давлений, запишем закон Гука для изгиба в виде:

                                       (6.14)

Из формулы для относительной линейной деформации с учетом закона Гука получим закон распределения нормаль­ных напряжений по сечению балки:

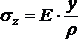.                                       (6.15)

Подставляя это выражение в каждое из уравнений равновесия, имеем следующие соотно­шения:

, следовательно , отсюда

;                                             (6.16)

, следовательно , отсюда

     ;                                                (6.17)

, следовательно , отсюда

.                                    (6.18)

Из анализа первого и второго полученных выражений следует, что оси у и х являются главными центральными осями сечения, а нейтральная ось прохо­дит через центр тяжести сечения.

Из последнего равенства получим формулу для определения кривизны бруса при изгибе

,                                      (6.19)

Используя это выражение, получим формулу определения нормальных напряжений при изгибе:

                                               (6.20)

Из анализа полученного уравнения следует, что нормальные напряжения при изгибе равны нулю в точках, лежащих на нейтральной оси, и достигают экс­тремальных значений на поверхности балки, при .

Максимальные нормальные напряжения при изгибе найдем по формуле:

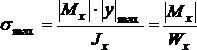,                                  (6.21)

 где     Wz -  осевой момент сопротивления

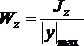                                      (6.22)

Таким образом, в случае изгиба условие прочности   по   нормальным   напряжениям   может быть записано в следующем виде (для материала балки, одинаково сопротивляющегося растяжению-сжатию):

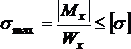
Ответ на 27) Расчёты на прочность при изгибе

Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре  наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.

Условие прочности при изгибе по нормальным напряжениям: ,

где допускаемое напряжение принимается, как и при растяжении (сжатии) стержня из такого же материала.

Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: .

При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон , расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на , в три раза, так как . В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерциипоперечного сечения стержня».