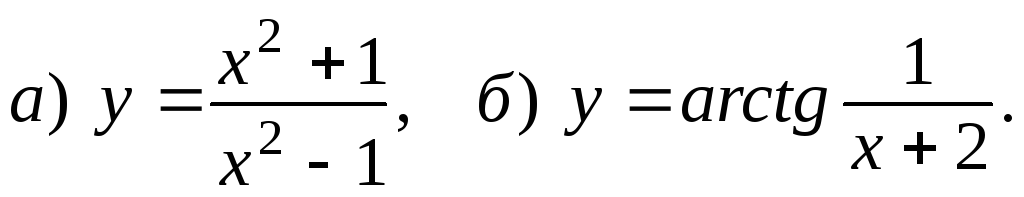Вариант 1
Обязательные задачи:
Дайте определение функции. Приведите примеры функций, заданных аналитически; графически.
Вычислите значения функций: а)
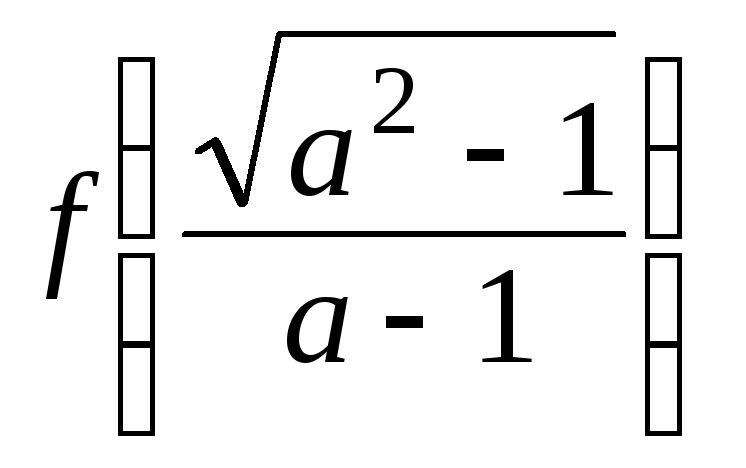 ;
если
;
если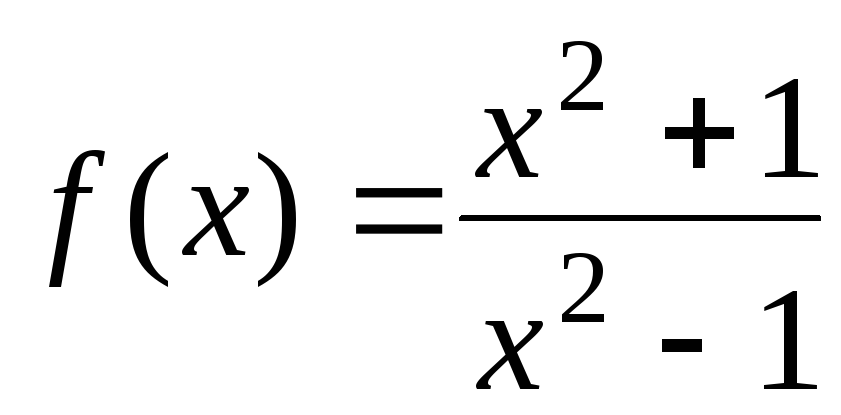 .
.
б) f(0) , f(7) , f(–12) , если f(x) = sin(3x/2) + 5cos(3x/4) .
Что понимают под областью определения функции
 ?
Что называется множеством значений
функции? Запишите показательную функции,
укажите область ее определения и
множество значений.
?
Что называется множеством значений
функции? Запишите показательную функции,
укажите область ее определения и
множество значений.Дайте определение четной, нечетной функции. Приведите пример нечетной функции.
Найдите область определения функции, и исследуйте ее на четность (нечетность):
а)
![]() б)
б)![]() ;
в)
;
в)![]() .
.
Сложную функцию записать в виде цепочки основных элементарных функций:
а)
![]() ,
б)
,
б)![]() .
.
Дайте определение графика функции. Постройте графики функций, используя преобразования графиков:
а)
![]() б)
б)![]() в)
в)
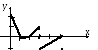 Дайте
определение периодической функции.
Приведите аналитический и графический
примеры периодических функций.
Дайте
определение периодической функции.
Приведите аналитический и графический
примеры периодических функций.Периодическая функция задана графически на полупериоде. Задайте функцию аналитически на данном промежутке. Постройте: а) четное продолжение функции на 3 периода; б) нечетное продолжение на 3 периода.
Для функции
 ,
изображенной на чертеже, найдите
,
изображенной на чертеже, найдите

Вычислите пределы функций: а)
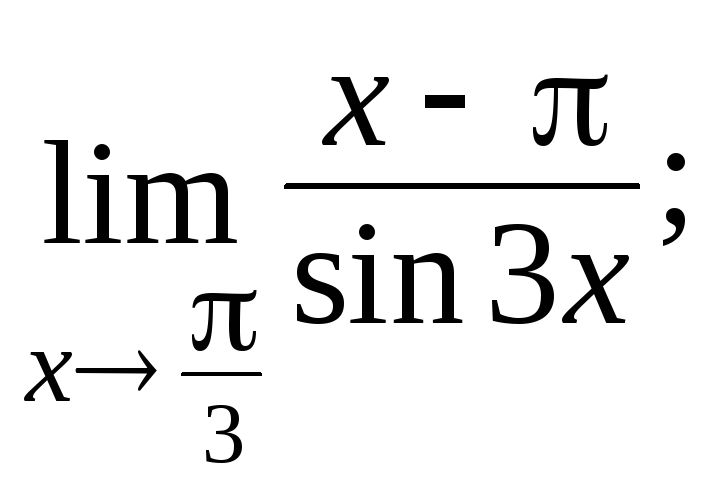 б)
б) ;
;
в)![]() г)
г)![]() д)
д)![]()
е)
![]()
![]()
Дайте определение непрерывной функции; точки разрыва второго рода. Приведите графические примеры
Исследуйте функцию на непрерывность, классифицируйте точки разрыва. Постройте график
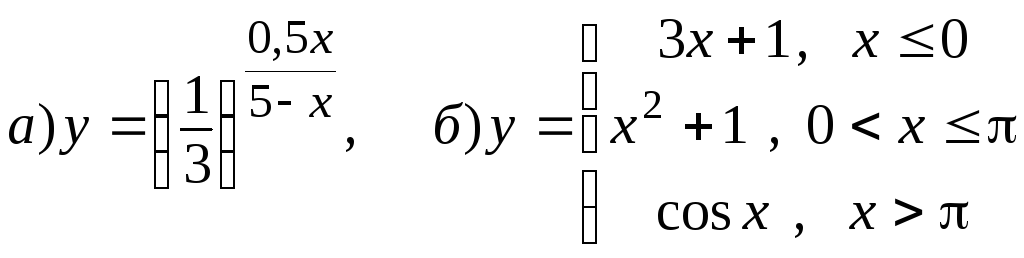
Схематически постройте график функции f(x) , удовлетворяющей условиям:
![]()
Дополнительные задачи:
Найти область определения функции
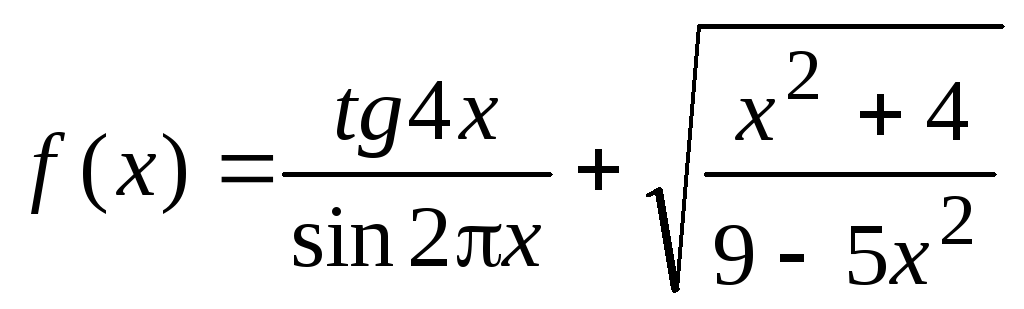 и исследовать ее на четность (нечетность).
и исследовать ее на четность (нечетность).Для функций
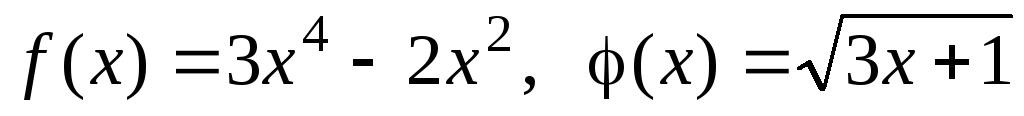 найтиf((x))
, (f(x))
,
а также области определения всех этих
функций.
найтиf((x))
, (f(x))
,
а также области определения всех этих
функций.Построить графики функций: а)
 б)
б)
Вычислить пределы
![]()
Исследуйте непрерывность функции:
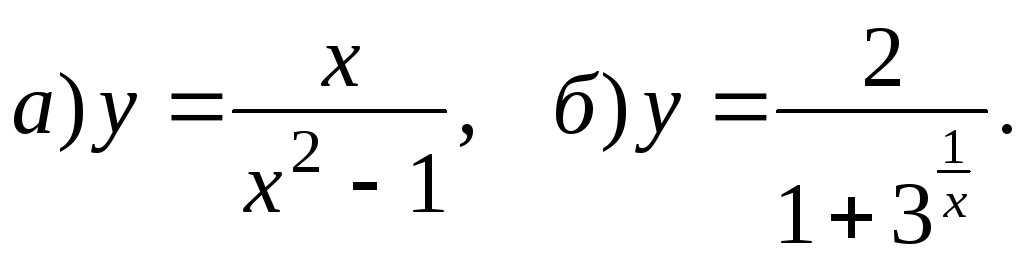
Вариант 2
Обязательные задачи:
Дайте определение функции. Приведите примеры функций, заданных аналитически; графически.
Вычислите значения функций:
![]()
Что понимают под областью определения функции
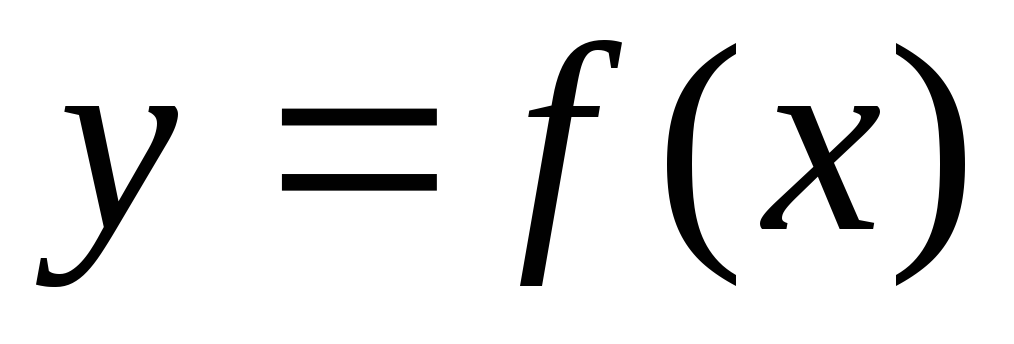 ?
Что называется множеством значений
функции? Запишите логарифмическую
функцию, укажите ее область определения
и множество значений
?
Что называется множеством значений
функции? Запишите логарифмическую
функцию, укажите ее область определения
и множество значенийДайте определение четной, нечетной функции. Приведите пример четной функции.
Найдите область определения функции, и исследуйте ее на четность (нечетность):
а)
![]() б)
б)![]() в)
в)![]() .
.
Сложную функцию записать в виде цепочки основных элементарных функций:
а)![]() ,
б)
,
б)![]() .
.
Дайте определение графика функции. Постройте графики функций, используя преобразования графиков:
а)
![]() б)
б)![]() в)
в)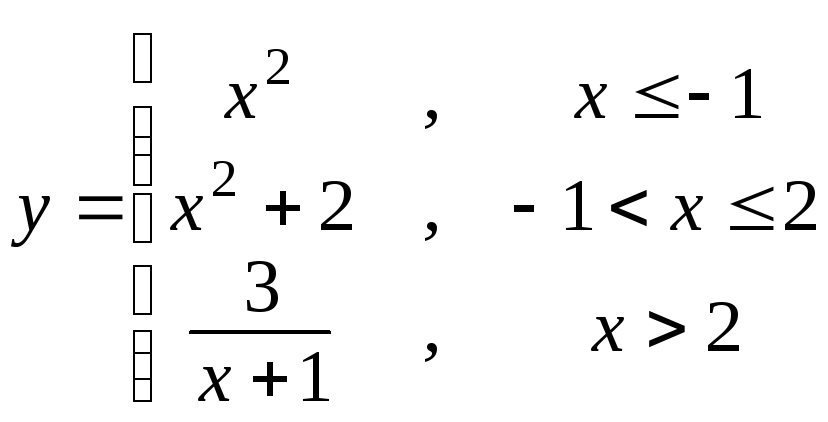
Дайте определение периодической функции. Приведите аналитический и графический примеры периодических функций.
П
 ериодическая
функция задана графически на полупериоде.
Задайте функцию аналитически на данном
промежутке. Постройте: а) четное
продолжение функции на 3 периода; б)
нечетное продолжение на 3 периода.
ериодическая
функция задана графически на полупериоде.
Задайте функцию аналитически на данном
промежутке. Постройте: а) четное
продолжение функции на 3 периода; б)
нечетное продолжение на 3 периода.Для функции
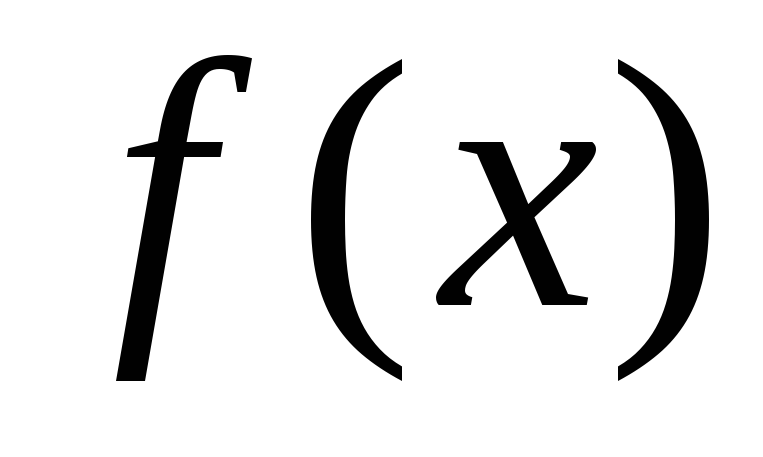 ,
изображенной на чертеже, найдите
,
изображенной на чертеже, найдите

Вычислите пределы функций: а)
 б)
б)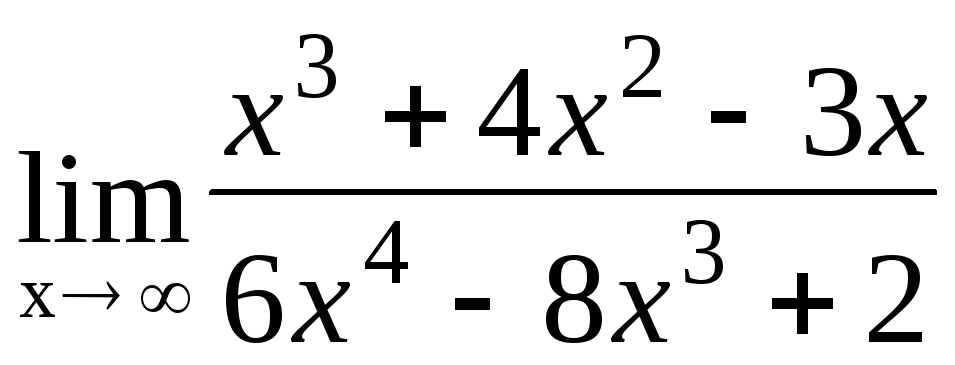 ;
в)
;
в)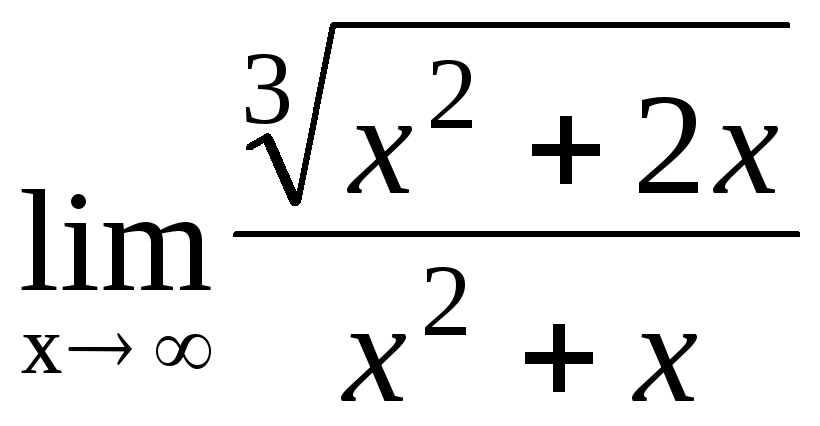
г)
![]() д)
д)![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ; з)
; з)![]() ;
и)
;
и) .
.
Дайте определение непрерывной функции; точки разрыва первого рода. Приведите графические примеры
Исследуйте функцию на непрерывность, классифицируйте точки разрыва. Постройте график
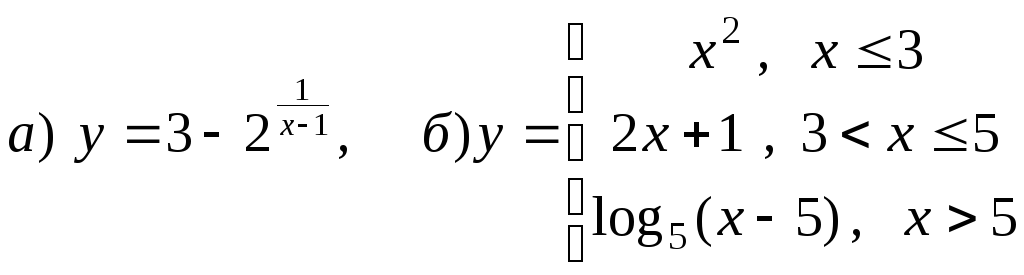
Схематически постройте график функции f(x), удовлетворяющей условиям:
![]()
Дополнительные задачи:
Найти область определения функции
 и исследовать ее на четность (нечетность).
и исследовать ее на четность (нечетность).Для функций
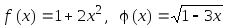 найти f((x))
, (f(x))
,
а также области определения всех этих
функций.
найти f((x))
, (f(x))
,
а также области определения всех этих
функций.Построить графики функций: а)
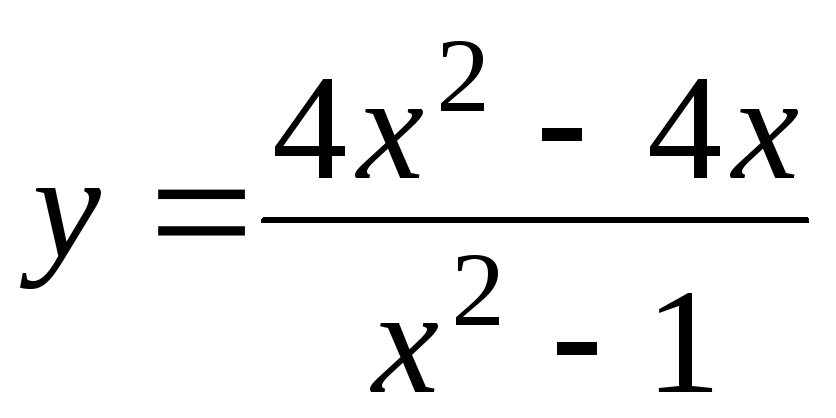 б)
б)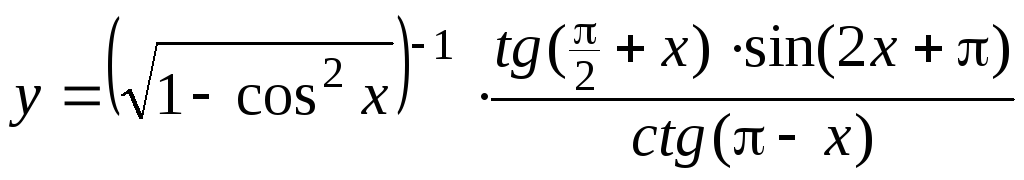
Вычислить пределы а)
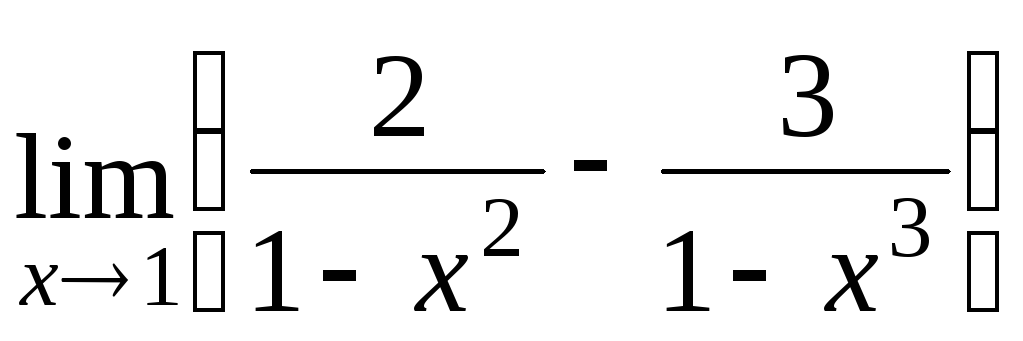 ;
б)
;
б) ;
;
![]()
Исследуйте непрерывность функции: