
Вариант 1
Составить уравнения касательной и нормали к кривой
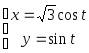
 в
точке, соответствующей
в
точке, соответствующей
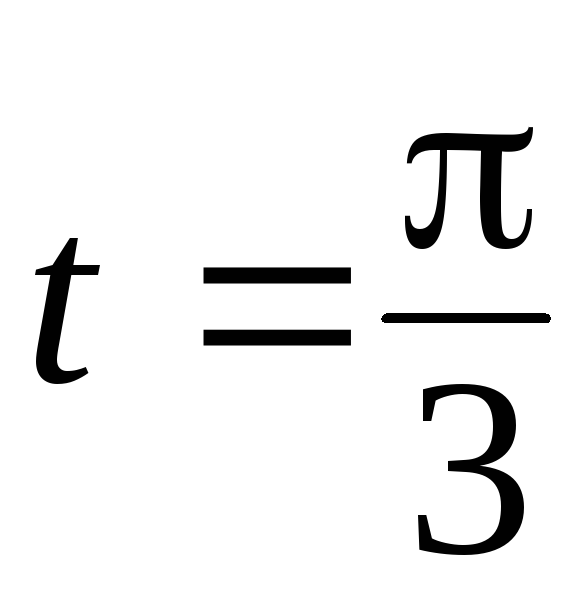 .
.Колесо вращается так, что угол поворота пропорционален кубу времени. Первый оборот был сделан колесом за время t=4 сек. Найти угловую скорость
 в моментt
=8 сек от
начала движения.
в моментt
=8 сек от
начала движения.Доказать, что для достаточно малых значений x справедлива приближенная формула
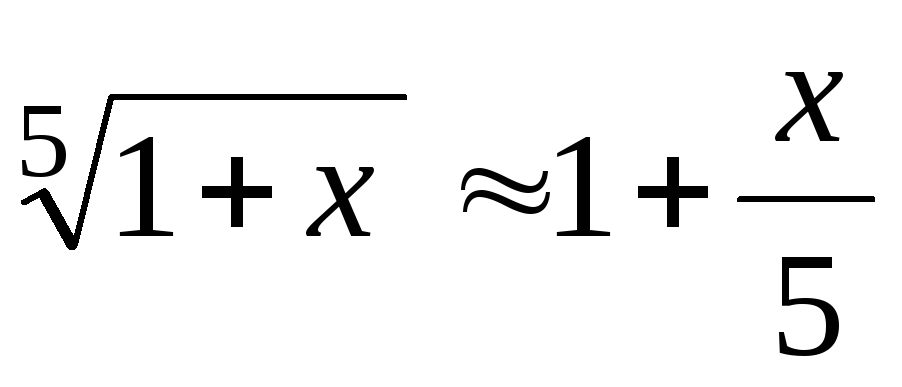
Вычислить, используя правило Лопиталя: а)
 б)
б)
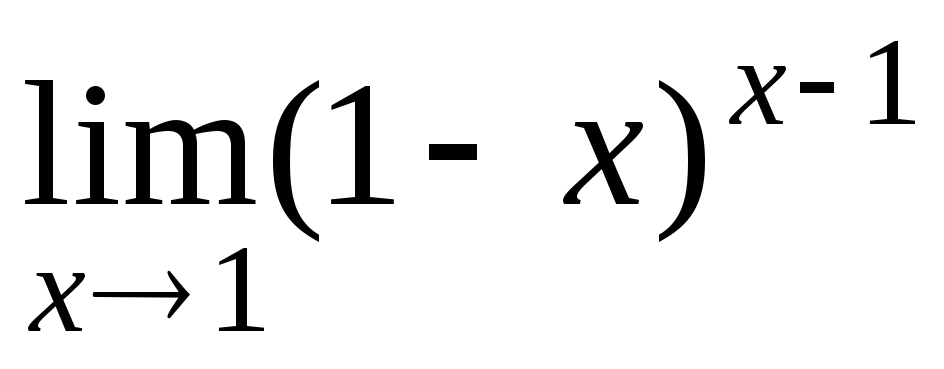
Найти асимптоты графика функции
 .
.По графику функции описать ее свойства: четность, нечетность, непрерывность, характер точек разрыва, интервалы монотонности, экстремумы, интервалы выпуклости, вогнутости, точки перегиба, уравнения асимптот.

Исследовать функцию и построить ее график:
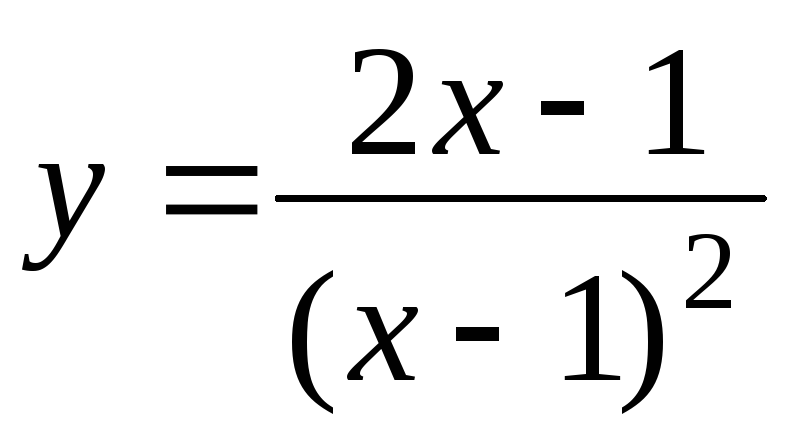 .
.Найти наибольшее и наименьшее значения функции

 на [-1,1].
на [-1,1].Стрела прогиба балки прямоугольного сечения пропорциональна произведению ширины на куб высоты этого сечения. Каковы размеры сечения балки, вырезанной из круглого бревна диаметра d, с наименьшей стрелой прогиба?
Вариант 2
Найти уравнение касательной к кривой
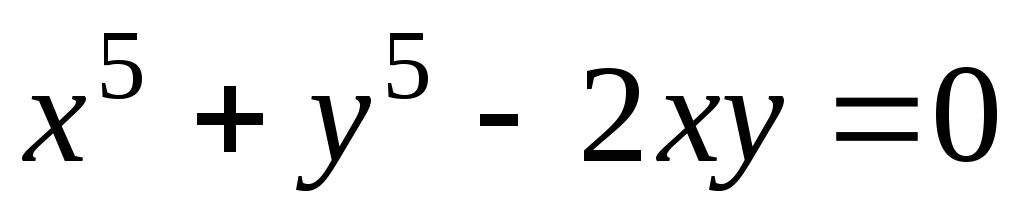 в точке
М(1,1).
в точке
М(1,1).Точка движется по логарифмической спирали
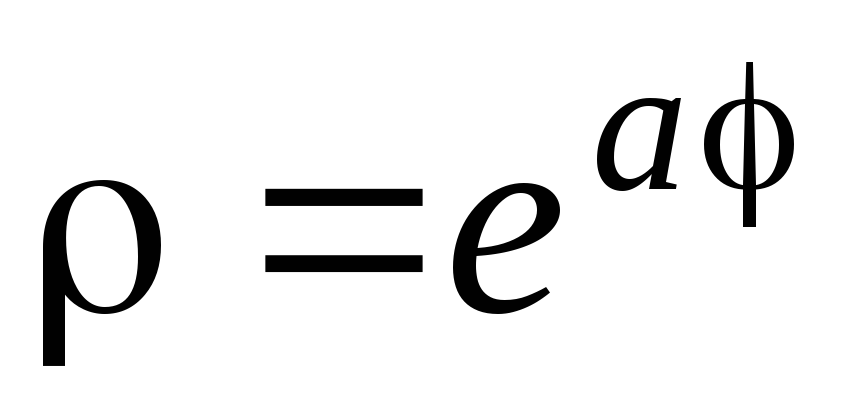 .
Найти скорость изменения полярного
радиуса
.
Найти скорость изменения полярного
радиуса ,
если известно, что он вращается с
постоянной скоростью
,
если известно, что он вращается с
постоянной скоростью .
.Доказать приближенную формулу
 .
.Вычислить, используя правило Лопиталя: а)
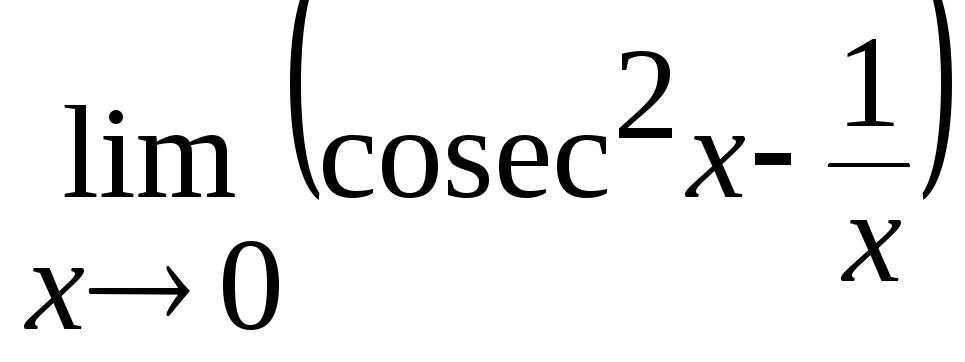 б)
б)

Найти асимптоты графика функции
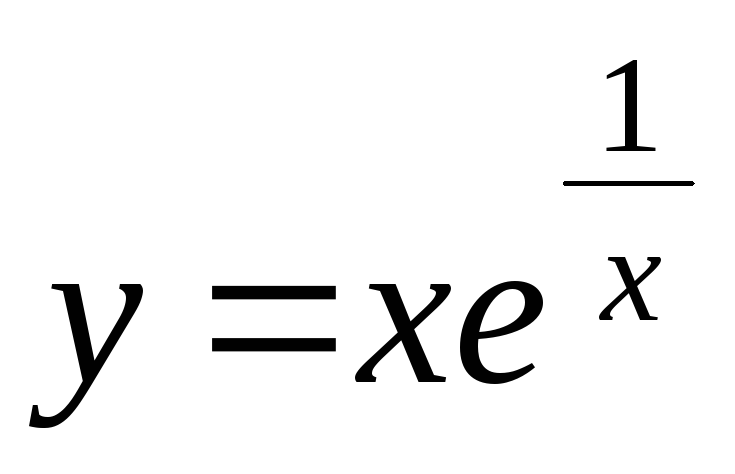
По графику функции описать ее свойства: четность, нечетность, непрерывность, характер точек разрыва, интервалы монотонности, экстремумы, интервалы выпуклости, вогнутости, точки перегиба, уравнения асимптот.

Исследовать функцию и построить ее график:
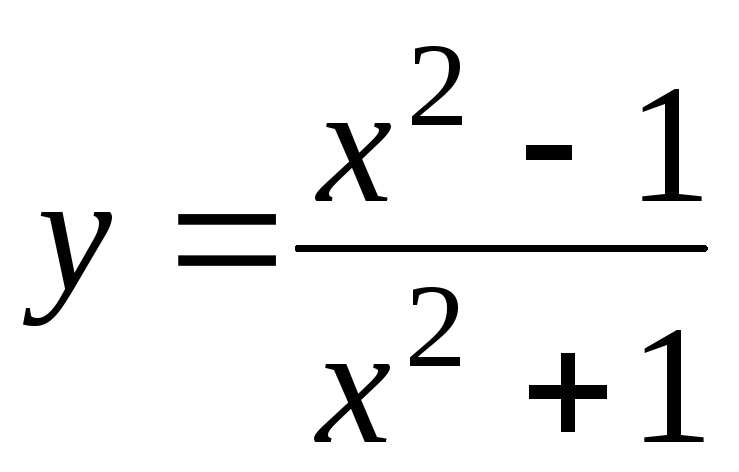 .
.Найти наибольшее и наименьшее значения функции
 на [
на [ ].
].Прямой круговой конус описан около прямого кругового цилиндра так, что плоскости и центры их оснований совпадают. Радиус основания цилиндра равен 4, а высота равна 6 .Найти радиус основания и высоту конуса, при которых его объем будет наименьшим.
Вариант 3
В какой точке касательная к параболе
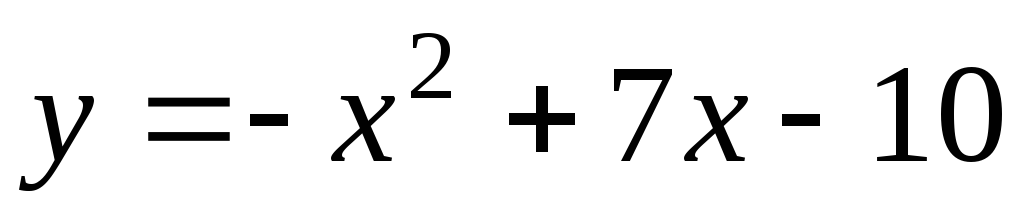 перпендикулярна прямой
перпендикулярна прямой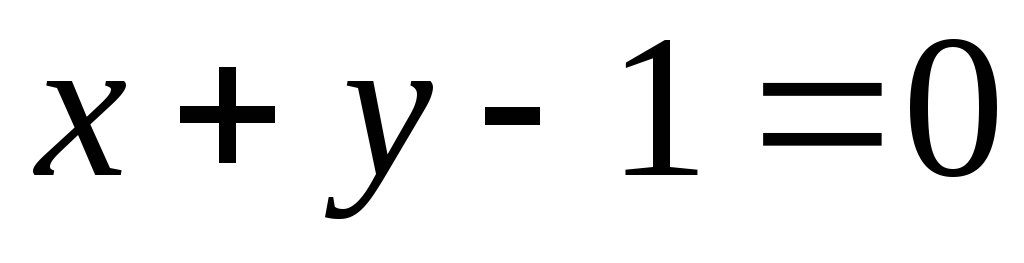 .
Составить уравнение касательной.
.
Составить уравнение касательной.Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за время Т = 8 сек. Найти угловую скорость w в момент t = 32 сек после начала движения.
На сколько приближенно изменится значение степени 25, если основание увеличить на 0,003?
Вычислить, используя правило Лопиталя: а)
 б)
б)

Найти асимптоты графика функции
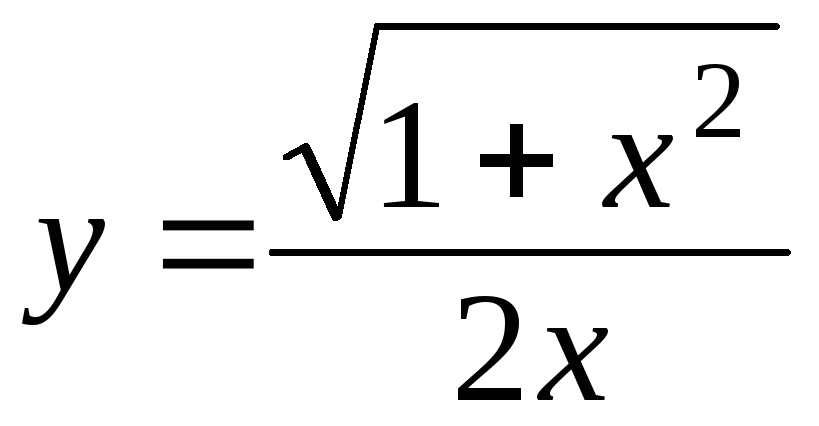 .
.По графику функции описать ее свойства: четность, нечетность, непрерывность, характер точек разрыва, интервалы монотонности, экстремумы, интервалы выпуклости, вогнутости, точки перегиба, уравнения асимптот.

Исследовать функцию и построить ее график:
 .
.Найти наибольшее и наименьшее значение
 на отрезке [-3;1]
на отрезке [-3;1]Прямой круговой конус описан около полушара так, что центр основания конуса совпадает с центром шара. Радиус шара равен 5. Найти радиус основания и высоту конуса, при которых его объем будет наименьшим.
