
Из «Аналитическая геометрия»
|
Номер варианта |
Номер задания (и часть 1, и часть 2) |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
N N=1–10 |
N |
N |
N |
N |
N |
N |
N |
N |
N |
|
Например, для варианта 8 все задания берутся под номером 8 |
|||||||||
|
11 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
12 |
1 |
3 |
5 |
7 |
9 |
2 |
4 |
6 |
8 |
|
13 |
3 |
4 |
6 |
8 |
10 |
1 |
2 |
5 |
7 |
|
14 |
4 |
5 |
2 |
9 |
6 |
3 |
7 |
1 |
10 |
|
15 |
5 |
8 |
3 |
1 |
4 |
10 |
7 |
2 |
6 |
|
16 |
6 |
7 |
1 |
10 |
2 |
9 |
8 |
3 |
5 |
|
17 |
7 |
9 |
10 |
2 |
1 |
8 |
3 |
5 |
6 |
|
18 |
8 |
6 |
5 |
3 |
9 |
7 |
2 |
10 |
1 |
|
19 |
9 |
10 |
4 |
7 |
5 |
6 |
3 |
1 |
2 |
|
20 |
10 |
2 |
2 |
4 |
3 |
5 |
8 |
6 |
7 |
|
21 |
3 |
4 |
10 |
6 |
1 |
2 |
8 |
7 |
5 |
|
22 |
5 |
3 |
7 |
1 |
9 |
10 |
6 |
8 |
2 |
|
23 |
7 |
6 |
3 |
2 |
8 |
1 |
5 |
10 |
4 |
|
24 |
9 |
5 |
6 |
4 |
7 |
1 |
10 |
2 |
3 |
|
25 |
10 |
9 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
|
26 |
2 |
1 |
5 |
3 |
10 |
6 |
4 |
8 |
7 |
|
27 |
4 |
7 |
1 |
6 |
2 |
8 |
3 |
10 |
9 |
|
28 |
6 |
3 |
7 |
5 |
9 |
10 |
8 |
1 |
2 |
|
29 |
8 |
8 |
2 |
1 |
7 |
10 |
6 |
5 |
3 |
|
30 |
1 |
3 |
5 |
10 |
9 |
2 |
4 |
7 |
8 |
Часть 1
Задание 1
Построить прямые. Для прямой а) записать уравнение с угловым коэффициентом и уравнение в отрезках, для прямой е) – каноническое и общее:
1. а) 3x + 5y
– 10 = 0; б)
![]() в) –4y + 1 =0;
г) x + 5
= 0; д)
в) –4y + 1 =0;
г) x + 5
= 0; д)
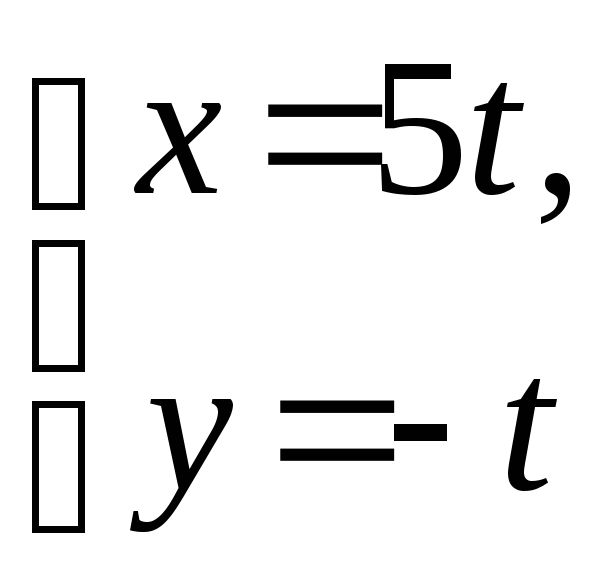 ;
е)
;
е)
 ;
ж)
;
ж)
![]()
2.
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]() ; д)
; д)
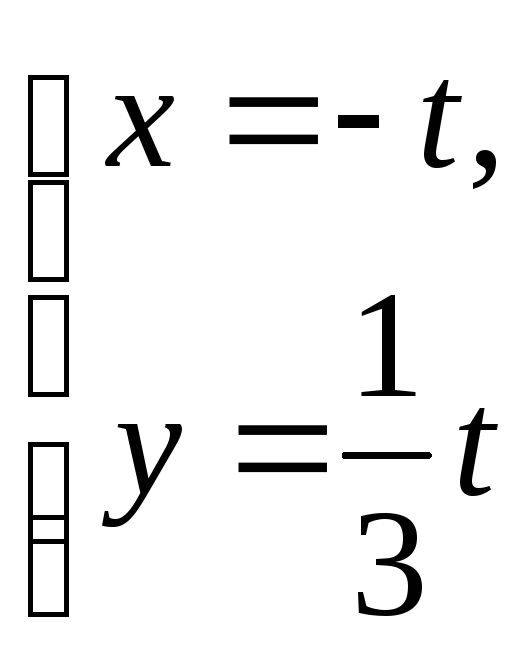 ;
е)
;
е)
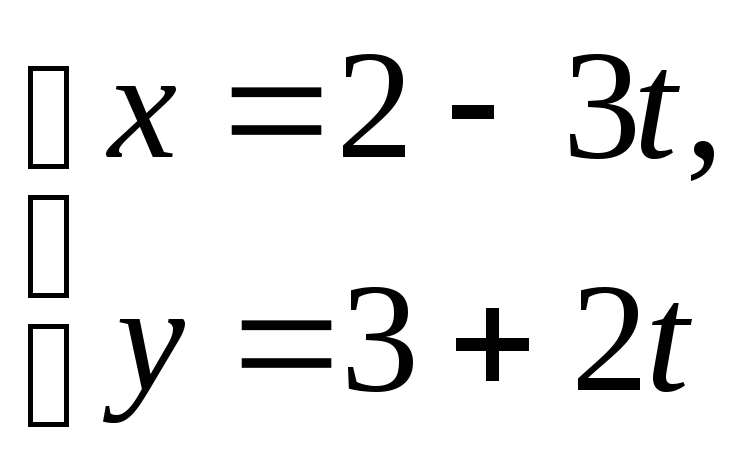 ;
ж)
;
ж)
![]() .
.
3.
а) 4x
+ 5y
– 12 = 0; б)
![]() ;
в) –4y
+ 1 =0;
г) x
+ 5 = 0; д)
;
в) –4y
+ 1 =0;
г) x
+ 5 = 0; д)
 ;
е)
;
е)
 ;
ж)
;
ж)
![]()
4. а)
–2x + 3y – 8 = 0; б)
![]() ;
в) –3y + 4 = 0;
г) х
+ 5 = 0; д)
;
в) –3y + 4 = 0;
г) х
+ 5 = 0; д)
 е)
е)
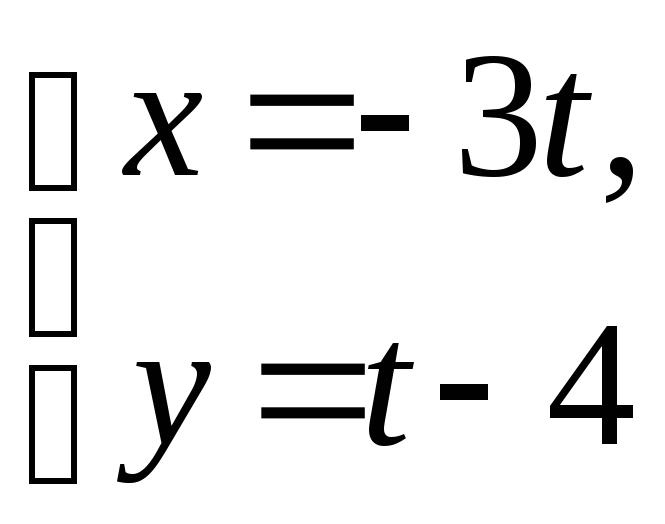 ;
ж) 4x
= 0.
;
ж) 4x
= 0.
5. а) x + 5y + 4 = 0; б) x + 7y = 0; в) 3x - 10 = 0;
г)
4y
+ 5 = 0; д)
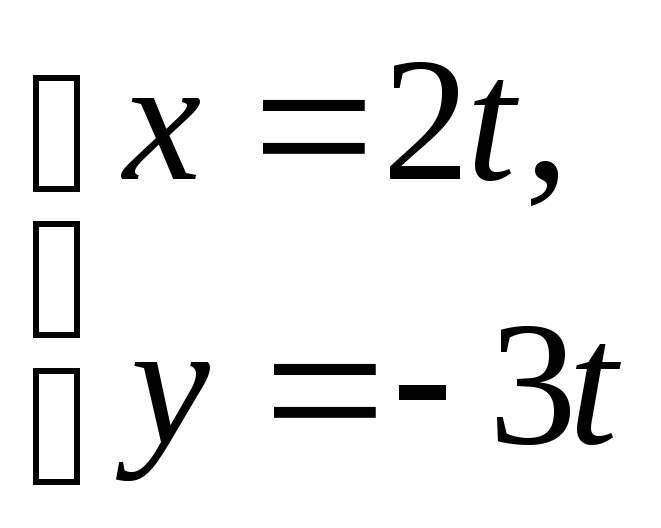 ;
е)
;
е)
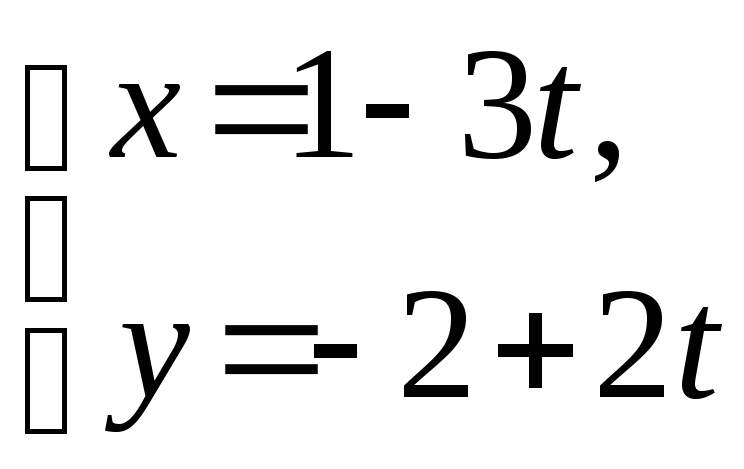 ;
ж) 11y
= 0.
;
ж) 11y
= 0.
6. а) 2x + y – 3 = 0; б) 2x – 5y = 0; в) 3x + 1 = 0;
г)
4y
– 3 = 0; д)
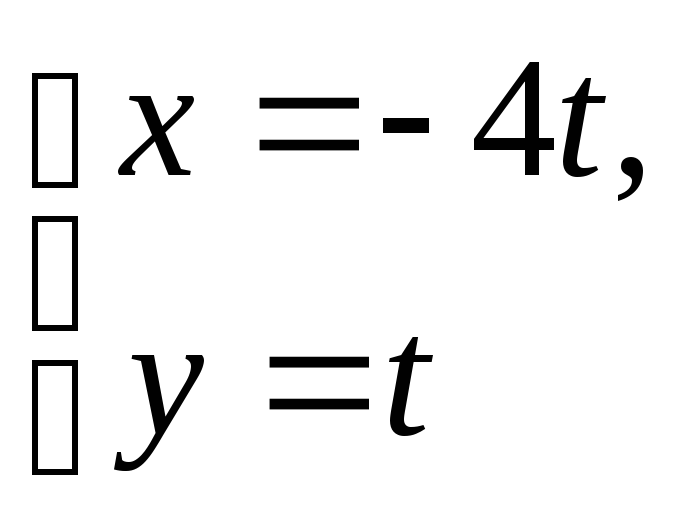 ;
е)
;
е)
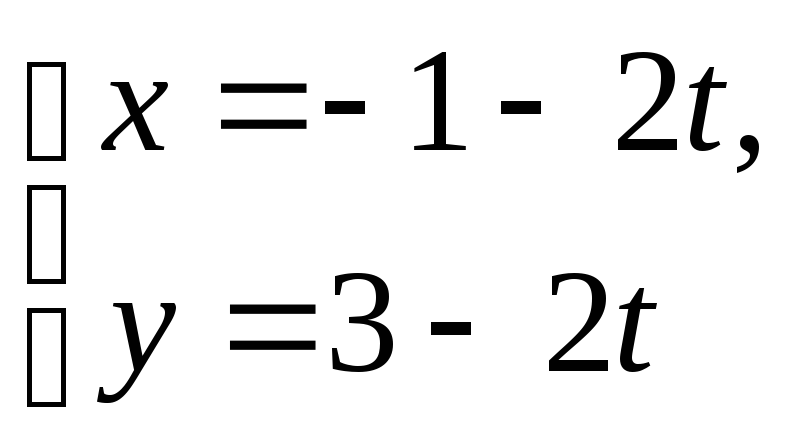 ,
ж) 11х
= 0.
,
ж) 11х
= 0.
7.
а) 2x
+ 4y
+1 = 0; б) 3y
+ 2x
= 0; в) –2x
+ 3 = 0;
г) y
+ 1 = 0; д)
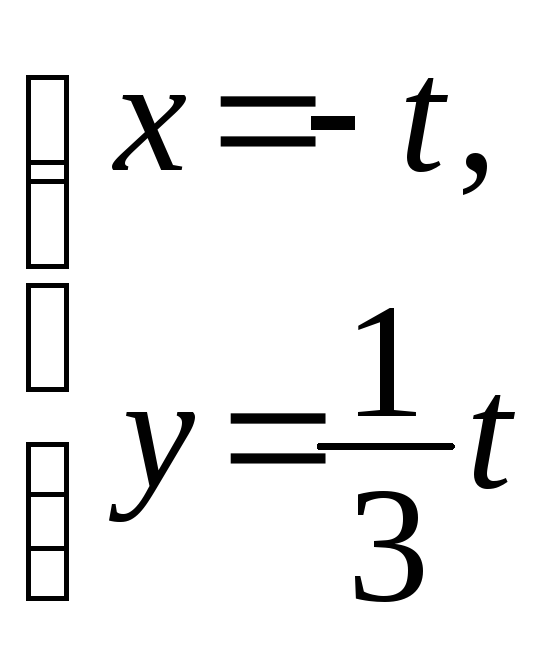 ; е)
; е)
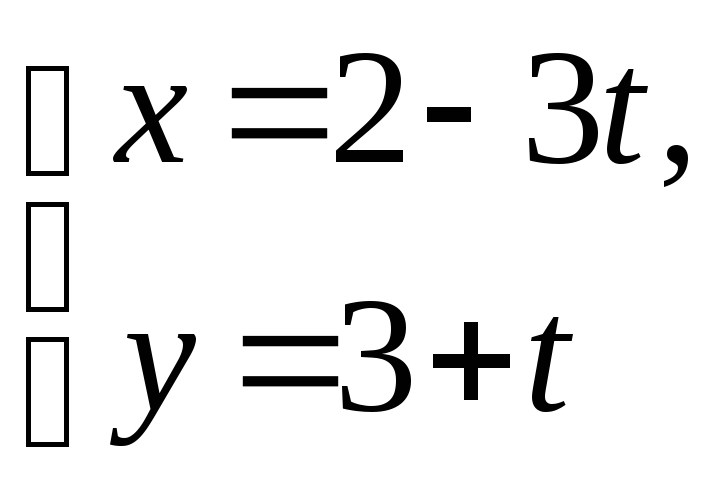 ; ж)
0.5y
= 0.
; ж)
0.5y
= 0.
8.
а) 4x
– 3y
+ 9 = 0; б)
![]() ; в)
3x
– 2 = 0;
г) y
+ 5 = 0; д)
; в)
3x
– 2 = 0;
г) y
+ 5 = 0; д)
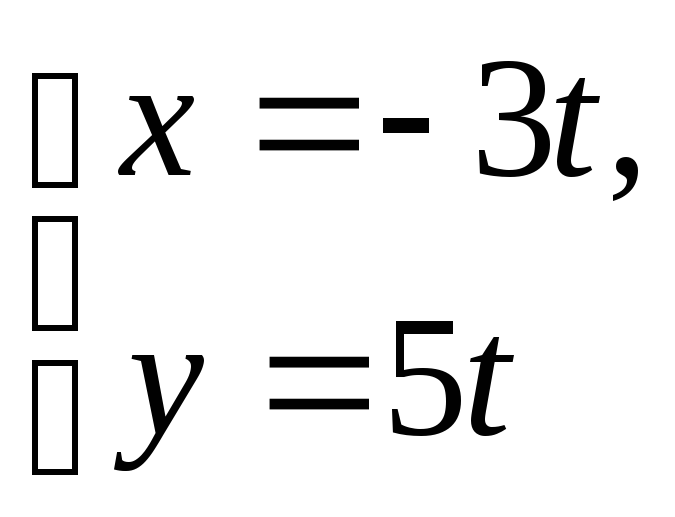 ;
е)
;
е)
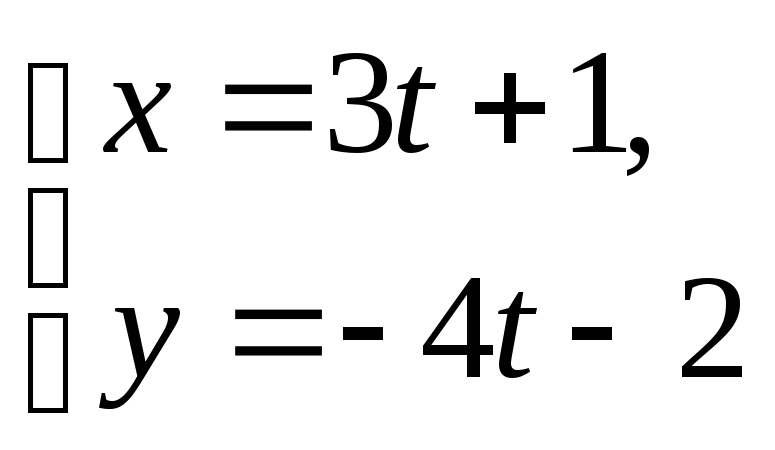 ; ж)
; ж)
![]() .
.
9.
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
 ;
е)
;
е)
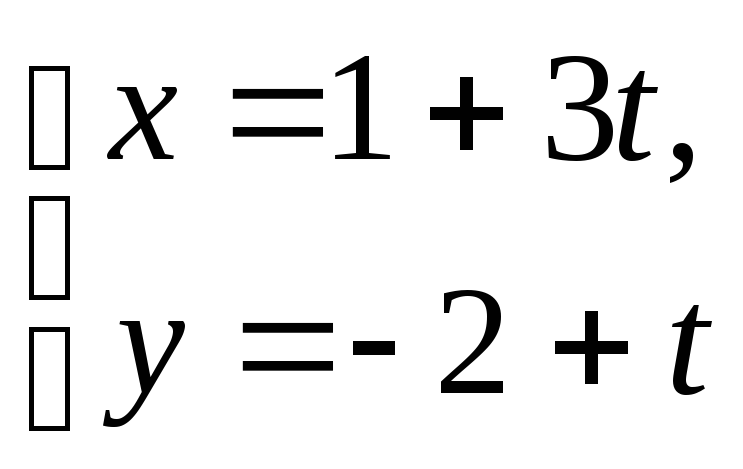 ;
ж)
;
ж)
![]() .
.
10.
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]() ; д)
; д)
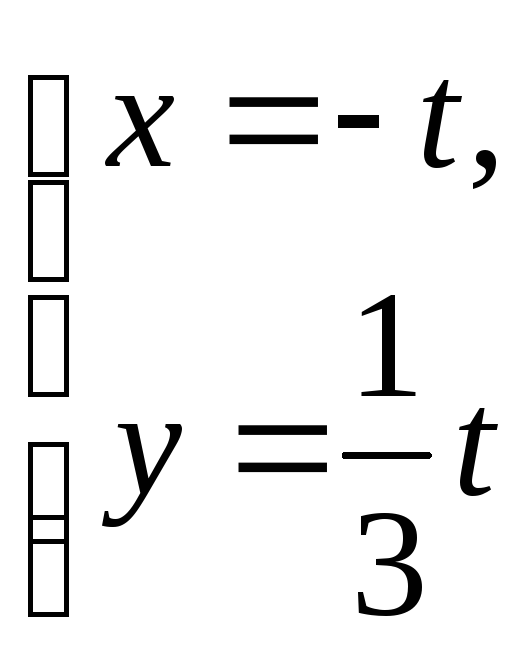 ; е)
; е)
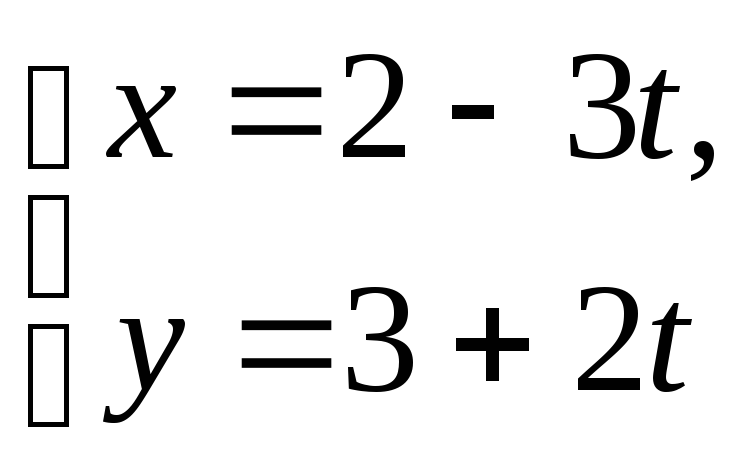 ; ж)
; ж)
![]() .
.
Задание 2.
Даны вершины А, В, С треугольника. Найти:
а) уравнения сторон;
б) угол C;
в) уравнение и длину высоты, опущенной из вершины А;
г) уравнение медианы, проведенной из точки В.
д) уравнения сторон параллелограмма ABCD и координаты вершины D.
-
А(1,-2), В(4,0), С(-2,3)
-
А(1,2), В(-3,0), С(2,2)
-
А(0,-3), В(2,4), С(5,-6)
-
А(1,-1), В(3,0), С(-2,3)
-
А(1,-2), В(3,2), С(0,-1).
-
А(-2,1), В(0,1), С(-4,3)
-
А(2, -1), В(0,2), С(4,-3)
-
А(-1,1), В(-2,3), С(2,2)
-
А(1, -2), В(3,1), С(2,2)
-
А(1,-3), В(0,4), С(5,-6)
Задание 3.
Построить плоскости:
1. а) 2x – y – 3z + 8 = 0; б) 2x – z – 4 = 0; в) 3x + 5 = 0; г) – 7z = 0 .
-
а)
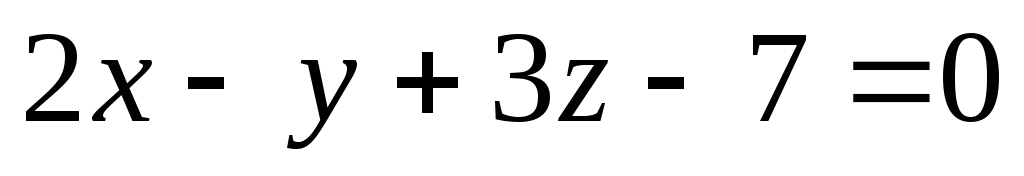 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
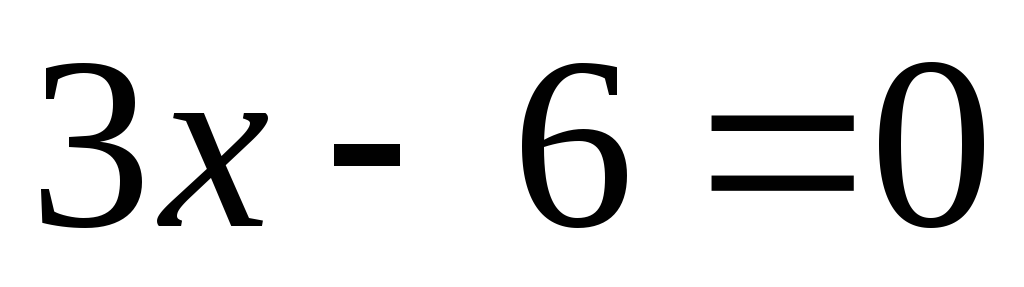 ;
д)
;
д)
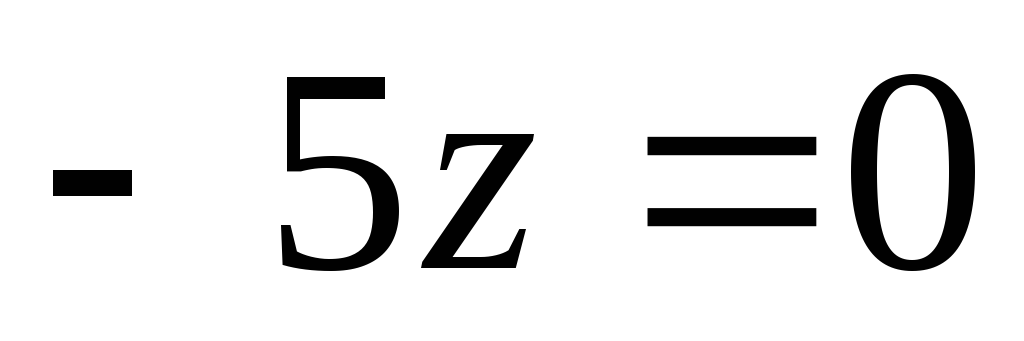 .
. -
а) –x + y – 7z + 9 = 0; б) 3x + z + 6 = 0; в) 2y + z = 0; г) 5x + 10 = 0; д)
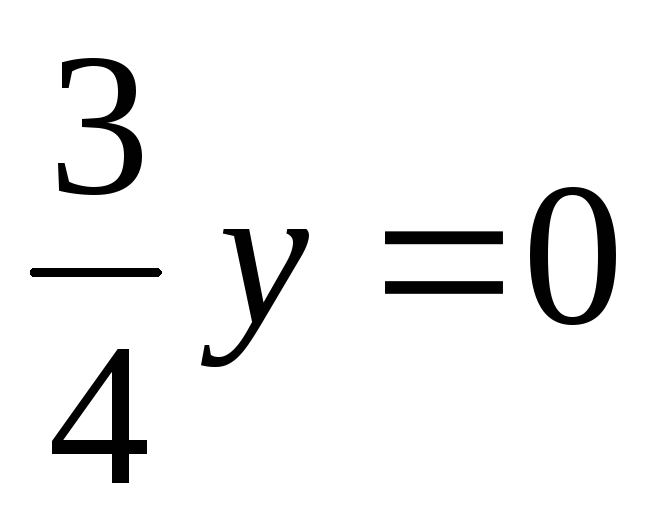
-
а) –3x + y – 2z + 8 = 0; б) 2x – 4z + 8 = 0; в) 2х + z = 0; г) 5x + 8 = 0; д)
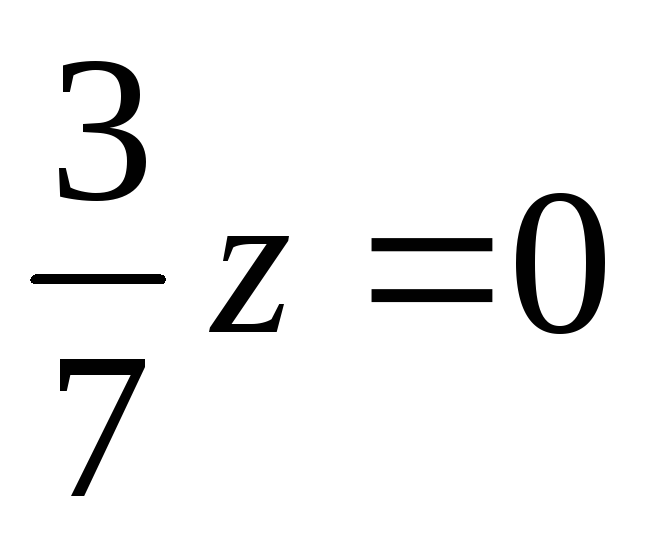 .
. -
а) 2x – y – 3z + 8 = 0; б) 2x – z – 4 = 0; в) 3у – z = 0;г) 3x + 5 = 0, д) – 7z = 0 .
-
а) –3x + y + 2z + 9 = 0; б) 2y + z – 5 = 0; в) x – 3y = 0; г) 4z + 6 = 0; д)
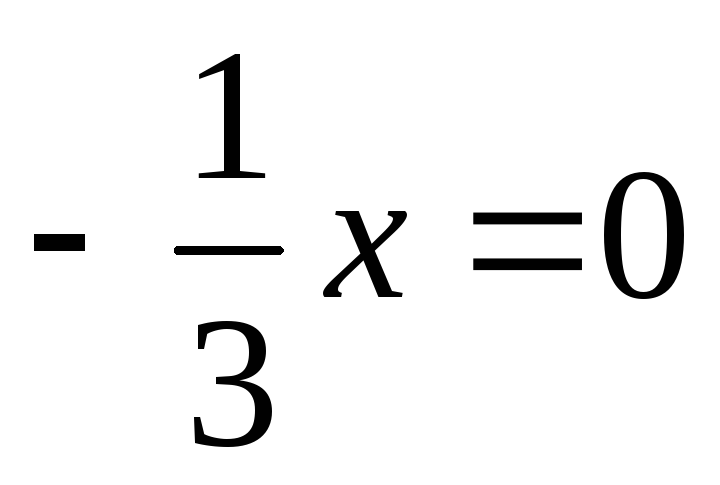 .
. -
а)
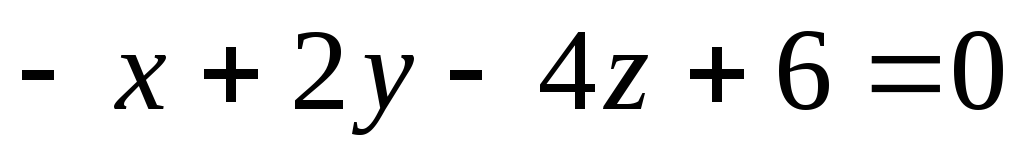 ;
б)
;
б)
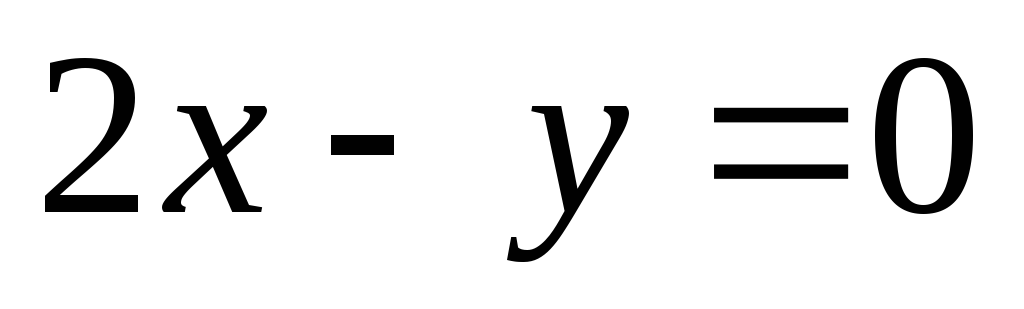 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д) .
. -
а) 3x – 2y – 3z + 10 = 0; б) –2x + y = 4; в) 3y – z = 0; г) 5z – 8 = 0; д)
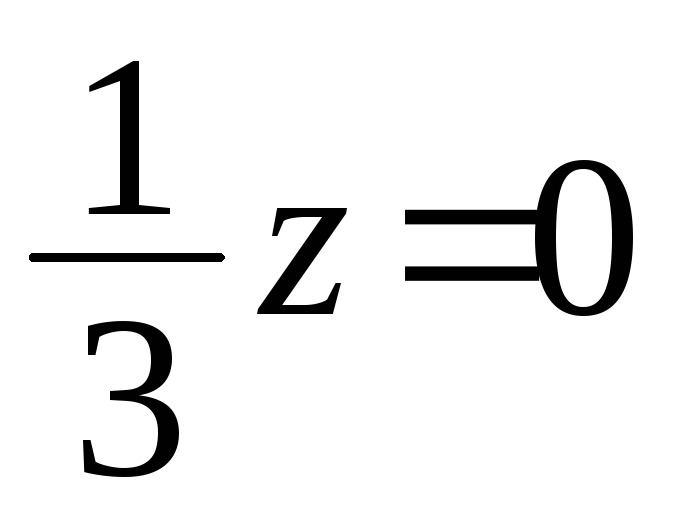
-
а) –x + y – 7z + 9 = 0; б) 3x + z + 6 = 0; в) 2y + z = 0; г) 5x + 10 = 0; д)
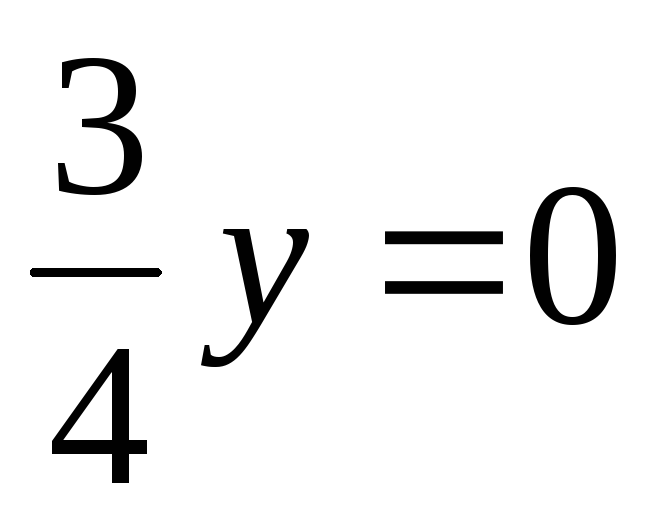 .
. -
а) –3x + y – 2z + 8 = 0; б) 2x – 4z + 8 = 0; в) 3x – 2y = 0; г) 5x + 8 = 0; ж)
 .
.
Задание 4
Найти проекцию точки А на плоскость, проходящую через точки М1, М2, М3. Найти расстояние от точки А до этой плоскости. Сделать чертеж.
-
А(-2,1,2), М1(-2,0,1), М2(0,2,-3), М3(1,2,-2).
-
А(-2,1,2), М1(1,0,2), М2(1,1,1), М3(-3,-2,1)
-
А(-1,1,2), М1(2,1,0), М2(1,0,-1), М3(2,-1,-1).
-
А(-2,1,1), М1(1,-1,1), М2(2,1,-1), М3(0,3,2).
-
А(0,1,-2), М1(-2,1,0), М2(0,-3,2), М3(1,-2,2).
-
А(-2,1,2), М1(-2,0,1), М2(0,2,-3), М3(1,2,-2).
-
А(-2,1,2), М1(1,0,2), М2(1,1,1), М3(-3,-2,1)
-
А(-1,-1,1), М1(1,0,2), М2(2,1,-1), М3(0,2,-1).
-
А(-2,1,1), М1(1,-1,1), М2(2,1,-1), М3(0,3,2)
-
А(0,1,-2), М1(-2,1,0), М2(0,-3,2), М3(1,-2,2).
Задание 5.
При каких значениях k указанные прямые или плоскости пересекаются в одной точке? Найти координаты точки пересечения.
-
3 – y – 12 = 0, kx – y – 5 = 0, x – y + 2 = 0.
-
 ,
,
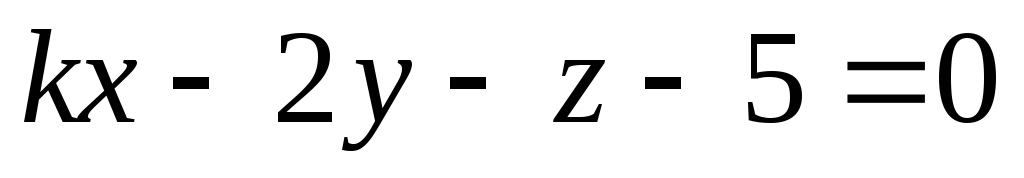 ,
,
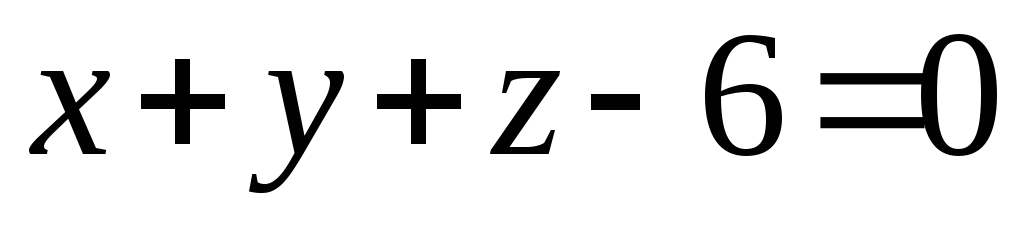 ,
,
 .
. -
y + 3x + 4 = 0, kx + y + 1 = 0, -x + 2y – 3 = 0.
-
2x – y + z = 0, kx + y + z = 6, 3x – 2y – z – 5 = 0, 4x – y – 11 = 0.
-
3 – y – 12 = 0, kx – y – 5 = 0, x – y + 2 = 0.
-
3x + y + 1 = 0, 4x + ky + 1 = 0, x + 2y = 0.
-
–x + 2y – 5 = 0, -x + y + 2 = 0, -x + ky – 12 = 0.
-
2x + 3y – z = 0, x + y + 3z – 5 = 0, 3x – 4y + kz = 0.
-
x – 2y – 4 = 0, x + y + 2 = 0,–-x + ky – 12 = 0.
-
2x – y + z = 0, kx + y + z = 6, 3x – 2y – z – 5 = 0, 4x – y – 11 = 0.
Задание 6.
Записать канонические уравнения прямой L. Составить уравнение плоскости, проходящей через L перпендикулярно плоскости .
-
L:
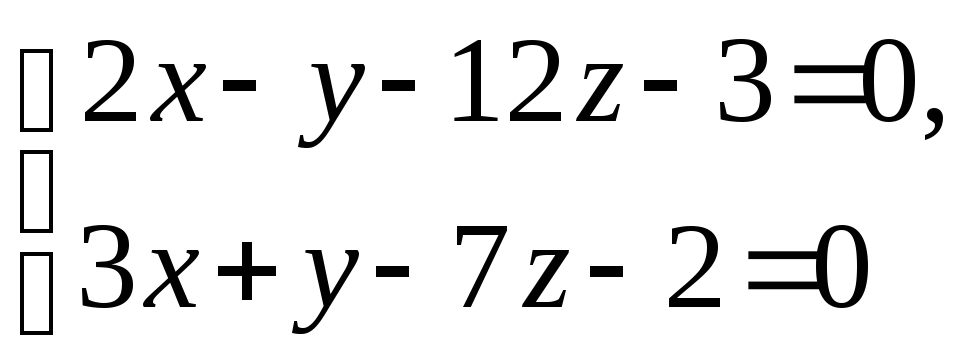 ,
:
,
:
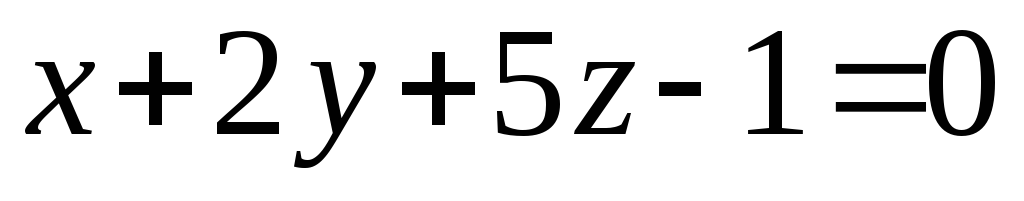
-
L:
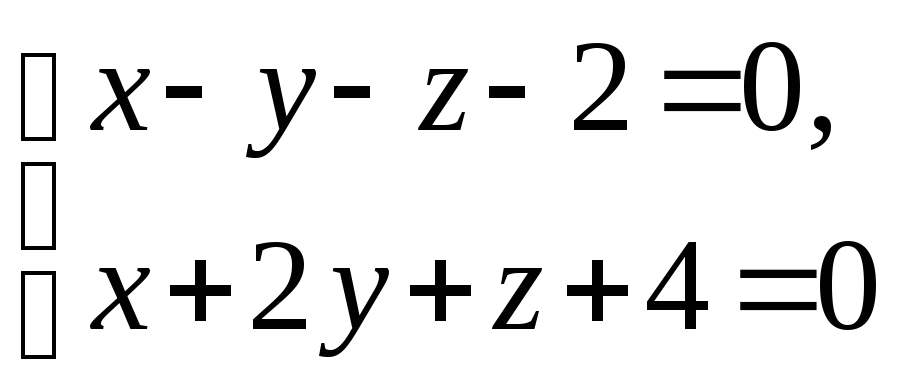 ,
:
,
:
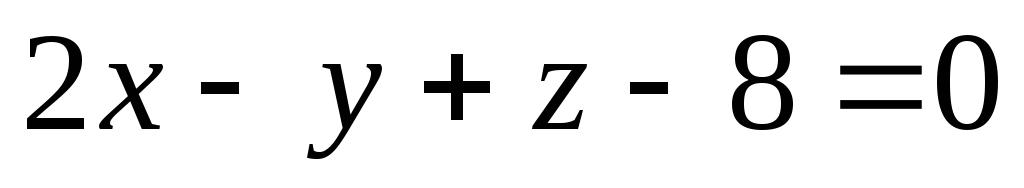
-
L:
 , :
, :
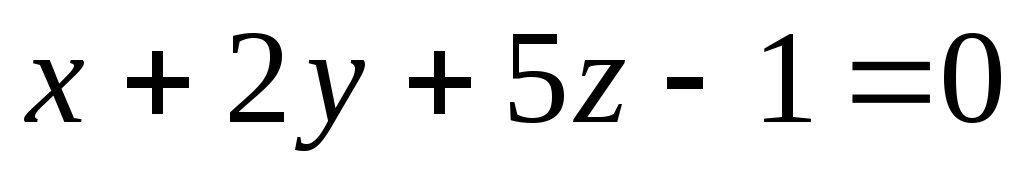 .
. -
L:
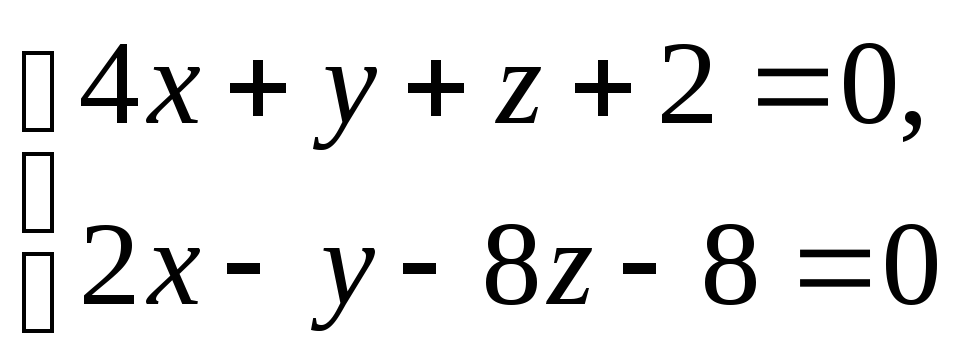 , : 5x + y
+ 2z + 4 = 0.
, : 5x + y
+ 2z + 4 = 0. -
L:
 , :
2x – y + z – 6 = 0
, :
2x – y + z – 6 = 0 -
L:
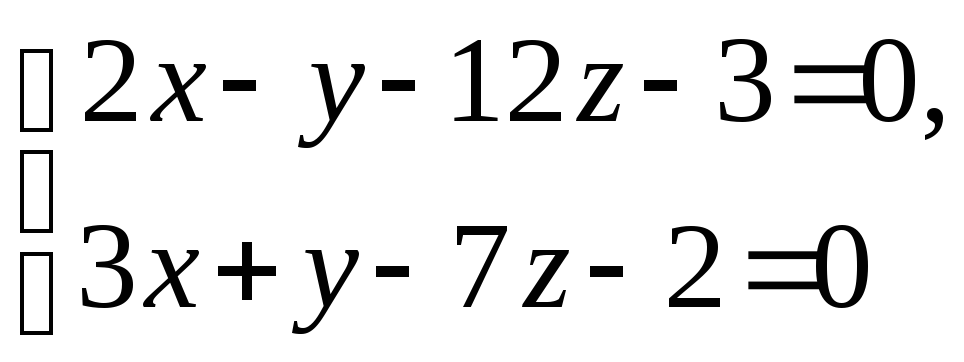 , :
, :

-
L:
 , : x
– 3y +
2z + 2 =
0.
, : x
– 3y +
2z + 2 =
0. -
L:
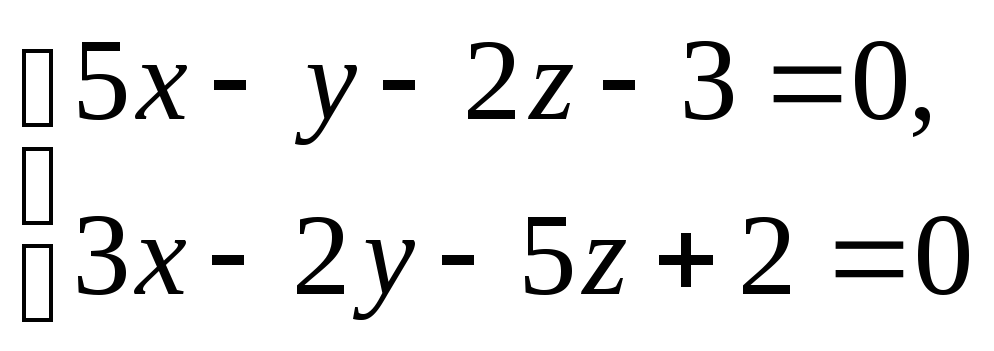 , : x + 19y
- z - 11 = 0
, : x + 19y
- z - 11 = 0 -
L:
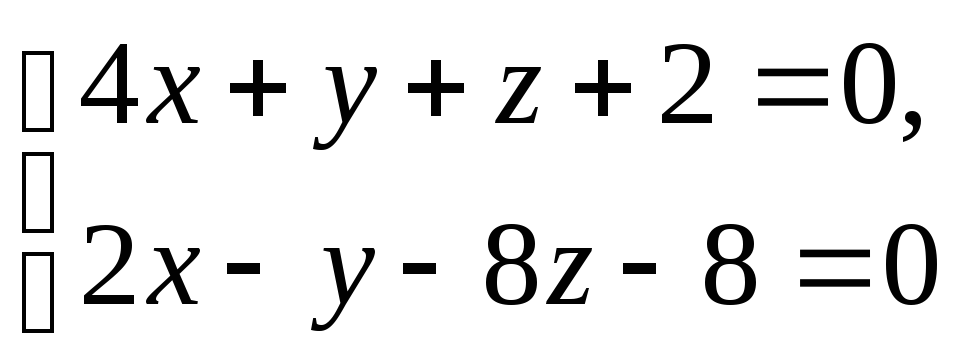 , : 5x
+ y
+ 2z
+ 4 = 0
, : 5x
+ y
+ 2z
+ 4 = 0 -
L:
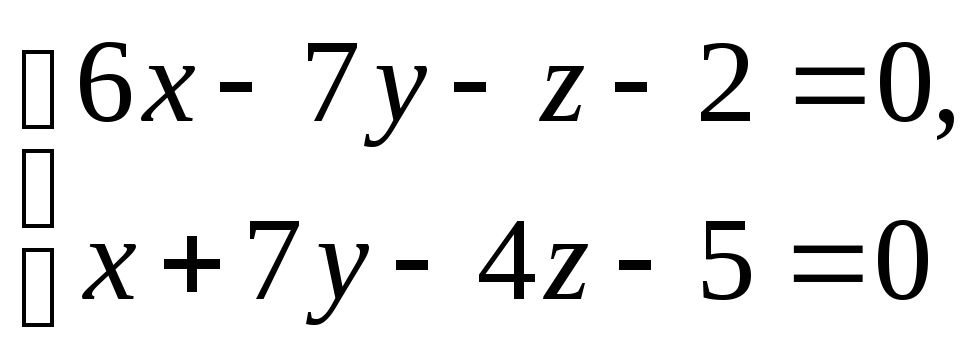 , : 2x
– y
+ z
– 6 = 0
, : 2x
– y
+ z
– 6 = 0
