2.2. Экономический смысл производной

Пусть - объем производимой продукции в зависимости от объемазатраченного ресурса. Относительное приращениеявляетсясредней производительностью ресурса. Производнаяназываетсяпредельным продуктом илипроизводительностьюресурса.

Она характеризует изменение выпуска продукции, вызванное увеличением затрат данного ресурса на 1 усл. ед.

Пример. Функция выпуска имеет вид , где- объем продукции,- время. Найти предельную производительность ресурса для затрат ресурса равных 3 усл. ед.

Решение

;

- это изменение выпуска продукции , вызванное увеличением затрат данного ресурсана 1 усл. ед. от величины.

3. Основные правила дифференцирования

Если - постоянная,и- дифференцируемые в точкефункции, то их алгебраическая суммапроизведениеи частноетакже дифференцируемы в этой точке, причем справедливы следующиеосновные правила дифференцирования:

1. ;

2. ; ;

3. Постоянный множитель выносится за знак производной: ;

4. ; где .

5. Производная сложной функции.Пусть- сложная функция, т.е. промежуточный аргумент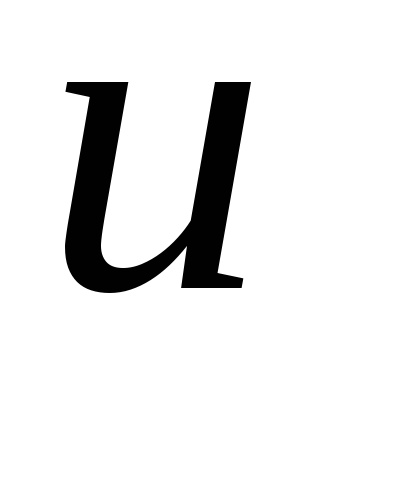является функцией от.

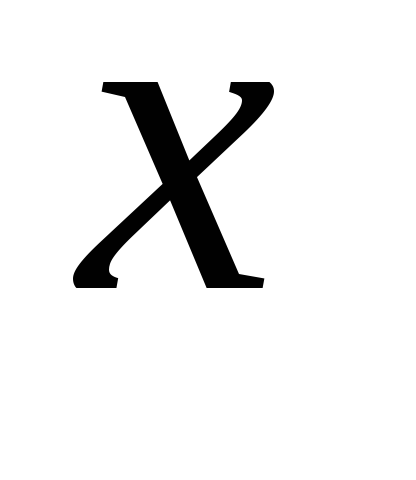Производная сложной функции равна произведению производной функции по промежуточному аргументуна производную от промежуточного аргумента по независимой переменной.

.

Пример. Найти производную функции.

Запишем , тогда- степенная функция,- тригонометрическая функция. Для сложной функциипроизводная равна.

4. Таблица основных формул дифференцирования

Элементарная функция - независимая переменная	Сложная функция - дифференцируемая функция
1. Постоянная функция
2. Степенная функция
3. Показательная функция
Экспонента	Экспонента
4. Логарифмическая функция
5. Тригонометрические функции
6. Обратные тригонометрические функции

5. Производные высших порядков

Для функции ее производнаятоже является функцией.

• Производной второго порядка называется производная от производной и обозначается,.

Если первая производная есть скорость некоторого процесса, то вторая производная характеризует ускорение того же процесса.

• Производной - ого порядка называется производная от производной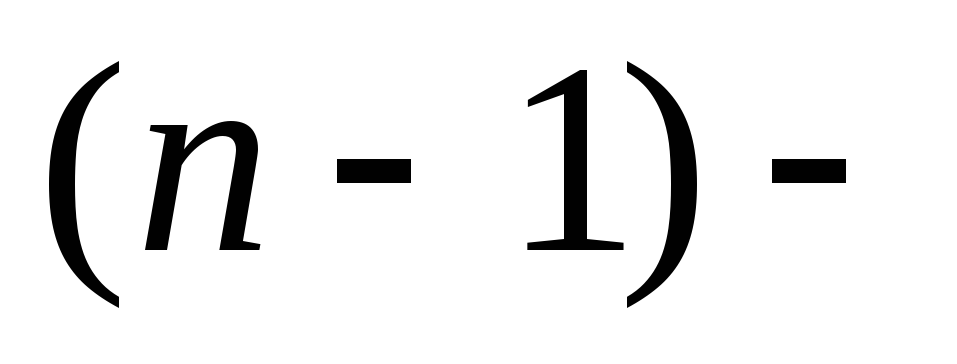го порядка:_.

Пример 1.

.

• Функция называется n раз дифференцируемой в точке , если в этой точке существуют все производные до n-го порядка включительно, т.е. _, ,, …,.

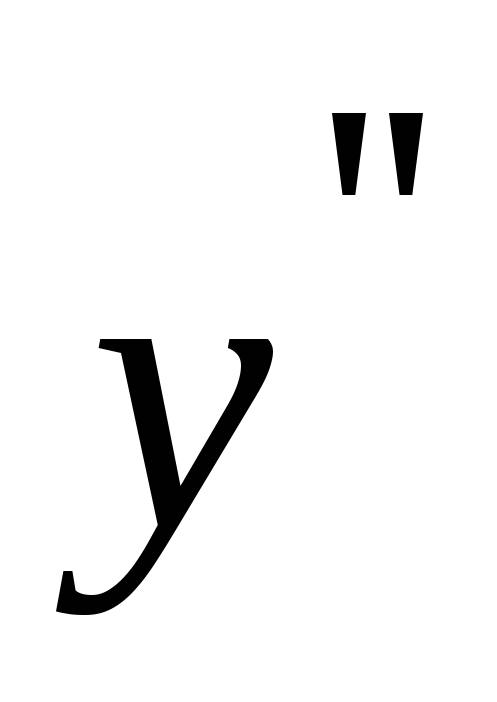Пример 2. Найти значение для функции.

Сначала найдем производную , а затем вычислим ее значение в точке.

; ;

; .

6. Вычисление пределов с помощью производных

Производные часто применяют для раскрытия неопределенностей вида или.

Правило Лопиталя

Пусть функции иимеют производные в окрестности точки, причем в точкезначение производной.

Если или, то предел отношения функций равен пределу отношения их производных:

.

Если предел отношения производных снова представляет собой неопределенность видаили, то применяют правило вторично.

Пример 3. Используя правило Лопиталя, найти пределы: