2. Основные свойства пределов

1. Если предел функции в точке существует, то он единственный.

2. Предел постоянной величины равен самой постоянной:

.

3. Предел суммы (разности) конечного числа функций равен соответственно сумме (разности) пределов этих функций:

.

4. Предел произведения конечного числа функций равен произведению пределов этих функций:

.

Следствие. Постоянный множитель можно выносить за знак предела:

.

4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю:

(при ).

Все свойства имеют смысл, если пределы функций существуют.

Для вычисления пределов используется свойство элементарных функций: если - элементарная функция, то . Это означает, что если предельная точкапринадлежит области определения функции, то вычисление пределасводитсяк подстановке в функцию вместо числа .

Пример. Вычислить предел .

Точка принадлежит области определения функции, значит,.

3. Бесконечно малые и бесконечно большие функции

При вычислении пределов большую роль играют бесконечно малые и бесконечно большие функции и их свойства.

• Функция называетсябесконечно малой функцией при (или при ), если она при этом стремится к нулю:.

Примеры.

1. Функция 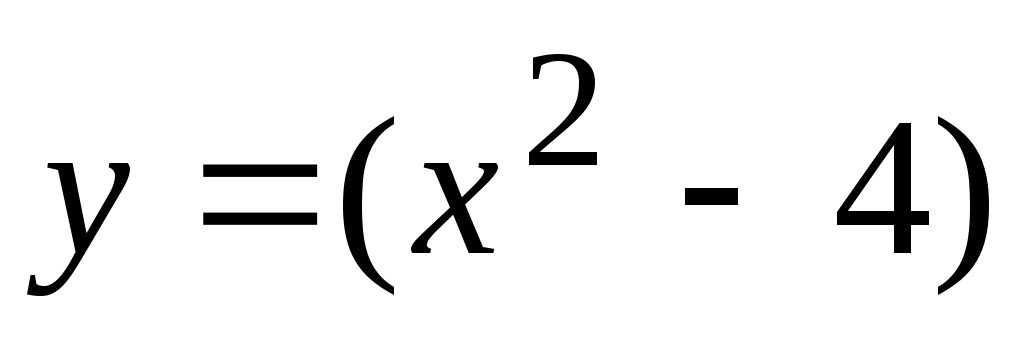- б.м.ф. в точках, т.к..

2. Функция - б.м.ф. при, т.к..

• Функция называетсябесконечно большой функцией при (при ), если ее предел равен бесконечности:.

Примеры.

3. Функция - б.б.ф. при, т.к..

4. Функция 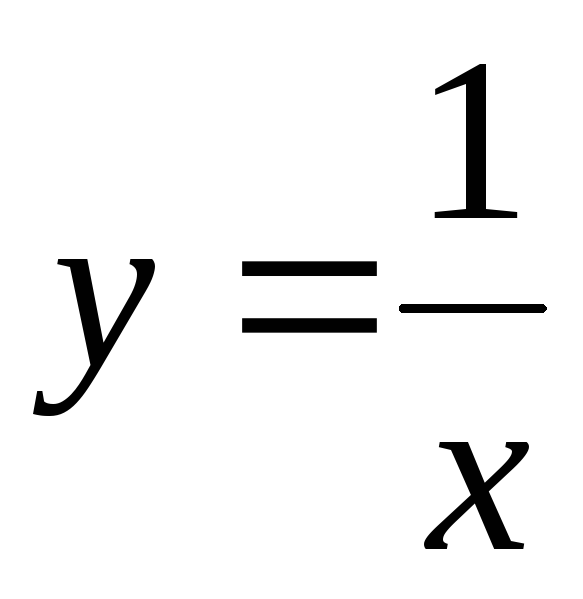- б.б.ф. в точке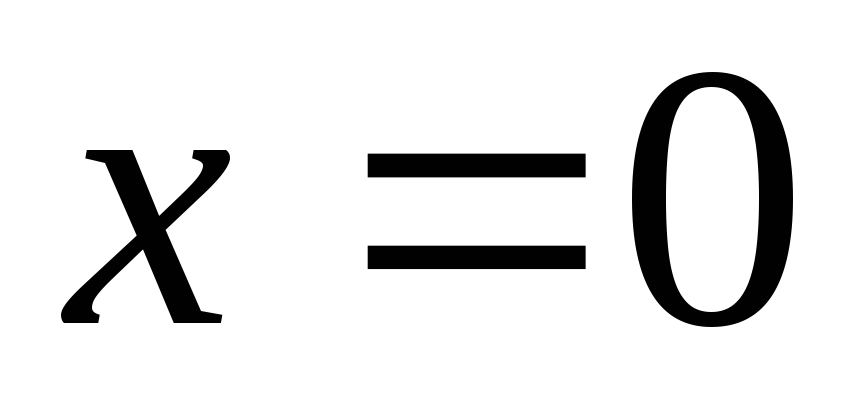, т.к..

Отметим важные свойства бесконечно малых и бесконечно больших функций.

Теорема (Свойства б.м.ф.)

1. Алгебраическая сумма конечного числа б.м.ф. и произведение конечного числа б.м.ф. есть бесконечно малая функция.

2. Произведение б.м.ф. на ограниченную функцию есть бесконечно малая функция.

3. Частное от деления б.м.ф. на функцию, имеющую в точке ненулевой предел, есть б.м.ф.

4. Функция, обратная к бесконечно малой, есть бесконечно большая функция:

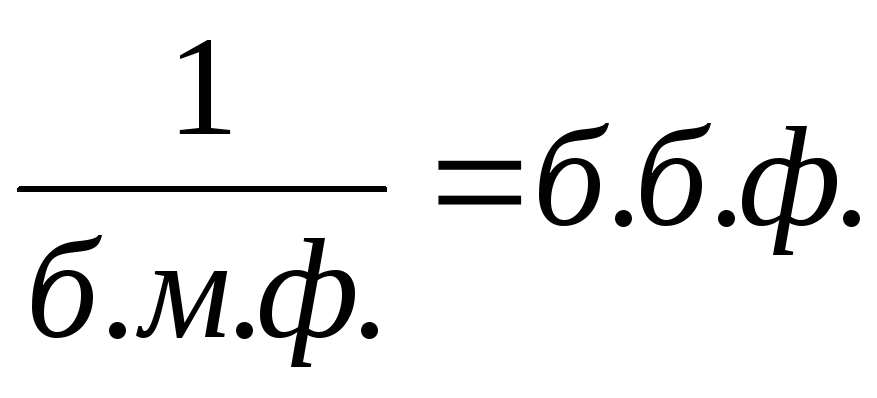
Теорема (Свойства б.б.ф.)

5. Произведение конечного числа б.б.ф. есть бесконечно большая функция.

6. Произведение б.б.ф. на функцию, имеющую предел, не равный нулю, есть бесконечно большая функция.

7. Функция, обратная к бесконечно большой, есть бесконечно малая функция:

Примеры. Вычислить пределы.

1. .

2..

3. .

4. Раскрытие неопределенностей ,

Часто подстановка предельного значения аргумента в функцию приводит к неопределенным выражениям вида ,,,и так далее. В таких ситуациях при вычислении предела нельзя применить равенство, ни свойства б.м.ф. и б.б.ф. Нахождение предела в таких случаях называется «раскрытием неопределенности».

Для раскрытия неопределенностей в пределе используют различные приемы.

Неопределенность вида . Если функция есть отношение многочленов, то для раскрытия неопределенности нужно числитель и знаменатель разделить почленно на в наибольшей степени.

Пример.

Запишем правило вычисления предела отношения двух многочленов при раскрытии неопределенности типа .

Неопределенность вида .

А) Если функция естьотношение многочленов , то для раскрытия неопределенности нужно разложить многочлены ина множители и сократить на множитель, стремящийся к нулю.

Б) Если функция содержит иррациональность, то для раскрытия неопределенности нужно избавиться от иррациональности с помощью формул сокращенного умножения и др.