8. Свойства функций, непрерывных на отрезке

• Функция называетсянепрерывной на отрезке 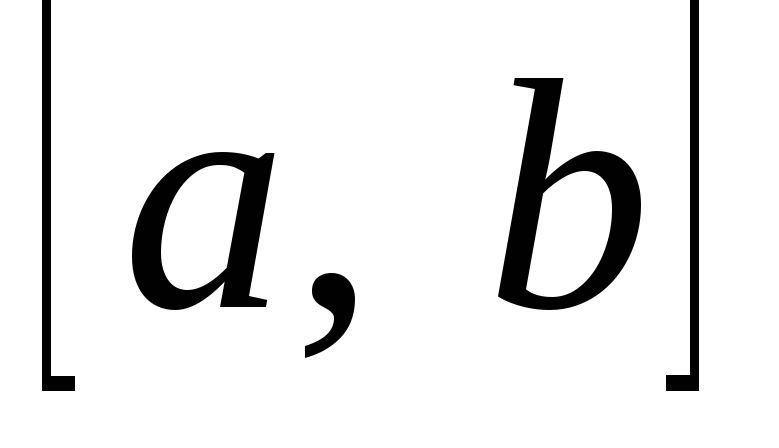, если она непрерывна в каждой точке этого отрезка.

Свойства функций, непрерывных на отрезке

1. Ограниченность непрерывной функции.

Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Это означает, что существует такое число , что для всех точекна отрезкевыполняется неравенство.

2. Существование наибольшего и наименьшего значений функции.

Если функция непрерывна на отрезке, то она достигает на этом отрезке как наименьшего, так и наибольшегосвоих значений.

То есть найдутся точки итакие, что

и .

3. Существование «нулей» функции.

Если функция непрерывна на отрезкеи на концах отрезка она принимает значения разных знаков (т.е.), то на отрезкенайдется хотя бы одна точка() такая, что значение функции в этой точке равно нулю. Такая точка, в которой, называетсянулем функции .

4. Существование промежуточных значений функции.

Если функция непрерывна на отрезке, то она принимает хотя бы по одному разу все промежуточные значения от наименьшегодо наибольшего.

То есть для любого числа , заключенного между числамии(), найдется точкатакая, что.

Контрольные вопросы

1. Сформулируйте определение предела функции при стремлении аргументак числу, предела функции при стремлении аргументак бесконечности.

2. Дайте определения предела функции при стремлении аргументак числусправа и слева.

3. Дайте определение предела функции y = f(x) при х  . Приведите аналитический и графический примеры.

4. Какая функция называется бесконечно малой? Приведите пример. Каковы свойства бесконечно малых функций?

5. Какая функция называется бесконечно большой? Приведите пример. Каковы свойства бесконечно больших функций?

6. Какая связь существует между бесконечно большими и бесконечно малыми функциями. Приведите примеры.

7. Сформулируйте основные теоремы о пределах функций.

8. Как раскрываются неопределенности вида , содержащие в числителе и знаменателе: 1) многочлены, 2) иррациональности?

9. Как раскрываются неопределенности вида , содержащие числителе и знаменателе многочлены?

10. Запишите первый замечательный предел.

11. Как раскрываются неопределенности вида , содержащие в числителе и знаменателе тригонометрические функции?

12. Запишите второй замечательный предел. Чему равно число ?

13. Как определяются натуральные логарифмы? Какова их связь с десятичными логарифмами?

14. Дайте определение непрерывной в точке х₀ функции. Сформулируйте необходимое и достаточное условие непрерывности функции в точке.

15. Сформулируйте правило исследования непрерывности функции в точке.

16. Сформулируйте свойства непрерывных функций.

17. Какая точка называется точкой разрыва функции? Какая точка называется точкой разрыва первого рода; точкой разрыва второго рода? Приведите графические примеры.

18. Если х₀ - точка разрыва функции, то означает ли это, что х₀ не принадлежит области определения этой функции?

19. Сформулируйте основные теоремы о функциях, непрерывных в точке.

20. Дайте определение функции , непрерывной на отрезке. Укажите области непрерывности основных элементарных функций.

21. Сформулируйте теоремы о функциях , непрерывных на отрезке.