5. Преобразования графиков функций

Построение графиков функций вида ипроизводится в несколько этапов, используя последовательно преобразования графиков.

Правило 1. Сдвиг (перенос) на данный отрезок вдоль оси абсцисс.

Чтобы построить график функции , нужно график функциисдвинуть вдоль осинаединиц вправо (при) и наединиц влево (при).

Правило 2. Сдвиг (перенос) на данный отрезок вдоль оси ординат.

Чтобы построить график функции , нужно график функциисдвинуть вдоль осинаединиц вверх (при) и наединиц вниз (при).

Правило 3. Растяжение (или сжатие) в данном отношении вдоль оси абсцисс.

График функции получается их графика функциисжатием вдоль осивраз (при), или растяжением враз (при).

Правило 4. Растяжение (или сжатие) в данном отношении вдоль оси ординат.

График функции получается их графика функциирастяжением вдоль осивраз (при), или сжатием враз (при).

Правило 5. Зеркальное отображение относительно оси абсцисс

Чтобы построить график функции , нужно оставить без изменения те участки графика функции, где, и зеркально отобразить относительно осиучастки графика, где.

Пример 9. Построить график функции с помощью преобразований графика функции.

Решение.

Выполним последовательные преобразования графика функции , который представляет собой прямую, проходящую через начало координат под угломк оси абсцисс.

Так как , то следует сдвинуть прямуюна 1 единицу вверх по оси(правило 2). Теперь строим график функции, зеркально отражая нижнюю часть графикаотносительно оси(правило 5). Построить график функции- значит, сдвинуть графикна 2 ед. вверх (правило 2).

Пример 10. Построить график функции .

Решение

Воспользуемся определением абсолютной величины числа.

; ;

; .

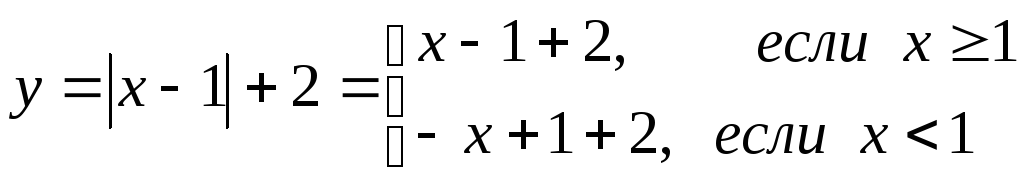На промежутке построим прямую, а на промежутке- прямую. Для каждой прямой зададим по две точки.

	- 1	0			1	2
	4	3			2	3

3

-1 0 1 2

График функции

Контрольные вопросы

1. Сформулируйте определение функции. В чем заключается однозначность функции?

2. Что называется областью определения и областью значений функции?

3. Какие существуют способы задания функции? Приведите примеры.

4. Дайте понятие графика функции . Может ли прямая а); б)пересекать график функциив нескольких точках?

5. Какая функция называется четной, нечетной? Приведите примеры.

6. Можно ли говорить о четности или нечетности функции, если область ее определения есть отрезок ?

7. Какая функция называется возрастающей, убывающей? Приведите графические примеры.

8. Опишите правила построения графиков функции вида и.

Тема 2. Предел и непрерывность функции одной переменной

Содержание

1. Предел функции в точке и на бесконечности.

2. Основные свойства пределов.

3. Бесконечно малые и бесконечно большие функции.

4. Раскрытие неопределенностей ,.

5. Первый и второй замечательные пределы

6. Эквивалентные бесконечно малые функции

7. Непрерывность функции, точки разрыва

8. Свойства функций, непрерывных на отрезке и в замкнутой области.