А) ; б).

а) Имеем неопределенность . Используем правило Лопиталя:

.

б) Имеем неопределенность . Представим произведение функций как отношение:

.

7. Дифференциал функции

Понятие дифференциала тесно связано с понятием производной и является одним из важнейших понятий в математике.

Пусть - функция, дифференцируемая в каждой точкеотрезка.

Производная этой функции определяется равенством .

Отношение пристремится к числуи, значит, отличается от производнойна бесконечно малую величину:, гдепри.

Умножая все члены последнего равенства на , получим. Произведениеесть бесконечно малая величина первого порядка относительно, так как.

Таким образом, приращение функции состоит из двух слагаемых, из которых первое слагаемое есть (при)главная частьприращения, прямо пропорциональная первой степени приращения, т.е.линейнаячасть относительно.

Пример 4.Найдем для функцииприращение функции:

Выделим в приращении функции ту часть, которая линейнаяотносительноприращения аргумента, это. Полученное выражение и будет называтьсядифференциалом функции:.

• Дифференциалом функции называетсяглавная, линейнаяотносительно приращения аргументачасть приращенияфункции.

В предыдущем примере . Заметим, что множитель- это производная функции:. Поэтому дифференциал функции равен произведению производнойна приращениеаргумента:

.

Подставим в эту формулу . Тогда, то есть

- дифференциал независимой переменной равен ее приращению .

Поэтому формула дифференциала функции примет вид

.

Эта формула показывает, что для нахождения дифференциала функции достаточно найти ее производную и умножить на .

Отсюда следует, что - производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

Пример 5. Найти дифференциал функции.

Решение..

Пример 6.Найти дифференциал функции .

Решение.

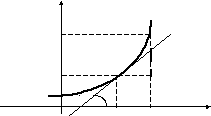
Геометрический смысл дифференциала функции

y

касательная

А

М В

Касательная в точке М разбивает отрезок ВNна два отрезка, один из которых АВ – этолинейная (главная) часть приращения функции, которая называетсядифференциалом и обозначается.

Из треугольника АВМ получим или. Таким образом, геометрическидифференциал функции в точке, равен приращению ординаты точки, движущейся по касательной к кривой.

8. Свойства дифференциала функции

Правила вычисления дифференциала следуют из его определения. Дифференциал функции обладает свойствами, аналогичным свойствам производной.

1) , 2),

3) , 4),

5) .

6) Дифференциал сложной функции имеет тот же вид, какой он имеет для независимой переменной (инвариантность формы дифференциала).

Пример 7. Дана функция . Найти.

Решение.

Представив данную функцию как сложную ,, находим дифференциал.

Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность дифференциала) позволит в дальнейшем ввести операцию, обратную дифференцированию (интегрирование).

9. Применение дифференциала к приближенным вычислениям

9.1. Приближенное вычисление значения функции в точке

Нужно вычислить значение функции в точке. Функцияможет быть задана в виде сложной формулы. Поэтому довольно часто прибегают к приближенному вычислению.

Для этого:

1) подбирают близкое к значение, где достаточно просто найти значение функции;

2) считают, что приращение функции в точкеприблизительно равно дифференциалу в этой точке:

, то есть , где;

3) отсюда .

Пример 8. Найти приближенно .

Здесь , , ,

,

, .

Тогда .

Пример 9. Найти приближенно значение функции при.

Решение. Примем и. Для использования формулынайдем:

,

.

Тогда приближенное значение функции равно .

Посмотрим, на сколько отличается точное значение функции от найденного приближенного значения. Найдем точное значение функции:

.

Разность между точным 39,583005 и приближенным значением 39,59 функции в точкеесть б.м. величина 0,006995.