
- •Математика
- •Модуль 1. Дифференциальное исчисление функции одной переменной
- •Тема 1. Функции одной переменной, свойства и графики
- •1. Определение функций одной переменной
- •3. Элементарные функции
- •4. Основные свойства функций Возрастающие и убывающие функции
- •Взаимно обратные функции
- •Четные и нечетные функции
- •5. Преобразования графиков функций
- •Контрольные вопросы
- •Тема 2. Предел и непрерывность функции одной переменной
- •Введение
- •1. Предел функции в точке и на бесконечности
- •2. Основные свойства пределов
- •3. Бесконечно малые и бесконечно большие функции
- •4. Раскрытие неопределенностей ,
- •5. Первый и второй замечательные пределы
- •6. Эквивалентные бесконечно малые функции
- •7. Непрерывность функции, точки разрыва
- •8. Свойства функций, непрерывных на отрезке
- •Свойства функций, непрерывных на отрезке
- •Контрольные вопросы
- •Тема 3. Производные и дифференциалы. Экстремумы функции одной переменной
- •1. Определение производной
- •2. Геометрический и экономический смысл производной
- •2.1. Геометрический смысл производной и уравнение касательной
- •2.2. Экономический смысл производной
- •3. Основные правила дифференцирования
- •4. Таблица основных формул дифференцирования
- •5. Производные высших порядков
- •6. Вычисление пределов с помощью производных
- •А) ; б).
- •7. Дифференциал функции
- •Геометрический смысл дифференциала функции
- •8. Свойства дифференциала функции
- •9.2. Приближенное вычисление приращения функции
- •10. Дифференциалы высших порядков
- •11. Монотонность функции
- •12. Экстремумы (максимумы и минимумы) функции
- •3. Наибольшее и наименьшее значения непрерывной функции на отрезке
- •Контрольные вопросы
Математика
Раздел «Математический анализ»
Модуль 1. дифференциальное исчисление функции одной переменной
Содержание
Тема 1. Функции одной переменной, свойства и графики
Определение функций одной переменной.
Способы задания функций одной переменной.
Элементарные функции.
Основные свойства функций.
Преобразования графиков функций
Тема 2. Предел и непрерывность функции одной переменной
Предел функции в точке и на бесконечности.
Основные свойства пределов.
Бесконечно малые и бесконечно большие функции.
Раскрытие неопределенностей
 ,
,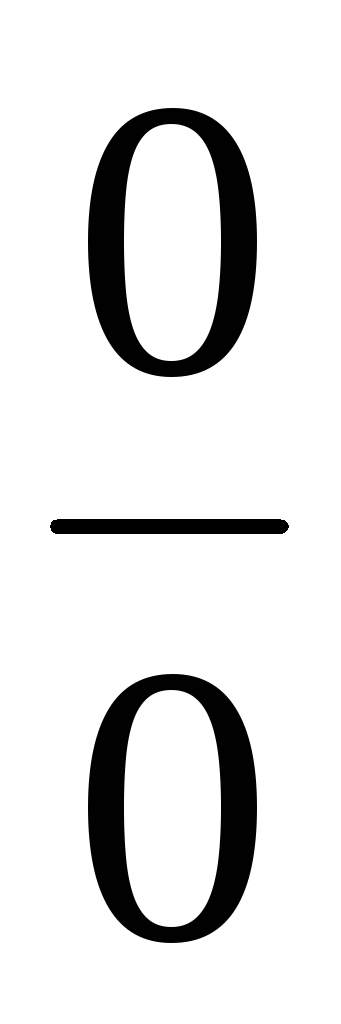 .
.Первый и второй замечательные пределы
Эквивалентные бесконечно малые функции
Непрерывность функции, точки разрыва
Свойства функций, непрерывных на отрезке.
Тема 3. Производные и дифференциалы. Экстремумы функции одной переменной
Определение производной.
Геометрический и экономический смысл производной.
Основные правила дифференцирования.
Таблица основных формул дифференцирования.
Производные высших порядков.
Вычисление пределов с помощью производных.
Дифференциал функции.
Свойства дифференциала функции.
Применение дифференциала к приближенным вычислениям.
Дифференциалы высших порядков
Монотонность функции.
Экстремумы (максимумы и минимумы) функции.
Наименьшее и наибольшее значения непрерывной функции на отрезке.
Модуль 1. Дифференциальное исчисление функции одной переменной
Тема 1. Функции одной переменной, свойства и графики
Содержание
Определение функций одной переменной.
Способы задания функций одной переменной.
Элементарные функции.
Основные свойства функций.
Преобразования графиков функций.
Понятие функции применяется не только в математике, но и в других областях знаний. В философии функция (лат. function – исполнение) – обязанность, круг деятельности1.
Функцией в общественных науках обычно называют предназначение, роль какого-либо элемента в социальной системе, или, иными словами, определенного вида работу, которая требуется от него в интересах системы в целом.
В менеджменте функция означает исполнение, совершенствование, служебную обязанность, назначение, роль. В широком смысле «функция» - это устойчивый вид деятельности, то, что обязан выполнять сотрудник независимо от своего желания.
1. Определение функций одной переменной
Дадим определение функции одной переменной.
Функцией (отображением), заданной на множестве
 ,
называется правило
,
называется правило
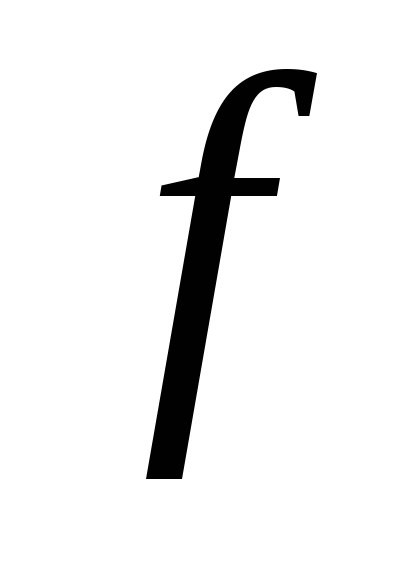 ,
по которому каждому элементу
,
по которому каждому элементу множества
множества
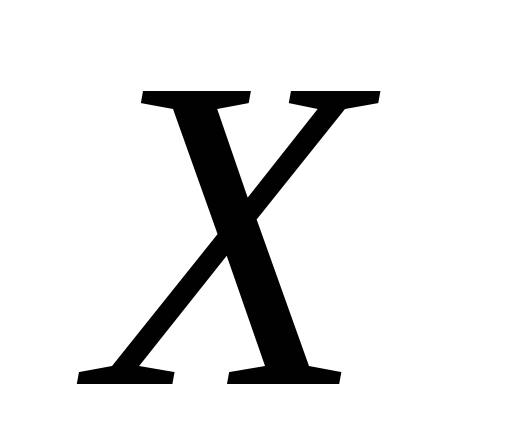 ставится в соответствие единственный
элемент
ставится в соответствие единственный
элемент
 множества
множества
 .
Используется запись
.
Используется запись
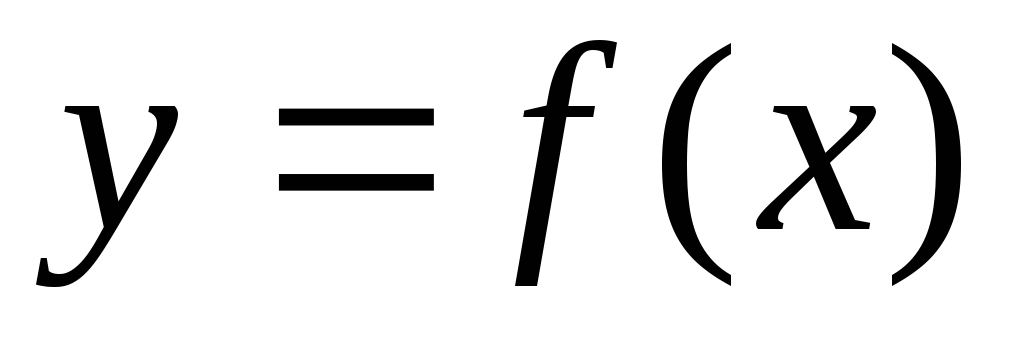 .
.Множество
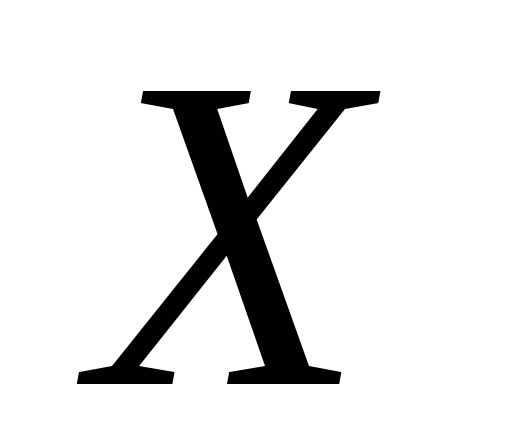 называетсяобластью
определения
функции
называетсяобластью
определения
функции
 ,
а множество
,
а множество –областью
значений
–областью
значений
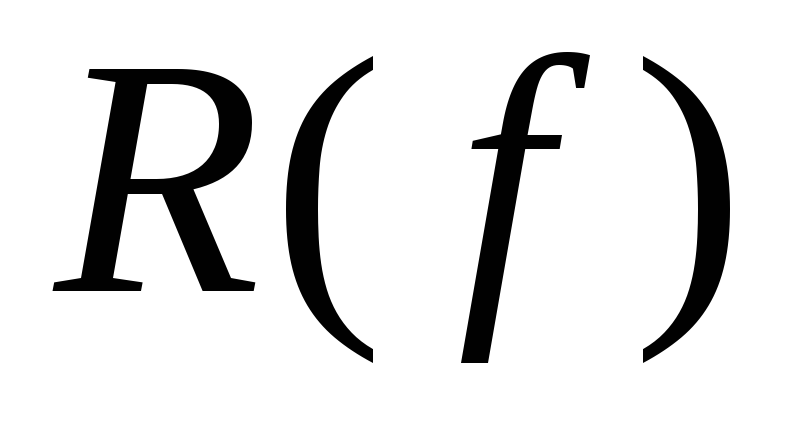 .
Элемент
.
Элемент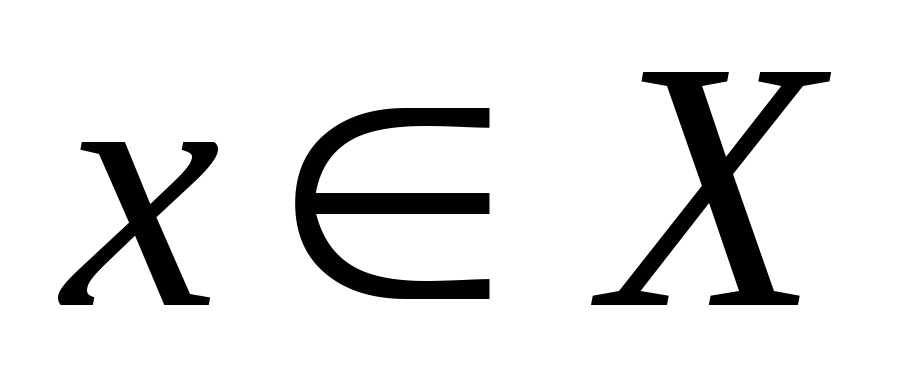 называетсяаргументом,
или независимой переменной, а
соответствующий элемент
называетсяаргументом,
или независимой переменной, а
соответствующий элемент
 -значением
функции,
или зависимой переменной.
-значением
функции,
или зависимой переменной. Если
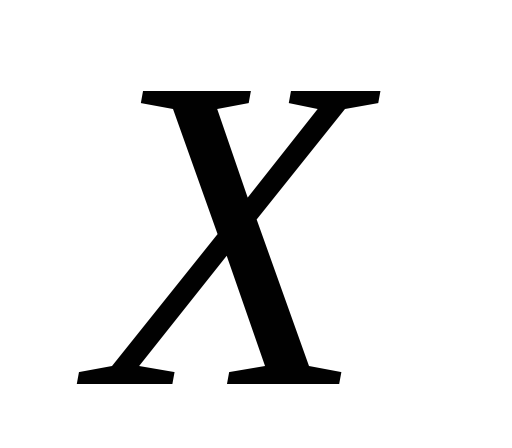 и
и
 являются числовыми множествами, то
являются числовыми множествами, то
 называетсячисловой
функцией
одной переменной.
называетсячисловой
функцией
одной переменной.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Рис. 1 – Математическое определение функции
Областью определения
 числовой функции одной переменной
числовой функции одной переменной
 является числовые промежутки на
действительной оси:
является числовые промежутки на
действительной оси: ,
отрезок
,
отрезок ,
интервалы
,
интервалы ,
, ,
,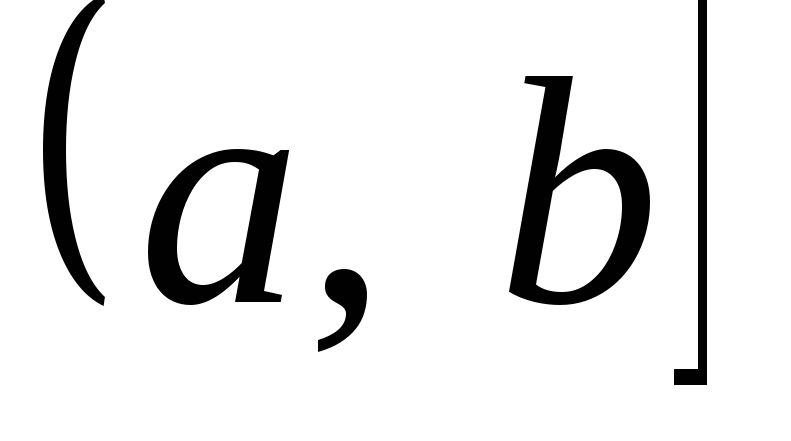 ,
или их объединение.
,
или их объединение.
Пример 1.
![]() ,
область определения
,
область определения![]() .
.
Пример 2.
![]() ,область
определения
,область
определения
![]() .
.
Пример 3.
![]() .
.
Решение.
Так как
![]() ,
то ее область определения
,
то ее область определения![]() ,
где
,
где![]() ,
а
,
а![]() .
.
Тогда
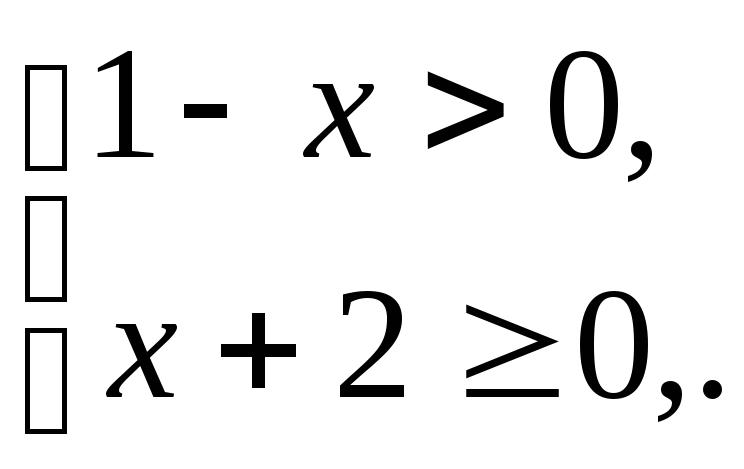
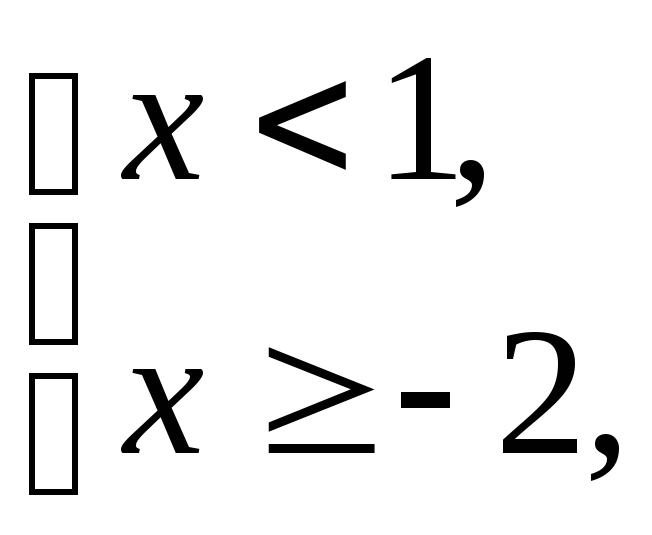
![]() .
.
Основными способами задания функций являются аналитический, табличный, графический. Существует и другие способы задания функций - алгоритмический, с помощью программы на ЭВМ.
Аналитический способ задания функции – имеется формула, указывающая, какие действия нужно произвести над аргументами, чтобы получить значение функции. Аналитический способ может быть явным и неявным.
Функция задана явно, если она задана:
одной формулой, разрешенной относительно зависимой переменной (например, у =
 или
или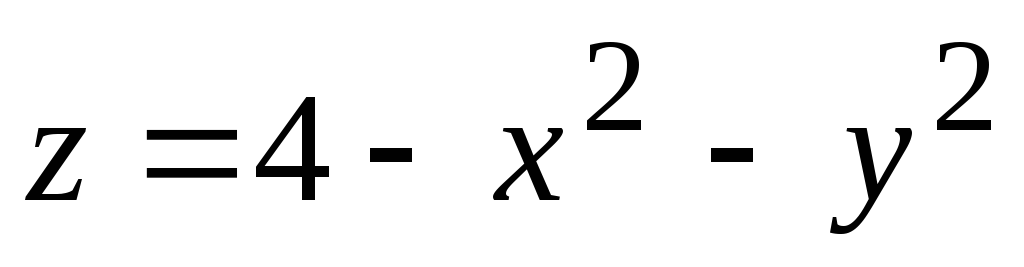 ),
или
),
илиразными формулами на определенных числовых промежутках (кусочно-аналитическое задание функции): например,
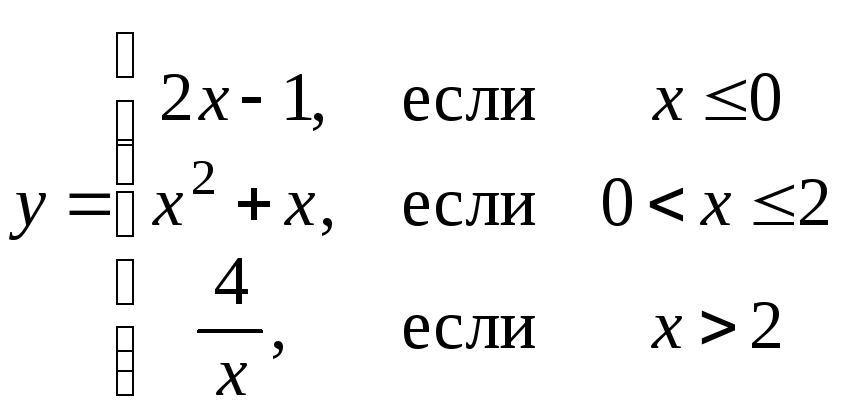 или
или
Пример 4.
Вычислить значения функции
 при
при![]() ,
,![]() ,
,![]() .
.
Решение.
![]() ;
;
![]() ;
;
![]() .
.
Функция одной или
двух переменных называется неявной,
если она задана уравнением, не разрешенной
относительно зависимой переменной.
Например,
![]() ,
или
,
или
![]() .
.
Табличный способ задания функции - с помощью таблицы, в которой указаны значения аргументов и соответствующие им значения зависимой переменной. Например, таблицы Брадиса.
Достоинством табличного способа является то, что по таблице можно непосредственно найти значение функции для имеющихся в таблице значений аргумента, а недостатком – отсутствие значений функции для промежуточных значений аргумента.
Таблица функции одной переменной
|
|
|
|
… |
|
|
|
|
|
… |
|
Графический способ задания функции.
Для функции одной переменной:
Графиком функции
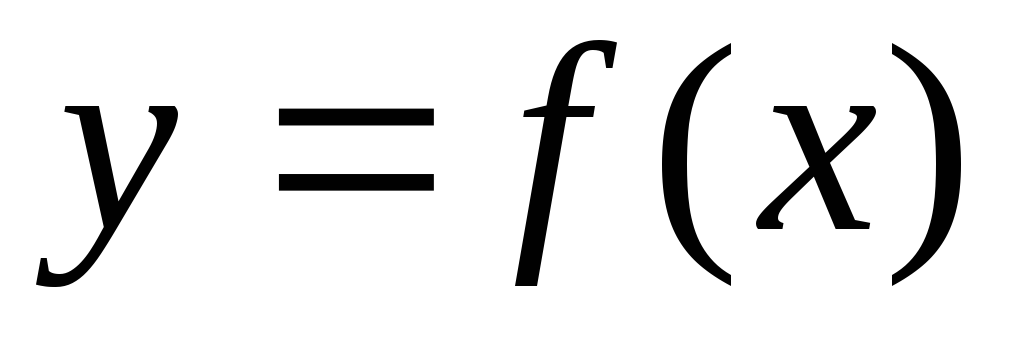 называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением
называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением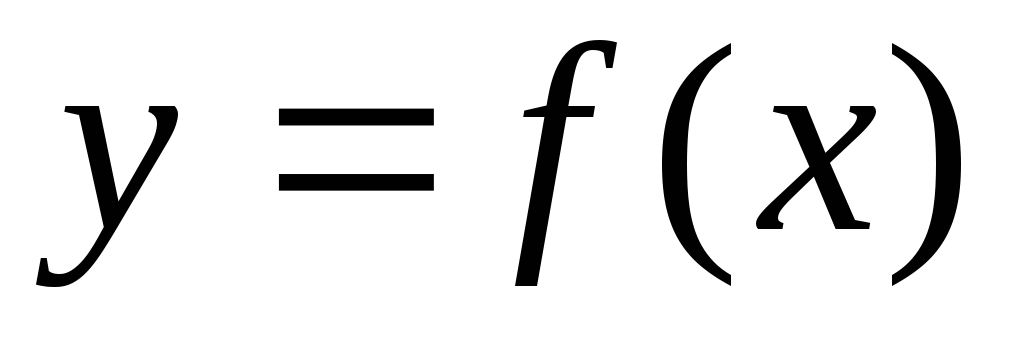 .
Равенство
.
Равенство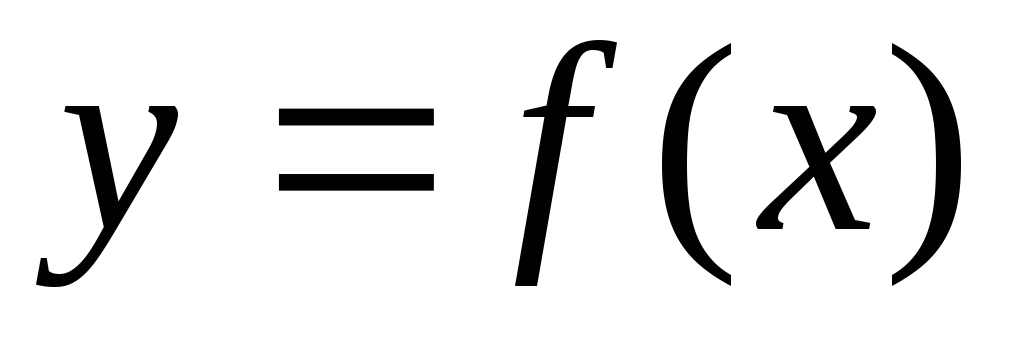 называетсяуравнением
этого графика.
называетсяуравнением
этого графика.
Отличительной
чертой любого графика функции
![]() является то, что каждая прямая
является то, что каждая прямая![]() (для
(для![]() из области определения), параллельная
оси ординат
из области определения), параллельная
оси ординат![]() ,
пересекает график вединственной
точке.
,
пересекает график вединственной
точке.
Пример 5.
Функция «абсолютная
величина
![]() »:
»:
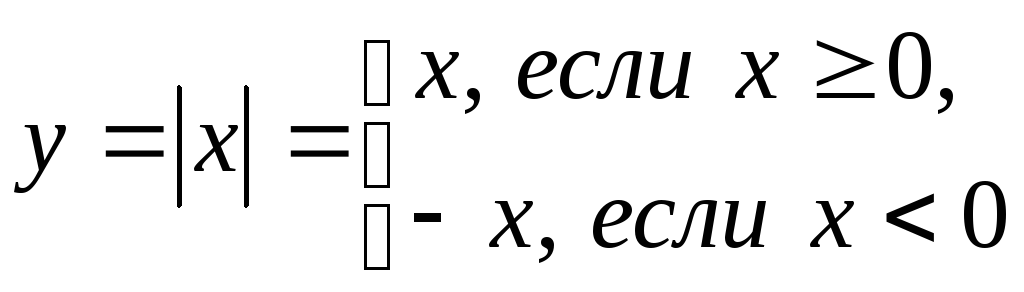 .
.
Функция задана с
помощью двух функций на разных числовых
промежутках. Поэтому график функции
«склеен» из двух графиков – графика
![]() на промежутке
на промежутке![]() и графика
и графика![]() на промежутке
на промежутке![]() .
.
![]()

![]()
![]()
![]()
![]()
