19

Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Сибирский государственный технологический университет»

О. А. Шушерина

Математика

Сборник задач к практическим занятиям (1-й семестр)

Направления подготовки

39.03.02 Менеджмент (группы 81–1, 2, 5),

38.03.03 Управление персоналом (группы 81-6, 9, 12, 13)

Квалификация выпускника – академический бакалавр

Красноярск

2014-15 уч. год

Содержание практических занятий

Модуль 1. Линейная АЛГЕБРА

6 недель, 3 лекции, 6 практич. занятий

1. Проверочная работа по школьному курсу 2 ч

2. Матрицы, операции над ними 2 ч

3. Определители: вычисление и свойства 2 ч

4. Системы линейных уравнений. Метод определителей (Крамера) 2 ч

5. Системы линейных уравнений. Метод исключения неизвестных (Гаусса) 2 ч

6. Контрольная работа № 1 «Линейная алгебра» 2 ч

Модуль 2. Векторы и аналитическая геометрия

6 недель, 3 лекции, 6 практич. занятий

7. Векторы на плоскости 2 ч

8. Прямая на плоскости 2 ч

9. Взаимное расположение прямых. Графическое решение систем линейных неравенств.

10. Кривые второго порядка 2 ч

11. Контрольная работа № 2 «Векторы и аналитическая геометрия» 2 ч

12. * Задачи с экономическим содержанием 2 ч

Модуль 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

6 недель, 3 лекции, 6 практич. занятий

13. Функции одной переменной: область определения и значений, свойства функции 2 ч

14. Графики функций одной переменной 2 ч

15. Предел функции 2 ч

16. Контрольная работа №3 «Введение в математический анализ» 2 ч

17. Зачетное занятие 2 ч

18. Зачетное занятие 2 ч

Модуль 1. Линейная алгебра

Практическое занятие 1.

проверочная работа по школьному курсу

Тема «Линейные уравнения и неравенства, их системы»

Образец варианта

Часть 1. Линейные уравнения и их системы

№1. (1 балл) Какое из уравнений является линейным уравнением с двумя переменными?

А) 3х + 5у = 10; Б) ху = 20; В) 4х + 3 = 15; Г) х+у=17.

№2. (1 балл) Через какую из данных точек проходит график функции х + 4у = 14?

А) А(6; 3); Б) В(-10; 6); В) С(7; 7); Г) К(0; 4).

№3. (1 балл) Какая из пар чисел является решением системы уравнений ?

А) (-2; 0); Б) (0; -5); В) (3; 1); Г) другой ответ.

№4. (2 балла) Решите систему уравнений: .

№5. (3 балла) Постройте график функции . Пользуясь построенным графиком, установите, при каких значениях аргумента функция принимает положительные значения.

Часть 2. Линейные неравенства и их системы

№1. (1 балл) Если , то для любыхиверно неравенство:

№2. (1 балл) Решите неравенство .

№3. (2 балла) Найдите наименьшее целое решение системы

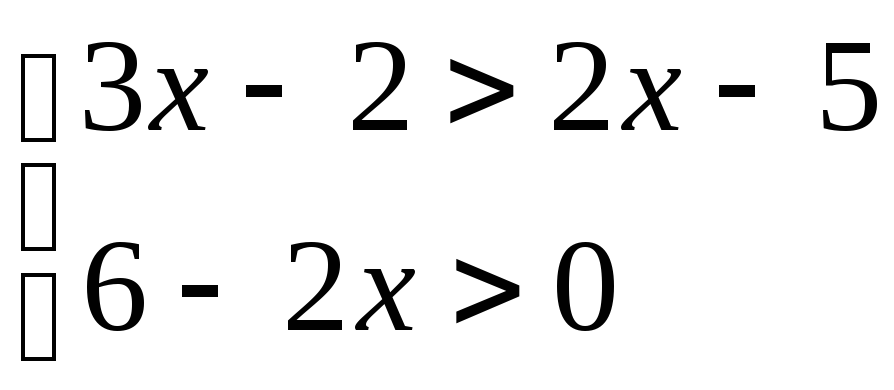
№4. (3 балла) Для каждой системы неравенств укажите множество ее решений.

1. 2.3.

А. (-2; 4]; Б. [-2; -1]; В [-3; 5]; Г. (-∞; 2].

Практическое занятие 2.

Матрицы, операции над ними

Задачи для решения на занятии

№1. Даны матрицы ,и единичная матрица.

Найти матрицы ,;,,,,,.

1) ;

2) .

№2. Найти произведение матриц.

1) 2)

3) 4).

Задачи для домашнего решения

№3. Даны матрицы А, В и единичная матрица Е.

Найти матрицы ,,,,,,.

1) ; 2).

№4. Найти произведение матриц.

1) 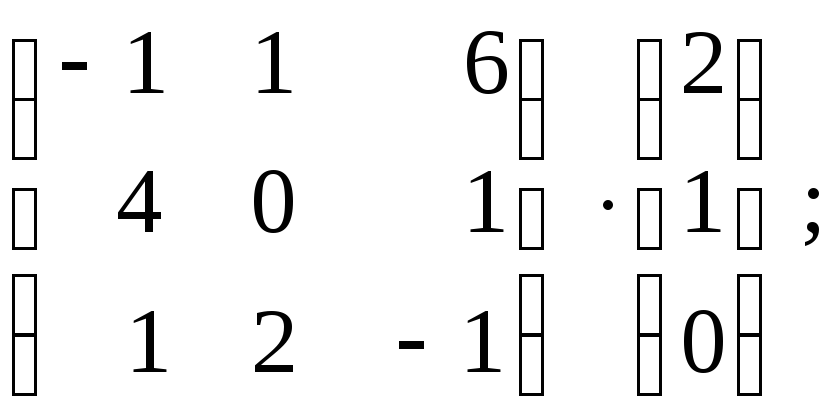2);

3) ; 4).

№5. Даны матрицы и. Найти матрицу, являющуюся решением уравнением.

Практическое занятие 3.

Определители: вычисление и свойства

Задачи для решения на занятии

№1. Вычислить определители второго порядка:

1) ; 2) ; 3) ; 4) ; 5) .

№2. Вычислить определители третьего порядка по правилу треугольников.

1) 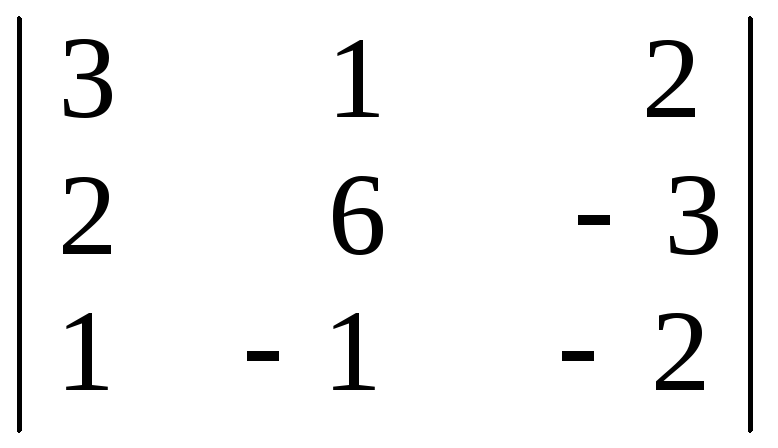; 2).

№3. Дан определитель . Вычислить все алгебраические дополнения для элементов; а) первой строки, б) второго столбца.

№4. Вычислить определители, используя теорему о разложении по элементам строки или столбца.

1) ; 2).

Задачи для домашнего решения

№5. Вычислить определители второго порядка:

1) ; 2) ; 3); 4) ; 5) .

№6. Найти, при каком значении определительравен нулю.

№7. Вычислить определители третьего порядка двумя способами:

а) по правилу треугольников; б) используя теорему о разложении.

1) ; 2).

№8. Записать выражение для определителя .

Практическое занятие 4.

Системы линейных уравнений. Метод Крамера

Задачи для решения на занятии

Решение задач по новому материалу.

Для решения заданий студенту необходимо:

1) знать алгоритмрешения СЛУ методом определителей (Крамера);

2) формулировать признакисовместной, несовместной, определенной и неопределенной СЛУ (с помощью определителей);

3) уметь находить значения неизвестных по формуламКрамера;

4) уметь записывать общее решениев случае неопределенной СЛУ.

№2. Решите системы 2-х линейных уравнений с двумя неизвестными методом Крамера (определителей). Обоснуйте, какая СЛУ определенная, несовместная или неопределенная. В случае единственного решения системы выполните проверку.