Физика ИДЗ 1 (ч.1)

1.33. Движение точки по окружности радиусом R = 4 м задано уравнением S = 10 + t2 - 2t. Найти тангенциальное a , нормальное an и полное а ускорения точки в момент времени t = 2 с.

1.34. Движение материальной точки задано уравнением Х = 4t - - 0,05t2. Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение точки в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

1.35.Путь, пройденный телом, задан уравнением S = 2t – t2 + t3 (м). Найти среднюю скорость тела в интервале от 1 до 5 с.

1.36.Путь, пройденный телом, задан уравнением S = 2 + 12t - -6t2 + 4t3 (см). Найти среднее ускорение тела в интервале от 1 до 4 с.

1.37. Путь, пройденный точкой по окружности радиусом R = 7 см, задан уравнением S = 4 + 2t + 0,5t2 (см). Определить полное ускорение a точки к концу пятой секунды.

1.38.Частота маховика уменьшалась с n0 = 10 об/с до n = 6 об/с. За время торможения он сделал N = 50 оборотов. Определить угловое ускорение маховика и продолжительность торможения t.

1.39.Тело вращается вокруг неподвижной оси. Угол поворота задан уравнением φ = 6t -2t3. Найти угловое ускорение тела в

момент его остановки.

1.40.Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с2. Через какое время после начала движения нормальное ускорение точки станет в 2 раза больше тангенциального?

1.41.Диск радиусом R = 0,2 м вращается вокруг фиксированной

оси, проходящей через его геометрический центр. Зависимость угла поворота от времени задана уравнением φ = 3 + 0,1t3 - t. Определить

для момента времени t = 5 с тангенциальное a , нормальное an и

полное а ускорения точек на краю диска.

1.42. Точка движется по окружности с угловым ускорением ε ~ t. При t = 0 угловая скорость ω = 0. Модуль нормального ускорения

точки an ~ tk. Найти значение показателя k.

1.43. Зависимость угла поворота тела вокруг неподвижной оси от времени задана уравнением φ = A + Bt + Ct2 , где A = 10 рад, B = 20 рад/c, С = -2 рад/c2. Найти для момента времени t = 4 c полное ускорение точки, находящейся на расстоянии R = 1 м от оси вращения.

1.44. На цилиндр радиусом R = 4 см, который может вращаться около неподвижной горизонтальной оси, намотана нить. К концу нити привязали груз и предоставили ему возможность опускаться. За время

11

t = 3 с груз опустился на высоту h =1,5 м. Определить угловое ускорение цилиндра.

1.45. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a = 5 cм/с2. Через какое

время после начала движения нормальная составляющая ускорения an = 2 a ?

1.46.Камень брошен с начальной скоростью V0 = 19,6 м/с под углом α = 300 к горизонту. Определить радиус кривизны траектории движения R в высшей ее точке.

1.47.Тело брошено со скоростью V0 = 20 м/с под углом α = 300 к

горизонту. Определить нормальную составляющую ускорения тела an

через время 1,5 с после начала движения.

1.48. Камень брошен горизонтально со скоростью V0 = 10 м/с. Чему равна нормальная составляющая ускорения камня an через две

секунды после начала его движения?

1.49. Тело брошено под углом к горизонту. Радиус кривизны траектории движения тела и его скорость связаны соотношением R ~ Vk. Найти значение показателя степени k. Сопротивлением воздуха пренебречь.

воздуха пренебречь.

1.51. Лодка стоит на расстоянии S = 8 м от отвесного берега реки. Высота берега h = 6 м. С берега на лодку бросают груз. С какой скоростью V0 надо бросить груз, чтобы его скорость при ударе о лодку была минимальной? Под каким углом к горизонту необходимо бросить груз?

1.52.Мяч бросают в стенку, находящуюся на расстоянии S = 20 м

c начальной скоростью V0 = 20 м/с. Какой наибольшей высоты при ударе о стенку может достичь мяч? Под каким углом к горизонту его надо бросать в этом случае?

1.53.С башни высотой h = 10 м со скоростью V0 = 10 м/с бросают мяч. На какое наибольшее расстояние от основания башни может улететь мяч? Под каким углом к горизонту его надо в этом случае

бросать?

1.54. Шарик падает без начальной скорости на поверхность наклонной плоскости, составляющей угол α = 300 с горизонтом. Расстояние по вертикали от начального положения шарика до точки удара с плоскость h = 80 см. Считая удар шарика о плоскость

12

абсолютно упругим и пренебрегая возможным вращением шарика, найти наибольшее его удаление от плоскости.

2. ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ

Уравнение движения материальной точки (второй закон Ньютона) в векторной форме:

ddtp F.

При m const уравнение примет вид ma F .

действующих на точку, P mV - импульс, m - масса, V - скорость и a - ускорение материальной точки.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Тело массой m 2 кг движется по вертикальной стене.

Ось OY направим вертикально вверх, ось OX – перпендикулярно стене. В проекциях на оси координат уравнение (1) примет вид

ma F1 cos mg F1 sin .

13

y

F1

N

x

Задача 2. В лифте, движущемся вертикально вверх с ускорением 0,2 м/с 2, вращается столик с угловой скоростью рад/с. На столике лежит брусок, коэффициент трения равен 0,1. Найти максимальное расстояние между бруском и осью вращения, при котором он

удерживается на столике. Принять g = 9,8 м/c 2, 2 10.

Брусок участвует в двух движениях одновременно: поступательно движется вверх с ускорением a1 и вращается вокруг

неподвижной оси с центростремительным ускорением an . Запишем II

14

закон Ньютона для бруска:

ma mg N FTP , где a an a1 .

Выберем оси координат OX и OY. В координатной форме основное уравнение движения примет вид

где an = 2 R , FTP = N . Из (2) N = m (a1 + g),

FTP = m a1 g .

Перепишем (1): m 2 R m a1 g .

Получим, что

R (a1 g) .

После подстановки данных и вычислений R = 0,1 м. Ответ: R = 0,1 м.

Задача 3. С вертолёта, неподвижного висящего на некоторой высоте над поверхностью земли, сброшен груз массой m.

Считая, что сила сопротивления воздуха изменяется пропорционально скорости (Fсопр = kV), определить, через какой промежуток времени ускорение груза a1 = g/2. Коэффициент сопротивления k = const.

Учитывая, что a = dV / dt , Fсопр= kV , получим дифференциальное уравнение первого порядка с

разделяющимися переменными: m dVdt mg kV ,

dVdt g mk V ,

15

ln mgkV 1 mk t.

Получим:

mgkV 1 e ktm .

Отсюда

После логарифмирования:

ln 2 mk t1 .

Получим

если коэффициент трения тела о плоскость μ = 0,2?

16

2.2.Автомобиль массой m = 2,5 т поднимается в гору ( 300) ускоренно и за время t = 5 мин проходит путь S = 9 км. Начальная

скорость автомобиля V0 = 1 м/с. Какова сила тяги мотора автомобиля

F?

2.3.Брусок соскальзывает с наклонной плоскости, образующей с горизонтом угол α = 300. Каково ускорение бруска, если коэффициент трения его о поверхность плоскости μ = 0,4?

2.4.За какое время тяжелое тело спустится с вершины наклонной плоскости, высота которой h = 2 м, угол наклона α = 450? Предельный угол, при котором тело находится в покое, для этой плоскости равен

300.

2.5.Наклонная плоскость образует с горизонтом угол α = 300. Ее длина l 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой

плоскости за время t = 2 с. Определить коэффициент трения тела о плоскость μ.

2.6. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 300. Ее длина l 2 м, коэффициент трения тела о

плоскость μ = 0,2. Какова скорость тела в конце наклонной плоскости, если его начальная скорость V0 = 0?

2.7. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 300. Зависимость пройденного телом расстояния S от времени t дается уравнением S = ct2, где с = 1,5 м/с2. Найти коэффициент трения тела о плоскость μ.

2.8. На наклонной плоскости длиной l 13 м и высотой h = 5 м лежит груз массой m = 26 кг. Коэффициент трения груза о плоскость μ = 0,5. Какую силу F надо приложить к грузу: а) чтобы втащить груз; б) чтобы стащить груз?

2.9.Мальчик тянет по горизонтальной дороге санки с грузом. С

каким ускорением a движутся санки, если сила тяги F = 200 Н, а веревка образует с горизонтом угол α = 450? Масса санок m = 50 кг. Коэффициент трения полозьев санок μ = 0,1.

2.10.Два связанных груза массами m1 = 3 кг и m2 = 5 кг лежат на горизонтальном столе, шнур разрывается при натяжении Т = 24 Н.

Какую максимальную силу F можно приложить к грузу массой m1? Коэффициент трения принять равным μ = 0,2.

2.11.Ракета движется в поле силы тяжести Земли: а) вниз с возрастающей скоростью; б) вверх с торможением. В каждом случае сравнить вес тела, лежащего на полу ракеты, с силой тяжести.

2.12.Шарик массой m висит на нити, которая закреплена. С каким ускорением a и в каком направлении следует перемещать точку

17

подвеса, чтобы натяжение нити было равно половине силы тяжести шарика?

блок. Определить коэффициент трения между столом и грузом массой m2, если ускорение грузов a 5,4 м/с2.

2.17. Невесомый блок укреплен на конце стола. Грузы массами m1 = 1 кг, m2 = 2 кг соединены нитью, которая перекинута через блок. Найти коэффициент трения груза о стол, если сила давления на ось

блока F = 1 Н. Трение в блоке мало.

2.18.Невесомый блок укреплен на вершине наклонной

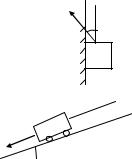
Fуглом наклона α = 300, прилагая силу,

направленную под углом β = 600 к

горизонту. Определить эту силу, еслиm

18

2.20.По столу тянут груз при помощи нити, прикрепленной к динамометру. Динамометр показывает 30 Н. Затем тот же груз приводят в движение при помощи нити, перекинутой через невесомый блок, на конце которой висит груз 3 кг. С одинаковым ли ускорением будет двигаться груз? Если нет, то чему равно отношение ускорений?

2.21.Тело массой m движется вверх по F вертикальный стене под действием силы F,

направленной под углом α к вертикали. Определить, с каким ускорением движется тело, если коэффициент трения тела о стенку равен μ?

принять равным μ = 0,01.

2.23.Маневровый тепловоз массой M = 100 т тянет два вагона массой по m = 100 т с ускорением a = 0,1 м/с2. Найти силу тяги тепловоза F и силу натяжения сцепок T, если коэффициент сопротивления, т.е. отношение силы сопротивления к силе реакции опоры, равен 0,006.

2.24.Ящик массой m = 10 кг перемещают по полу, прикладывая к нему силу F под углом α = 300 к горизонту. В течение времени τ = 1 с

скорость ящика возросла с V1 = 2 м/с до V2 = 4 м/с. Коэффициент трения скольжения между ящиком и полом μ = 0,15. Определить силу

F.

2.25.Два одинаковых бруска, связанные нитью, движутся по горизонтальной плоскости под действием горизонтальной силы F. Зависит ли сила натяжения нити: а) от массы брусков; б) от коэффициентов трения брусков о плоскость?

2.26.На тросе длиной l подвешено тело массой m. На какой

максимальный угол можно отклонить его, чтобы при движении груза трос не оборвался? Трос может выдерживать нагрузку, превосходящую силу тяжести тела в n раз.

2.27. Грузик, привязанный к шнуру длиной l 1,5 м, вращается в горизонтальной плоскости с частотой n = 28 об/мин. Какой угол с вертикалью образует шнур?

19

2.28.Велосипедист, движущийся в вертикальной плоскости со скоростью V = 36 км/ч, описывает мертвую петлю. Определить максимальный радиус петли R.

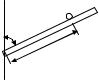
2.29.Шарик лежит на желобе, который может вращаться вокруг

2.30.Нить математического маятника отклонили до горизонтального положения и отпустили. Какова минимальная прочность нити F, если масса маятника m?

2.31.Самолет описывает мёртвую петлю радиусом R = 200 м. Во сколько раз сила, с которой летчик давит на сидение в нижней точке петли, больше силы тяжести летчика? Скорость самолета V = 100 м/с.

2.32.Грузик, привязанный к нити длиной l 1 м, вращается в

горизонтальной плоскости. Определить период вращения грузика T если нить отклонилась на угол 600от вертикали.

2.33.Найти отношение модуля силы натяжения нити математического маятника в крайнем положении с модулем силы натяжения нити конического маятника; длины нитей, массы грузиков

иуглы отклонения маятников одинаковы.

2.34.Гиря массой m = 100 г вращается на стержне в вертикальной плоскости с постоянной скоростью. На сколько отличается сила натяжения стержня при прохождении гири через нижнюю и верхнюю точки ее траектории движения?

2.35.Груз массой m = 25 кг подвешен на цепи длиной l 2,5 м с

прочностью на разрыв F = 500 Н. На какой угол можно отвести груз, чтобы цепь при качаниях груза не разорвалась?

2.36.Дорожка для велосипедных гонок имеет закругление радиусом R = 40 м. В этом месте дорожка сделана с наклоном в

= 300. На какую скорость V рассчитан такой наклон?

2.37.Самолет, летящий со скоростью V = 900 км/ч, делает "мертвую петлю". Каков должен быть ее радиус R, чтобы наибольшая сила давления летчика на сидение была в пять раз больше силы тяжести?

2.38.Гирька, привязанная к нити длиной l 25 см, вращается в

горизонтальной плоскости. Скорость вращения гирьки соответствует n = 2 об/с, масса ее m = 60 г. Найти натяжение нити F.

20