Физика ИДЗ 1 (ч.1)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

Кафедра физики и микроэлектроники

МЕХАНИКА

Домашнее задание №1

Волгодонск 2011 г

1. КИНЕМАТИКА

Положение материальной точки в пространстве задается радиус-

вектором r : r xi yj zk ,

где i , j, k - единичные векторы, x,y,z- декартовы координаты точки.

Быстроту изменения положения точки в пространстве с течением времени характеризует скорость.

Средняя скорость

V rt ,

где r - перемещение точки за время t .

Мгновенная скорость

V drdt Vxi Vy j Vz k ,

где Vx dxdt ;Vy dydt ;Vz dzdt .

Модуль скорости

V Vx2 Vy2 Vz2 .

Быстроту изменения вектора скорости с течением времени характеризует ускорение.

Среднее ускорение

a Vt .

Мгновенное ускорение a dVdt axi ay j azk ,

где ax dVdtx ; ay dVdty ; az dVdtz .

При движении точки вдоль оси OX

t

Vx V0 x 0 axdt ;

t

x x0 0Vxdt,

где V0X и х0 - скорость и координата в момент времени t=0.

3

При равнопеременном движении (aX=const) вдоль оси ОХ

Vx V0x axt;

xx0 V0xt ax2t 2 .

Вслучае криволинейного движения

a an a , an a ,

где an - нормальное ускорение, характеризует изменение скорости по

направлению и направлено к центру кривизны в данной точке траектории; a - тангенциальное ускорение, характеризует изменение

скорости по величине и направлено вдоль касательной в данной точке траектории.

Модуль полного ускорения a an2 a2 ,

где an V 2 , a dV , R - радиус кривизны траектории.

R dt

Положение твердого тела при вращении вокруг оси определяется углом поворота .

Средняя угловая скорость

t ,

где - изменение угла поворота за интервал времени t .

Мгновенная угловая скорость

ddt .

Угловое ускорение

d d 22 . dt dt

Кинематические уравнения при вращении твердого тела:

t

0 dt;

0

t

0 dt,

0

где 0 и 0 - начальные угловая скорость и угол поворота. При равнопеременном вращении

4

0 t;

0 0t t 2 .

2

Связь между линейными и угловыми величинами, характеризующими движение точки:

V R ; a R .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

времени t1=2 с и t2=4 с, а также среднюю скорость в интервале времени от t1 до t2.

Точка прямолинейно движется вдоль оси OX. Модуль мгновенной скорости в этом случае

V dx dt 5 0,4t 0,3t 2 (м/с).

Найдем V1 и V2:

V 9 м/с.

Ответ: V1=7 м/с, V2=11,4 м/с, V 9 м/с.

Задача 2. С башни высотой Н = 25 м бросили камень со

скоростью V0 = 15 м/с под углом 300 0 к горизонту. Через какое землювремя?tп и на каком расстоянии S от основания башни камень упадет на

Начало отсчета возьмем у основания башни.

5

Ось OY направим вертикально вверх, ось OX – горизонтально. Движение камня вдоль оси OX равномерное, вдоль оси OY – равнопеременное:

Общие уравнения движения камня в выбранной системе отсчета примут вид

Задача 3. Небольшое тело движется по окружности радиусом R со скоростью V=kt где k=const. Найти зависимость полного ускорения от времени.

На рисунке покажем полное ускорение тела и его составляющие. a an a , an a ;

a an2 a2 .

6

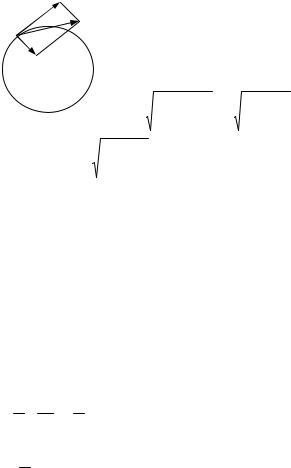
Модуль тангенциального ускорения

Задача 4. Найти величину углового ускорения лопатки турбины, расположенной на расстоянии R от оси вращения, через время t1 после

пуска турбины. Зависимость линейной скорости лопатки от времени

выражена уравнением V at bt 2 , где a и b - постоянные коэффициенты. Найти число оборотов N2 через время t2 после пуска турбины. Принять 0 0 .

Угловое ускорение

d dt.

Используем связь угловой скорости с линейной:

V R (aR)t (bR)t 2 .

Найдем зависимость углового ускорения от времени:

Ra 2Rb t R1 (a 2bt).

В момент времени t1

1 R1 a 2bt1 .

Угловая скорость

Выразив угол через число оборотов ( 2 N2 ) и зная как функцию времени, получим

7

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.1.Свободно падающее тело последние 196 м пути прошло за 4 с. Найти время падения.

1.2.Во сколько раз отличается время движения катера туда и обратно по реке и по озеру? Скорость течения реки 3 км/ч, скорость катера относительно воды в обоих случаях 9 км/ч. Расстояние считать одинаковым.

1.3.С какой высоты упало тело, если последний метр своего пути оно прошло за время t = 0,1 с?

1.4.Два тела свободно падают с разных высот и достигают земли одновременно. Первое тело падало в течение 2 с, второе - 1 с. На какой высоте было первое тело, когда второе начало падать?

1.5.С балкона бросили мяч вертикально вверх с начальной

скоростью V0 = 5 м/с. Через время τ = 2 c мяч упал на землю. Определить высоту балкона и модуль скорости мяча в момент удара о землю.

1.6.Два тела брошены вертикально вверх из одной точки, одно за

другим, через время τ = 2 с с начальной скоростью V01 = V02 = 30 м/с. Через какое время после бросания первого тела они встретятся?

1.7.Свободно падающее тело в последнюю секунду проходит половину всего пути. Определить высоту, с которой падает тело, и продолжительность его падения.

1.8.Тело, брошенное вертикально вверх, находилось на одной и той же высоте h = 8,75 м два раза с интервалом ∆t = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость тела.

1.9.Тело брошено вертикально вверх с начальной скоростью

V0 = 4 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с той же начальной скоростью V0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

8

1.10. Материальная точка движется прямолинейно с ускорением a 5 м/с2. Определить, на сколько путь, пройденный в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять

V0 = 0.

1.11. Поезд метро проходит перегон 2 км за 2 мин 20 с. Максимальная скорость поезда 60 км/ч. В начале и конце перегона поезд движется с постоянными ускорениями, равными по абсолютной величине. Определить эти ускорения.

1.12. Два тела свободно падают одно за другим с одной и той же высоты с интервалом времени τ. Через какое время от начала падения первого тела расстояние между ними будет равно l ?

1.13. Наблюдатель стоит в начале электропоезда. Первый вагон прошел мимо него за время τ =1 с. Какое время будет двигаться мимо него седьмой вагон? Движение поезда равноускоренное, его начальная скорость V0 = 0.

1.14. Камень брошен вертикально вверх с начальной скоростью V0 = 20 м/с. Через сколько секунд камень будет находиться на высоте h = 15 м? Какова будет скорость V камня на этой высоте? Сопротивлением воздуха пренебречь.

1.15. С вышки бросили камень в горизонтальном направлении. Через время τ = 2 c он упал на землю на расстоянии S = 40 м от основания вышки. Определить начальную V0 и конечную V скорости камня.

1.16. Горизонтально брошенный мяч ударяется о стенку, находящуюся на расстоянии S = 5 м от нее. Высота места удара мяча о стенку на h 1 м меньше высоты, с которой брошен мяч. Под каким углом α мяч подлетает к поверхности стенки? Сопротивление воздуха не учитывать.

1.17.Тело брошено под углом к горизонту. Наибольшая высота подъема и радиус кривизны траектории движения тела в верхней точке траектории равны 3 м. Найти начальную скорость тела и угол, под которым его бросили. Сопротивление воздуха не учитывать.

1.18.Дальность полета тела, брошенного горизонтально со

скоростью V0 = 10 м/с, равна высоте, с которой брошено тело. Чему равна эта высота?

1.19.Тело, брошенное под углом α = 300 к горизонту, дважды

было на одной и той же высоте h: спустя t1 = 10 с и t2 = 50 с. Определить начальную скорость тела и высоту его подъема.

1.20.Пуля пущена с начальной скоростью V0 = 200 м/с под углом

α= 600 к горизонту. Определить максимальную высоту подъема h и радиус кривизны траектории R пули в ее наивысшей точке.

9

1.21.Тело брошено под некоторым углом α к горизонту. Найти величину этого угла, если горизонтальная дальность полета тела S в 4 раза больше максимальной высоты траектории h.

1.22.Камень брошен горизонтально. Через время 3 с вектор

его скорости V образует с горизонтом угол α = 600 . Какова была

начальная скорость V0 камня?

1.23. Камень брошен под углом α = 600 к горизонту cо скоростью V0 =20 м/с. Вычислить нормальную составляющую ускорения камня через время 0,5 с после начала движения.

1.24.Дальность полета тела, брошенного горизонтально со

скоростью V0 = 10 м/с, равна высоте, с которой брошено тело. Под каким углом к α горизонту тело упадет?

1.25.Мальчик бросает мяч со скоростью V0 = 10 м/с под углом

α= 450 к горизонту. На какой высоте мяч ударится о стенку, если она находятся на расстояния S = 3 м от мальчика?

1.26.С башни высотой h = 20 м горизонтально бросают мяч со

скоростью V0 = 10 м/с. На каком расстоянии S от башни мяч упадет на землю?

1.27. Маховик начал вращаться равноускоренно и за время10 с его частота стала n = 300 об/мин. Найти угловое ускорение

маховика и число оборотов, которое он сделал за это время.

1.28. Точка движется по окружности радиусом R = 10 м с постоянным тангенциальным ускорением a , если известно, что к

концу пятого оборота скорость точки V = 80 см/с. Найти a .

1.29. Колесо автомашины вращается равноускоренно. После 50 полных оборотов частота вращения колеса возросла от n1 = 4 об/с до n2 = 6 об/с. Определить угловое ускорение колеса .

1.30. Движение точки по окружности радиусом R = 200 см задано уравнением S = 2t3 (м). В какой момент времени нормальная составляющая ускорения an точки будет равна ее тангенциальной составляющей a ? Определить полное ускорение а в этот момент.

1.31. Движение точки в плоскости XY задано уравнениями X = 2t–0,5t3 (м), Y = 2t – t2 (м). Определить скорость точки V к концу второй секунды.

1.32. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени нормальная составляющая ускорения an = 4,0 м/с2, а векторы полного и нормального ускорений образуют угол α = 600. Найти скорость и тангенциальную составляющую ускорения точки.

10