
- •«Национальный исследовательский ядерный университет «мифи»
- •Элементарные свойства рядов
- •Признаки сходимости
- •Числовые ряды с положительными членами
- •1Й признак сравнения
- •II признак сравнения (предельный)
- •Признак сходимости Даламбера
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •Знакочередующиеся числовые ряды
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «мифи»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Конспект лекций
по теме:
«Числовые ряды»

Волгодонск
Числовые ряды
Определение: Рассмотрим бесконечную числовую последовательность:
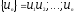 числовым рядом
называется выражение
числовым рядом
называется выражение
 ,
где
,
где – общий член ряда.
– общий член ряда.
Пример:
 -знакоположительный
ряд
-знакоположительный
ряд
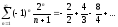 -знакочередующийся
ряд
-знакочередующийся
ряд
Последовательность
 ,
где
,
где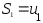 ;
;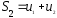 ;
; -последовательность
частичных сумм ряда.
-последовательность
частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой
ряд
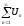 называетсясходящимся,
если существует конечный
называетсясходящимся,
если существует конечный
 ,
то ряд называется расходящимся
и суммы S
не имеют.
,
то ряд называется расходящимся
и суммы S
не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
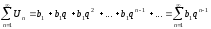 ,
где n
– частичная сумма ряда
,
где n
– частичная сумма ряда
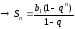 -
суммаn
первых членов геометрической прогрессии.
-
суммаn
первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1)
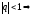 геометрическая
прогрессия убывающая.
геометрическая
прогрессия убывающая.

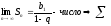 сходится
и имеет сумму
сходится
и имеет сумму

2)
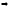

3)


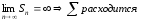

 =
не существует – ряд расходится.
=
не существует – ряд расходится.
Вывод:
ряд из членов геометрической прогрессии
сходится если
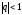 и
расходится
и
расходится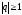

Элементарные свойства рядов
1)
Если
 (1)
сходится и имеет суммуS,
то
(1)
сходится и имеет суммуS,
то
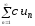 (2)
тоже сходится, и имеет суммуCS,
где С-const.
(2)
тоже сходится, и имеет суммуCS,
где С-const.
Доказательство:
Пусть
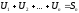 ,n–
ая частичная сумма 1 ряда.
,n–
ая частичная сумма 1 ряда.
 ,
n–ая
частичная сумма 2 ряда.
,
n–ая
частичная сумма 2 ряда.
Т.к
1 ряд сходится, то
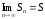 .
.
Рассмотрим
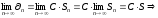 (2)
ряд сходится.
(2)
ряд сходится.
Конец доказательства.
2)
Если
 (1)
сходится с суммойS1,
и
(1)
сходится с суммойS1,
и
 (2)
сходится с суммойS2.
(2)
сходится с суммойS2.
 тоже
сходится с суммой
тоже
сходится с суммой
 .
.
Доказательство:
Обозначим
 -n
– частичная сумма 1 ряда.
-n
– частичная сумма 1 ряда.
 - n
– частичная сумма 2 ряда.
- n
– частичная сумма 2 ряда.


Рассмотрим n-ую частичную сумму ряда
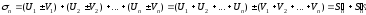

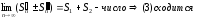 и
сумма
и
сумма
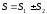 .
.
Конец доказательства.
3) Любой ряд может быть представлен в виде:
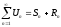 ,
где
,
где
 -n
– частичная сумма
-n
– частичная сумма
 - n
– остаток ряда.
- n
– остаток ряда.
n
– остаток ряда
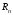 тоже
является рядом.
тоже
является рядом.
Если
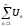 ,
то и его остаток
,
то и его остаток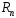 тоже сходится.
тоже сходится.
Доказательство: доказательство этого факта следует из того, что сумма ряда и сумма его остатка отличаются друг от друга на конечное число cлагаемых.
Конец доказательства.
Следствие: на сходимость ряда не влияет отбрасывание или приписывание в начало ряда конечного числа членов, например: 1+3+9+27+…
Дописывание
: 1/9+1/3+1+3+9+27+.. отбрасывание:
1+3+5+7+9+11
4)
Если
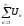 сходится
с суммойS
сходится
с суммойS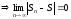 .
.
Общий вывод: на практике необязательно выяснять сходимость ряда по определению (вычисляя сумму S). Достаточно просто знать сходится этот ряд или расходится, поэтому, основное место в теории рядов занимают теоремы – признаки сходимости, которые позволяют исследовать ряд на сходимость, не вычисляя его суммы.
Признаки сходимости
Необходимый признак сходимости:
Если
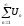 сходится,
то общий член
сходится,
то общий член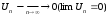
Доказательство:
Пусть
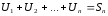 -n
– частичная сумма.
-n
– частичная сумма.
 -
число.
-
число.
При
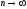 ,
,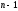 тоже
тоже и
и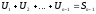 -n-1
– частичная сумма.
-n-1
– частичная сумма.
Она
имеет предел
 .
.
Т.к

 конец
доказательства.
конец
доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если
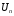 не
стремится к 0 при
не
стремится к 0 при

Примеры:
1)
2)

Числовые ряды с положительными членами
Рассмотрим
знакоположительный числовой ряд
 ,
где
,
где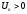 .Последовательность
частичных сумм такого ряда будет всегда
возрастающей:
.Последовательность
частичных сумм такого ряда будет всегда
возрастающей:

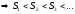
На 1 курсе была доказана теорема о том, что: монотонно возрастающая последовательность, ограниченная сверху имеет конечный предел.
 -
число.
-
число.
Для
знакоположительного ряда достаточно
доказать, что, последовательность
частичных сумм
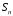 ограничена
сверху числом (возрастание и так есть).
ограничена
сверху числом (возрастание и так есть).
