2.3. Линейные дифференциальные уравнения второго порядка.

Линейным д.у. второго порядка называется уравнение вида

(2.6.)

где функции заданы на интервале.

При дляполучаем

(2.7)

Это линейное однородное уравнение второго порядка, соответствующее неоднородному уравнению (2.6).

Если - частные решения уравнения (2.7), то любая их линейная комбинация, где, является решением (2.7).

Определение. Две функции линейно независимы в интервале, если их отношение не является постоянной величиной, т.е.

Определение. Любая система из двух линейно независимых решений уравнения (2.7) называется фундаментальной системой решений (Ф.С.Р.) Пусть– фундаментальная система решений, тогда общее решение имеет структуру

(2.8)

гдеи- произвольные постоянные.

2.4. Линейные однородные уравнения с постоянными коэффициентами

Рассмотрим уравнение (2.7)

(2.9)

где .

Найдем решение д.у. (2.9) в виде , получаем. Т.к., то для нахождения решения выпишем квадратное уравнение, которое называется характеристическим для уравнения (2.9)

.

Пусть , т.е.– действительные и различные, тогда частные решения,будут составлять Ф.С.Р., и общее решение находим по формуле (2.8):

.

Если , т.е., то,составляют Ф.С.Р. и общее решение имеет вид

.

Если корни уравнения (2.9) являются комплексно сопряженными,и частные решения имеют вид

, .

Общее решение записывается по формуле (2.8):

.

Пример 1. Найти общее решение д.у. .

Решение: Составим характеристическое уравнение и найдем Ф.С.Р.

уравнения: ,.

Тогда общее решение: .

Ответ: .

Пример 2. Найти общее решение д.у. .

Решение: Составим характеристическое уравнение и найдем Ф.С.Р

уравнения: ,.

Тогда общее решение .

Ответ: .

Пример 3. Найти общее решение д.у. .

Решение: Составим характеристическое уравнение и найдем Ф.С.Р

уравнения: ,.

Тогда общее решение .

Ответ: .

2.5. Метод вариации произвольной постоянной

Рассмотрим уравнения

(2.10),

(2.11)

Общее решение неоднородного уравнения (2.10) находим по формуле

, (2.12)

где - общее решение однородного уравнения (2.11), а- частное решение неоднородного уравнения (2.10).

Пусть найдена фундаментальная система решений и общее решение соответствующего однородного д.у. (2.11). Тогда частное решениеуравнения (2.10) может быть найдено с помощью метода вариации произвольной постоянной (метод Лагранжа).

Сущность метода состоит в следующем. Частное решение неоднородного уравнения (2.10) ищется в виде (2.12), где заменены неизвестными функциями, т.е.

(2.13).

Можно доказать, что функции находятся из системы д.у.:

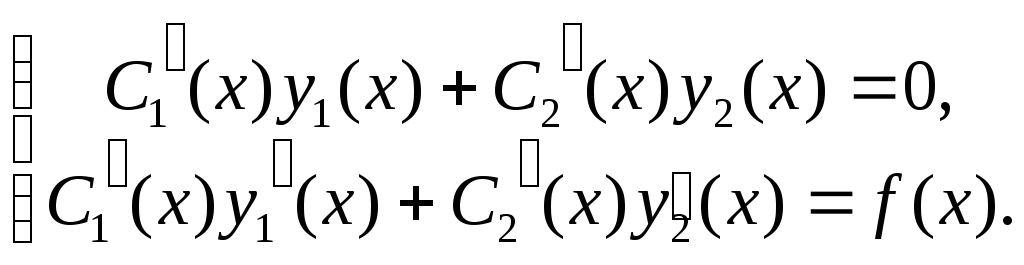(2.14)

Замечание: Системой (2.14) можно пользоваться, если коэффициент при в (2.10) тождественно равен единице. В противном случае уравнение нужно привести к указанному виду.

Система (2.14) имеет единственное решение

т.к. определитель системы не равен нулю при в силу линейной независимостии.

Пример 1.Найти общее решение дифференциального уравнения .

Решение: Решая характеристическое уравнение , находим.

Соответственно, общее решение линейного однородного д.у. имеет вид . Для нахождения частного решения

исходного дифференциального уравнения найдем из системы

Решая эту систему, находим . Интегрируя д.у. с разделяющимися переменными, получаем

,

и

.

Тогда общее решение исходного д.у. имеет вид

.

Ответ: .