11

Сигналы и линейные системы

Тема 12. Преобразование хартли

Ни одна вещь не возникает беспричинно, но все возникают на каком-нибудь основании и в силу необходимости.

Демокрит. Древне-греческий философ, атомистик, V-IV в. до н.э.

Следовательно, если что-то уже появилось, необходимо срочно найти для нее соответствующую необходимость. Иначе пропадет без принесения всякой пользы для человечества.

Григорий Старцев. Казахстанский геофизик Уральской школы, ХХ в.

Содержание

Введение.

1. Основные сведения. Определение преобразования. Связь преобразований Фурье и Хартли. Энергетический и фазовый спектры.

2. Свойства преобразования. Линейность. Четность и нечетность спектральных функций. Измерение аргумента функции. Теорема запаздывания. Преобразование производной. Преобразование интеграла. Преобразование свертки и произведения. Преобразование функции корреляции. Двумерное преобразование Хартли.

3. Дискретное преобразование Хартли. Формулы преобразования. Спектры числовых рядов. Свойства дискретного преобразования. Цифровая фильтрация методом свертки. Двумерная дискретная фильтрация.

Литература.

Введение

Преобразование Хартли является аналогом преобразования Фурье и может применяться для спектрального анализа, фильтрации и обработки сигналов. Название преобразование получило по имени Р.Хартли, опубликовавшего в 1942 г. статью о паре интегральных преобразований - прямом и обратном, использующих введенную им функцию cas  = cos  + sin . Преобразование оставались в забвении до 80-х годов прошлого века.

Обращение к преобразованию Хартли было обусловлено ситуацией, сложившейся в ряде методов обработки информации, использующих вещественные последовательности данных, обработку которых желательно осуществ­лять в области вещественных чисел. В отличие от преоб­разования Фурье, отображающего вещественные функции в ком­плексную область и несимметричного по комплексной переменной, пре­образование Хартли осуществляет преобразо­вания только в вещественной области, отображая вещественные сигналы s(t) в вещественные S(). Прямое и обратное преобразование Хартли взаимно сим­метричны. Большой вклад в развитие преобразования внес Р. Брейсуэлл, разработавший основы тео­рии непрерывного и дискретного преобразования Хартли, а также один из вариантов его быстрого преобразования. Применение преобразования перспективно для обработки изображений.

12.1. Основные сведения

Определение преобразования. Преобразование Хартли задается парой формул:

Sh() = (1/)s(t) cas t dt (12.1.1)

s(t) = (1/)Sh() cas t d (12.1.2)

где функция cas представляет собой сумму косинуса и синуса одного аргумента:

cas t = cos t + sin t. (12.1.3)

Множители 1/обусловлены применением в формулах аргумента . Они могут заменяться одним множителем 1/2 только в формуле (12.1.2), но это нарушает симметричность прямого и обратного преобразования. При необходимости применения симметричных алгоритмов в формулах можно использовать аргумент циклической частоты:

Sh(f) =s(t) cas 2ft dt (12.1.1')

s(t) =Sh(f) cas 2ft df (12.1.2')

На первый взгляд в формулах отсутствуют существенные отличия от интегральных преобразований Фурье, однако на практике эти различия могут быть достаточно ощутимыми, что определяется вещественным характером функции Sh(f).

Связь преобразований Фурье и Хартли. Допустим, имеется произвольная функция s(t) Sh(f), s(t) S(f), где Sh(f) и S(f) – результаты преобразования Хартли и Фурье (Хартли- и Фурье-образы s(t)). Любая функция y(x) может быть представлена в виде суммы четной и нечетной компонент, и однозначно по ним восстановлена. Четная компонента определяется как полусумма функции y(x) и ее зер­кального изображения y(-x), нечетная компонента определяется как полуразность этих функций и обладает свойством антисимметрии, т.е. y(-x) = -y(x). Запишем для преобразования Хартли:

Sh(f) =s(t) cas 2ft dt =s(t) cos 2ft dt + s(t) sin 2ft dt.

Sh(f) = Sh_sym(f) + Sh_asym(f),

Sh_sym(f) = [Sh(f)+Sh(-f)]/2 = s(t) cos 2ft dt, (12.1.4)

Sh_asym(f) = [Sh(f) - Sh(-f)]/2 = s(t) sin 2ft dt, (12.1.5)

где Sh_sym(f) и Sh_asym(f) – четная и нечетная компоненты Sh(f). C другой стороны, для преобразования Фурье имеем:

S(f) =s(t) exp(-2ft) dt = A(f) – j B(f).

A(f) =s(t) cos 2ft dt, - четная вещественная часть спектра,

B(f) =s(t) sin 2ft dt, - нечетная мнимая часть спектра.

Сравнивая эти две группы выражений, нетрудно сделать выводы по формулам связи преобразований Фурье и Хартли:

S(f) = Sh_sym(f) – j Sh_asym(f), (12.1.5)

Sh(f) = A(f) - B(f). (12.1.7)

Таким образом, преобразование Фурье равно разности четной составляющей пре­образования Хартли и нечетной составляющей, умноженной на j, а преобразование Хартли определяется как разность ве­щественной и мнимой составляющих преобразования Фурье.

Рис. 12.1.1.

Пример прямого и обратного преобразования Хартли для простого сигнала (гауссиан с быстро затухающей частотной характеристикой) и сопоставления четной и нечетной частей его спектра с действительной и мнимой частью спектра Фурье приведен на рис. 12.1.1.

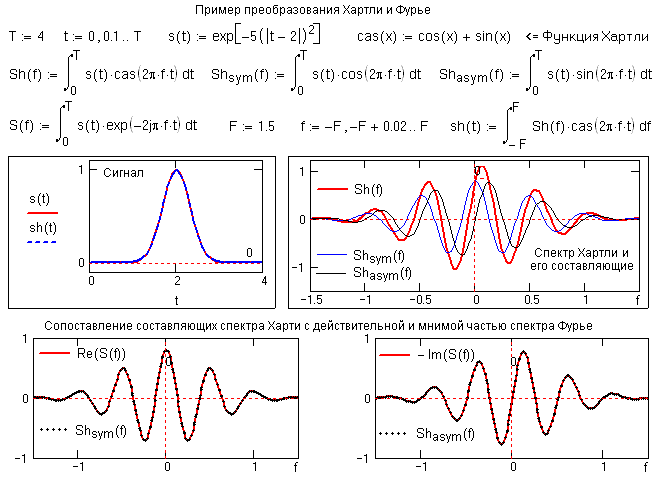
Как можно видеть на рисунке, спектр Хартли Sh(f) даже такого простого сигнала, как гауссиан, выглядит достаточно сложно, равно как и его четная и нечетная составляющие, и мало пригоден для визуального анализа. Отметим, однако, что действительная и мнимая части преобразования Фурье, хотя и имеют определенный физический смысл, как амплитудные распределения косинусных и синусных колебаний, в качественном анализе сигналов также используются достаточно редко. Гораздо большее практическое значение для анализа имеют модуль и фаза спектра (амплитудно-частотная и фазово-частотная характеристика) и спектр плотности мощности сигнала. Отметим также, что для преобразования Хартли не характерна избыточность преобразования Фурье, т.к. в общем случае вещественные функции Хартли эквивалентны сопряженным комплексным функциям Фурье.

Энергетический и фазовый спектры. Энергетический спектр преобразования Фурье (спектр плотности мощности сигнала) задается выражением:

W(f) = A²(f) + B²(f).

Частотный спектр плотности мощности сигнала не должен зависеть от формы математического представления спектра. Из этих соображений для вычисления энергетического спектра по спектру Хартли следует:

Wh(f) = (Sh_sym(f))² + (Sh_asym(f))² = [Sh(f)+Sh(-f)]²/4 + [Sh(f) - Sh(-f)]²/4,

Wh(f) = [Sh²(f)+Sh²(-f)]/2. (12.1.8)

Аналогично, вычисление фазовой частотной характеристики сигнала:

(f) = argtg(B(f)/A(f)) = argtg(-Sh_asym(f)/ Sh_sym(f)),

(f) = argtg(-[Sh(f) - Sh(-f)] / [Sh(f)+Sh(-f)]). (12.1.9)

Рис. 12.1.2.

На рис. 12.1.2. приведено продолжение вычислений для сигнала на рис. 12.1.1 и показаны частотные функции спектра плотности мощности и фазовой характеристики сигнала.

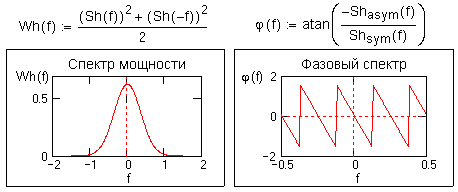
С учетом всех вышеприведенных выражений преобразование Хартли может рассмат­риваться как гладкая вещественная форма представления спектра вещественного сигнала.