
- •ЛЕКЦИЯ 5 МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ ГОРНЫХ АШИН
- •По характеру переменных, описывающих модель, различают модели фазовые и факторные.
- •Каждый участок в механической системе может одновременно обладать двумя или тремя названными свойствами.
- •Первое топологическое уравнение динамической системы есть уравнение равновесия
- •При малых значениях h члены, содержащие h во второй и более высоких степенях,
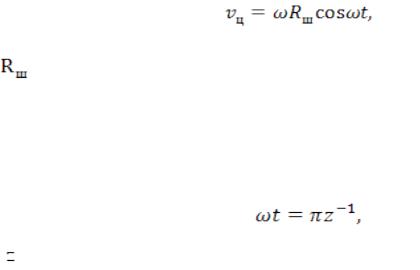
ЛЕКЦИЯ 5 МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ ГОРНЫХ АШИН
1. Моделирование внешних воздействий на трансмиссию горных машин
В горных машинах может быть несколько источников силовых и кинематических воздействий, которые определяют загруженность элементов трансмиссии.
Рабочие органы некоторых горных (в частности врубовых) машин выполнены в виде цепи с режущими элементами. Если цепь имеет относительно большую массу и жесткость или жестко связана с относительно большой массой, то, вследствие неравномерности ее движения, возникает сила инерции, направленная навстречу скорости цепи. При постоянной скорости вращения ведущей звездочки(1)ω скорость движения цепи зависит от угла поворота шарнира, находящегося на цепи:
где |
— радиус вращения шарнира цепи на звездочке, м. |
Ускорение цепи находится как первая производная скорости:
 (2)
(2)
Максимальное значение ускорения будет при
(3)
где |
— число зубьев ведущей звездочки. |
Соответственно максимальная сила инерции, действующая со стороны цепи на ведущую звездочку, записывается в виде
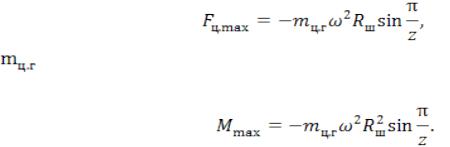
(4)
где — масса цепи и связанного с ней груза, кг.
Таким образом, приведенный к валу ведущей звездочки максимальный инерционный момент
(5)
Аналогичным образом моделируются внешние воздействия на ротор угольного комбайна, рабочий орган роторного экскаватора и рабочие органы других горных машин непрерывного2. Моделированиедействия. нагруженности динамических
систем горных машин при случайном нагружении
Нагрузки в узлах горных машин зависят от физико-механических свойств горных пород, скорости и траектории движения рабочего органа, параметров рабочего органа
идругих факторов. Большая часть этих факторов случайно изменяется в пространстве
ивремени, поэтому нагрузки в узлах горных машин также изменяются случайно.
Наиболее достоверный результат для анализа нагруженности узлов можно получить при тензометрировании нагрузок во время работы машины. Современная вычислительная техника дает возможность определять нагруженность новых проектируемых машин при помощи математических моделей, позволяющих имитировать случайные нагрузки на рабочем органе.
Состояние и поведение динамических систем горных машин можно охарактеризовать с
помощью фазовых переменных — скорости, силы, напряжения, деформации.
Математические модели этих систем получают при объединении компонентных и тТопологическиепологических уравненияий. — это уравнения связи элементов друг с другом. Они связывают однотипные фазовые переменные, которые относятся к взаимосвязанным элементам.

По характеру переменных, описывающих модель, различают модели фазовые и факторные.
Фазовые модели — это модели, в которых фигурируют фазовые переменные. Если предмет исследования — процессы функционирования объекта, т. е. фазовые
переменные рассматриваются как функции времени, то фазовые модели называют |
||
Факторная модель имеет вид |
|
|
имитационными моделями. |
(6) |
|
|
|
|
гдe |
— вектор внешних параметров; |
|
 — вектор выходных параметров объекта.
— вектор выходных параметров объекта.
В ряде случаев факторные модели можно получить в явной форме:
(7)
Такие модели (7) называются аналитическими.
При исследовании динамических систем основными простыми элементами являются:
—масса или момент инерции, отображающие свойства инерционности;
—упругое звено — пружина или торсион, отображающие свойства упругости;
—сопротивление, отображающее потери энергии на трение вязкое или сухое.
Величины, характеризующие простые элементы: |
или ; |
||||
m — масса, кг; J— момент инерции, |
|
; — жесткость, |
|||
— сопротивление, |
или |
|
. |
|
|
Фазовые переменные динамических систем: |
— скорость, |
; |
|||
— сила, Н; |
— момент кручения, |
; |
|||
—угловая скорость, рад/с;
—перемещение, м;
— угол поворота, рад.
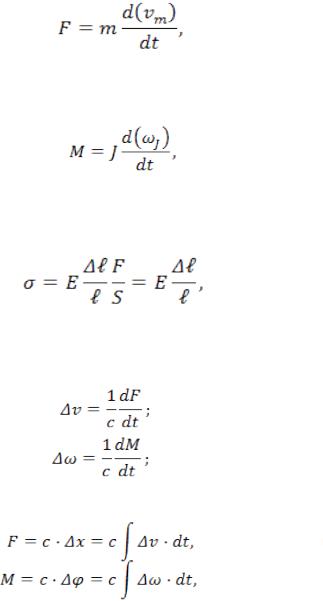
Каждый участок в механической системе может одновременно обладать двумя или тремя названными свойствами.
Компонентное уравнение массы получается из уравнения Лагранжа второго рода
(8)
где m — масса элементарного участка.
Аналогично для вращательного движения компонентное уравнение массы имеет вид
(9)
где J — момент инерции элементарного участка вала.
Компонентное уравнение упругого элемента получают из закона Гука:
(10)
где S — площадь поперечного сечения упругого элемента.
После дифференцирования уравнений (8) и (9) повремени получаются компонентные
уравнения упругого элемента: |
(11) |
|
(12)
В преобразованном виде эти компонентные уравнения имеют вид:
(13)
Первое топологическое уравнение динамической системы есть уравнение равновесия |
|
сил (14) или моментов для вращательной системы (15): |
(14) |
|
|
|
(15) |
Второе топологическое уравнение динамической системы выражает принцип сложения
скоростей и имеет вид |
(16) |
(17)
Объединяя компонентные уравнения элементов и топологические уравнения связей, получают математическую модель динамической системы.
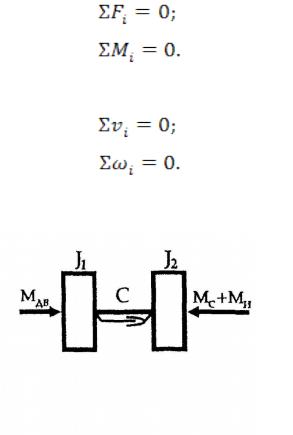
Рис. 1 Эквивалентная расчетная динамическая система
Рассмотрим процесс создания математической модели двухмассовой односвязной динамической системы, изображенной на рис. 1. Эта система разбивается на простые элементы:
— первая масса — двигатель, имеющий момент инерции J1 ;
— упругое звено — торсион (вал);
— вторая масса — рабочий орган, имеющийкомпонентныемоме инерции J .
Для каждого элемента записываются уравнения,2 а между ними топологические уравнения связей:
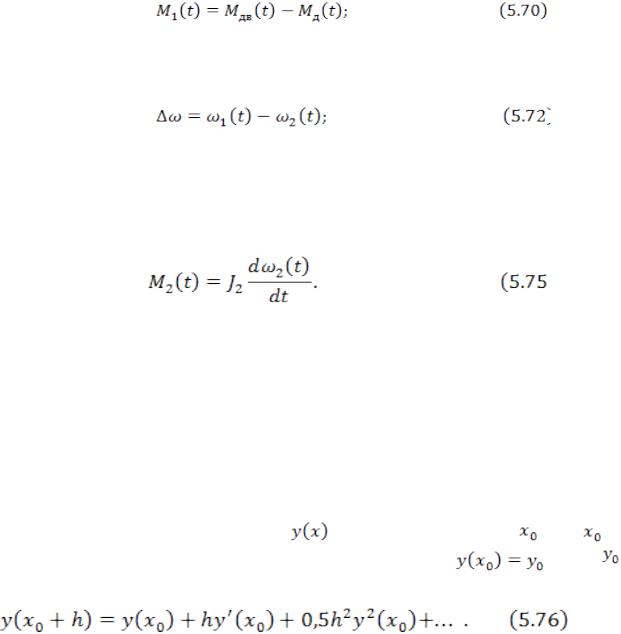
(17)  (18)
(18)
(19)  (21)
(21)
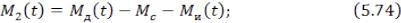 (22)
(22)
(23)
Для решения составленной имитационной модели могут быть использованы АВМ или ЦВМ.
Для решения этих дифференциальных уравнений необходимо знать значение зависимой переменной или ее производных при некоторых значениях независимой переменной. Если дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей Коши. Если условия задаются при двух и более значениях независимой переменной, то задача называется краевой. В задаче Коши дополнительные условия называются начальными, а в краевой —
граничными. В задачах Коши часто независимой переменной является время. В краевых |
||
Этот метод основан на разложении в ряд Тейлора функции |
в окрестностях точки |
|
задачах независимой переменной часто являются длина, угол. Решение уравнений |
||
(где |
— значение независимой переменной, при которой известно значение |
|
производится методом Эйлера. |
|
|
функции y: |
, т. е. есть начальное условие): |
|
(24)
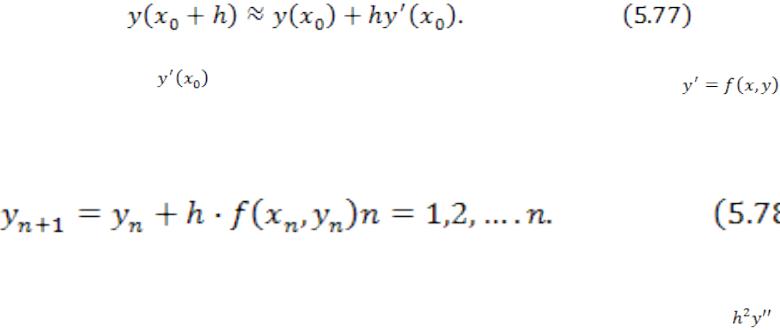
При малых значениях h члены, содержащие h во второй и более высоких степенях, могут быть отброшены, и тогда
|
(25) |
Значения первой производной |
находят при подстановке в исходное |
дифференциальное уравнение начального значения независимой переменной при малом смещении h от начальной точки. Этот процесс можно продолжить, используя соотношение
(26)
Ошибка при решении дифференциального уравнения методом Эйлера имеет порядок , так как члены, содержащие во второй и более высоких степенях, отбрасываются. Отсюда следует вывод: необходимо обоснованно назначать величину шага интегрирования. При моделировании динамических систем горных машин система, имеющая большую частоту собственных колебаний, должна иметь меньший шаг интегрирования по времени. Для решения дифференциальных уравнений второго порядка их приводят к уравнениям первого порядка.
