§ 3. Решение систем с параметром и с модулями

§ 4. Решение задач с помощью систем уравнений

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

M3_8_2010.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

364.31 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

10x −5y −3z = −9,

6x +4 y −5z = −1,3x −4 y −6z = −23.

Уравняем коэффициенты при x в первом и втором уравнениях, для этого умножим обе части первого уравнения на 6, а второго уравнения – на 10, получаем:

60x −30 y −18z = −54,60x +40 y −50z = −10.

Вычитаем из второго уравнения полученной системы первое урав-

нение, получаем: 70 y −32z = 44, 35y −16z = 22.

Из второго уравнения исходной системы вычитаем третье уравнение, умноженное на 2, получаем: 4 y +8y −5z +12z = −1+46,

12 y +7z = 45.

Теперь решаем новую систему уравнений:

35y −16z = 22,12 y +7z = 45.

К первому уравнению новой системы, умноженному на 7, прибавляем второе уравнение, умноженное на 16, получаем:

35 7 y +12 16y = 22 7 +45 16,

245y +192y =154 +720, 437 y =874,	y = 2. Подставляем y = 2 в
уравнение 12 y +7z = 45, получаем:	24 +7z = 45, 7z = 21, z =3.

Теперь подставляем y = 2, z =3 в первое уравнение исходной сис-

темы, получаем: 10x −5 2 −3 3 = −9, 10x −10 −9 = −9, 10x =10, x =1.

Ответ: (1; 2;3). ▲

ax +4 y = 2a,

Рассмотрим систему уравнений

x +ay = a.

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

В этой системе, на самом деле, три переменные, а именно: a, x, y. Неизвестными считают x и y, a называют параметром. Требуется найти решения (x, y) данной системы при каждом значении параметра a.

Покажем, как решают такие системы. Выразим переменную x из второго уравнения системы: x = a −ay. Подставляем это значение для x в первое уравнение системы, получаем:

a (a −ay)+4y = 2a,

(2 −a)(2 +a)y = a (2 −a).

Если a = 2, то получаем уравнение 0 y = 0. Этому уравнению удовлетворяет любое число y, и тогда x = 2 −2 y, т. е. при a = 2 пара чисел (2 −2 y; y) является решением системы. Так как y может быть

любым числом, то система при a = 2 имеет бесконечно много решений.

Если a = −2, то получаем уравнение 0 y =8. Это уравнение не имеет ни одного решения.

Если теперь a ≠ ±2,				то y =		a (2 −a)	=	a	,
						(2 −a)(2 +a)		2 +a
x = a −ay = a −	a2		=	2a	.
	2	+a		2 +a

Ответ: При a = 2 система имеет бесконечно много решений вида (2 −2 y; y), где y − любое число;

Мы решили эту систему и установили, при каких значениях параметра a система имеет одно решение, когда имеет бесконечно много решений и при каких значениях параметра a она не имеет решений.

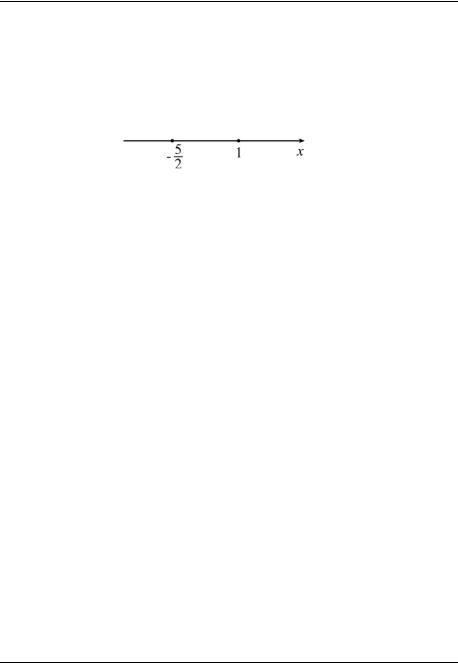
Пример 1. Решите систему уравнений

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

−3

y −1

=3,

3x −2 y =5.

Из второго уравнения системы выражаем x через y, получаем

x =

2 y +5

подставляем это значение для x в первое уравнение сис-

темы, получаем:												2			2y +5				−3		y −1			=3;						4		y	+		5						−3				y		−1				=3.
												2																		4					5
											3																	3							2
											3					5 =0												3				5			2																			5 ,
		Выражение											y +			5 =0					при					y = −						5	.						Если											y > −				5 ,			то
																2																2																						2
	y +		5	= y +				5		; если						y <		−5		,	то		y +			5			= −y				−			5			.
			5					5																		5										5
							2																												2
	2						2											2						2											2
		Выражение y −1 =0,																если y =1. Если														y >1, то														y −1						= y −1, а ес-
		Выражение y −1 =0,																если y =1. Если														y >1, то														y −1						= y −1, а ес-
ли y <1, то									y −1					=1− y.													5		= y +					5			,
ли y <1, то									y −1					=1− y.

		Если y ≥1, то													y −1		= y −1 и							y +																		получаем уравнение:


	4				5													4						2									2
																								2									2
						−3(y					−1)=3,											10																					5									10
		y +																		y	+			−3y				+3 =					3, −													y	= −						,	y =			2.
		y +																3		y	+	3		−3y				+3 =					3, −										3			y	= −					3	,	y =			2.
	3				2													3				3																					3									3
Тогда				x =		1	(2 2 +								5)=3. Число 2 >1, так что пара (3;2) является ре-
						3
шением системы.
		Пусть теперь										−			5 ≤ y <1,						тогда				y −1						=1		− y;											y +					5			= y +			5	.	Для



														2																																	2							2
														2																																	2							2
																																						4										5
нахождения										y					получаем								уравнение																			y				+						+3y −3					=3,
нахождения										y					получаем								уравнение																			y				+						+3y −3					=3,
																																						3										2
												4 y +10						+3y = 6,						13 y = 8								, y =									8			;
												4 y +10						+3y = 6,						13 y = 8								, y =												;
											3					3								3				3												13

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

									x =		1	(2 y +5)=		1	16				27
																+5	=				.
											3			3		+5	=		13		.
											3			3	13				13
Число						8	больше				−	5	, но меньше, чем						1,		поэтому пара чисел

						13
						13						2
	27		;		8		является решением системы.

	13
	13			13
								5												4		5
		Если					y < −		,	то получаем уравнение:								−			y +		+3y −3	=3,
		Если					y < −	2	,	то получаем уравнение:								−		3	y +		+3y −3	=3,
								2												3		2
−	4 y −					10	+3y =6,			5 y =			28 , y = 28 .			Это		значение					больше,	чем
	3					3				3			3		5
	−	5			,	поэтому решений нет.


		2

Таким образом, система имеет два решения (3;2) и 1327 ;138 . ▲

при a = −2 система не имеет решений;

при a ≠ ±2, система имеет единственное решение

Пример 1. Путь от города до посёлка автомобиль проезжает за 2,5 часа. Если он увеличит скорость на 20 км/ч, то за 2 часа он пройдёт путь на 15 км больший, чем расстояние от города до посёлка. Найдите это расстояние.

Обозначим через S расстояние между городом и посёлком и через V скорость автомобиля. Тогда для нахождения S получаем систему из двух уравнений

2,5V = S,

(V + 20)2 = S +15.

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

Из первого уравнения V =	S	=	2	S, подставляем это значение V

2,5		5

Ответ: 125 км. ▲

Пример 2. Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 больше исходного. Найдите эти числа.

Пусть данное число ab, т.е. число десятков равно a, а число единиц равно b. Из первого условия задачи имеем: a + b =15. Если из числа ba вычесть число ab, то получится 27, отсюда получаем второе уравнение: 10b + a −(10a + b)= 27.

Решаем систему уравнений

a + b =15,

−9a + 9b = 27,

a + b =15,

a −b = −3.

Сложим уравнения последней системы, получаем: 2a =12, a = 6, тогда b = 9. Заданное число 69, второе число 96.

Ответ: 69 и 96. ▲

Пример 3. Имеется сталь двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять каждого из этих сортов стали, чтобы получилось 140 т стали с содержанием никеля 30%?

	Обозначим через x массу стали с 5% содержанием никеля и через
y	массу стали с 40% содержанием никеля. Тогда x + y =140. В
x	тоннах стали содержится 0,05x никеля, а в y тоннах стали содер-

жится 0, 4 y никеля. Масса никеля равна 0, 05x + 0, 4 y и составляет

30% от140 т, т.е. 3 140 т = 42 т. Получили второе уравнение

0,05x + 0, 4 y = 42.

2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.

Умножим обе части уравнения на 20, получим: x +8y = 840. Для нахождения x и y получили систему уравнений


	x + y =140,
	x +8 y = 840.
Вычтем	из второго уравнения первое уравнение, получим:
7 y = 700,	y =100, тогда x =140 − y = 40.

Ответ: 40 т, 100 т. ▲

Пример 4. Оператор ЭВМ, работая с учеником, обрабатывает задачу за 2 ч 24 мин. Если оператор будет работать 2 ч, а ученик 1 ч, то бу-

дет выполнено 23 всей работы. Сколько времени потребуется операто-

ру и ученику в отдельности на обработку задачи?

Обозначим всю работу за 1, производительность оператора за x и производительность ученика за y. Учитываем, что

2 ч24 мин=2 52 ч=125 ч.

Из первого условия задачи следует, что (x+y)125 =1. Из второго условия задачи следует, что 2x + y = 23 . Получили систему уравнений

										(x+y)				12	=1,
										(x+y)				5	=1,
														5
																2
										2x + y =						2		.
										2x + y =					3			.
															3
Решаем эту систему методом подстановки:
y =	2	− 2x;				2			12				2				12				12			8
			x+			3	−2x			=1;			3	−x					=1;				x =		−1;
	3		x+				−2x			=1;				−x			5		=1;		5		x =	5	−1;
	3								5								5				5			5
				12	x =			3	; x =		1	; y =			2			−	1	=	1	.
				5			5			4					3				2		6

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.06.2015688.23 Кб78M1_10_14.pdf
#
03.06.2015504.99 Кб117M1_11_2012.pdf
#
03.06.2015581.89 Кб46M1_8_14.pdf
#
03.06.2015849.06 Кб71M3_10_14.pdf
#
03.06.2015603.08 Кб50M3_8_14.pdf
#
03.06.2015364.31 Кб62M3_8_2010.pdf
#
03.06.2015654.44 Кб54M4_10_14.pdf
#
27.03.2016653.19 Кб72M4_10_15.pdf
#
03.06.2015441.25 Кб64M4_8_2010.pdf
#
03.06.2015463.11 Кб75M5_8_2010.pdf
#
27.03.2016117.26 Кб9ma1^.pdf