
Tree ++++
.pdfАлгоритм однократной балансировки
Если после вставки показатели сбалансированности вершин имеют одинаковый знак и отличаются только на единицу, то восстановить баланс дерева можно однократным поворотом, включая одно "переприкрепление" поддерева), при этом вставка не будет оказывать влияния на другие участки дерева.
61
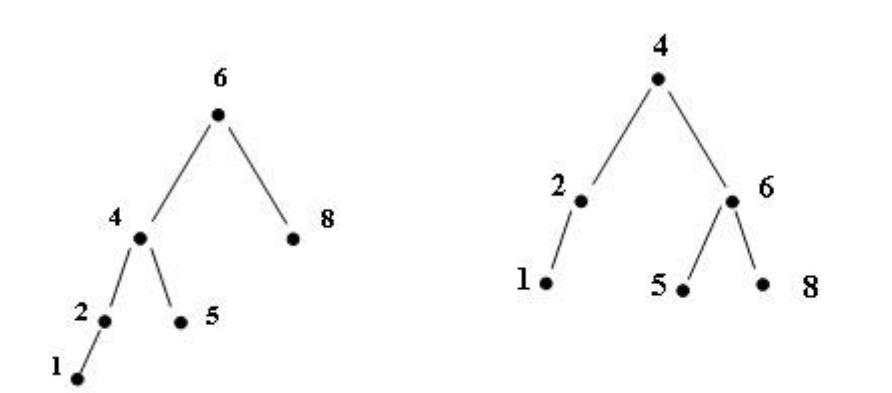
Пример балансировки
До балансировки |
После балансировки |
62
Алгоритм LL балансировки
1.Определяем адрес той вершины, которая станет корнем дерева: q = p->Left;
2.Перекрепляем правое поддерево от "нового" корня, делая это поддерево левым поддеревом "старого" корня:
p->Left =q->Right;
3.Определяем правое поддерево "нового" корня, как начинающееся со "старого" корня: q->Right = p;
4.Изменяем значение указателя на корень дерева (p) и обнуляем значение сбалансированности:
p->bal = 0; p = q;
63
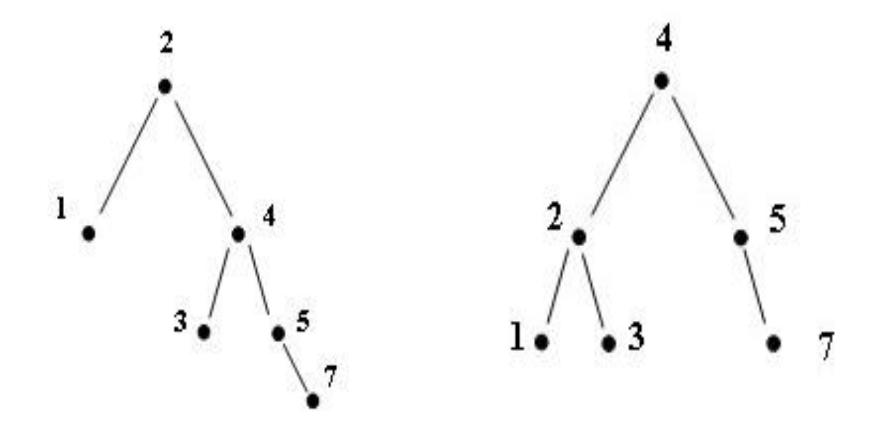
Алгоритмы балансировки. Однократный RR-поворот
До балансировки |
После балансировки |
64
Алгоритм RR балансировки
1.Определяем адрес той вершины, которая станет корнем дерева: q = p-> Right;
2.Открепляем левое поддерево от "нового" корня, делая это поддерево правым поддеревом "старого" корня: p-> Right = q-> Left ;
3.Определяем левое поддерево "нового" корня, как начинающееся со "старого" корня: q-> Left = p;
4.Изменяем значение указателя на корень дерева (p) и обнуляем значение сбалансированности:
p->bal = 0; p = q;
65
Алгоритм балансировки. Двукратный LR-поворот
L = p-> Left; R = L-> Right; L->Right = R-> Left; R->Left = L; p-> Left = R-> Right; R-> Right = p; p = R;
66
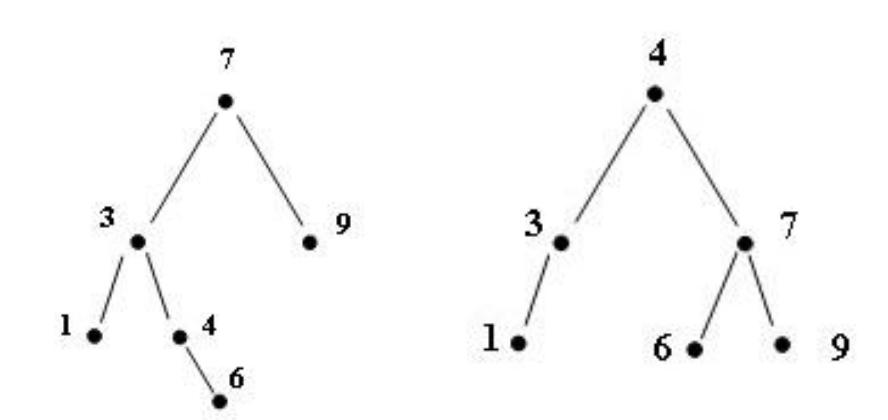
Пример балансировки. Двукратный LR-поворот
До балансировки |
После балансировки |
67
Алгоритм LR балансировки
1. Определим L как указатель на левое поддерево p, а R как указатель на правое поддерево дерева L: L = p->Left; R = L->Right;
2.Открепляем левое поддерево дерева R и прикрепляем его на место правого поддерева дерева L: L->Right = R->Left;
3.Определяем левое поддерево "нового" корня R, как начинающееся с L: R->Left = L;
4.Определяем левое поддерево "нового" корня R, как начинающееся с L: R->Left = L;
5.Открепляем правое поддерево дерева R прикрепляем его на место левого поддерева "старого" корня: p->Left =R->Right;
6.Определяем правое поддерево "нового" корня R, как начинающееся со "старого" корня: R->Right = p;
7.Изменяем значение указателя на корень дерева p: p = R;
68
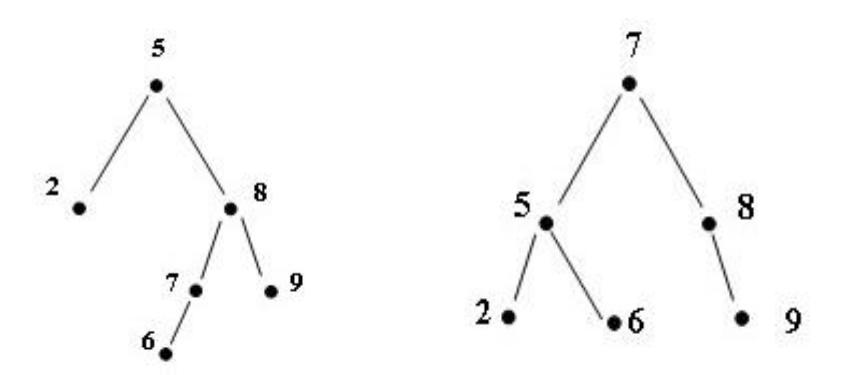
Пример балансировки. Двукратный RL-поворот
До балансировки |
После балансировки |
R =p->Right; L = R->Left; R->Left = L-> Right; L-> Right = R; p-> Right = L-> Left; L-> Left = p;
p = L; |
69 |
|
Алгоритм RL балансировки
1. Определим L как указатель на правое поддерево p, а R как указатель на левое поддерево дерева L: L = p->Right; R = L->Left;
2.Открепляем правое поддерево дерева R и прикрепляем его на место левого поддерева дерева L: L->Left = R-> Right;
3.Определяем правое поддерево "нового" корня R, как начинающееся с L: R-> Right = L;
4.Определяем левое поддерево "нового" корня R, как начинающееся с L: R->Left = L;
5.Открепляем левое поддерево дерева R и прикрепляем его на место правого поддерева "старого" корня: p-> Right =R->Left;
6.Определяем правое поддерево "нового" корня R, как начинающееся со "старого" корня: R->Left = p;
7.Изменяем значение указателя на корень дерева p: p = R;
70
