Иванова. Построение графиков функции

Функция неотрицательна и f 6 f 4 0, а в других

точках положительна, поэтому x 4, и x 6 — точки локального минимума. Без дополнительного исследования с помощью производной или представления функции формулой Тейлора в окрестности этих точек мы не можем для иррациональной функции описать ее поведение в окрестности точек минимума. Поэтому на эскизе (рис. 11.1) мы опускаем малые окрестности этих точек.

Найдем первую и вторую производные

f x 2 x 6 x 4 x 6 2 sign x 4

3 x 6 4 x 42

33

34

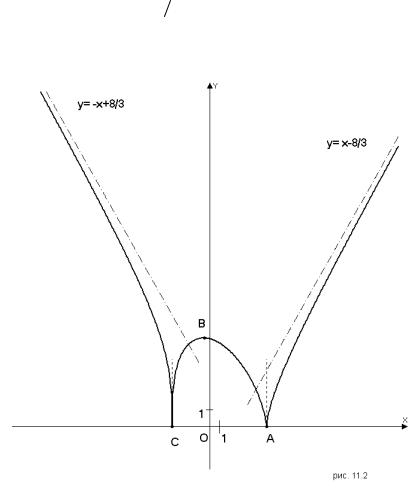
График функции изображен на рис. 11.2.

◄

35

Пример 5. Исследовать функцию f x x 4 3 1 9 и по- x

строить ее график.

► Область определения функции Dy ;0 0; .

Асимптоты.

то прямая x 0 — вертикальная асимптота.

Наклонные асимптоты для иррациональной функции находим методом выделения главной части.

причем график лежит ниже асимптоты. Аналогично из равенства

является асимптотой графика функции при x , причем график функции лежит ниже асимптоты, так как x 0.

В достаточно малой правой окрестности нуля функция стремиться к , можно предположить, что функция выпукла вниз. В достаточно малой левой окрестности нуля функция стремится к вертикальной асимптоте на , можно предположить, что функция выпукла вверх. При положительных аргументах функция положительна, если x 4. Исследование поведения иррациональной

36

функции в окрестности точки минимума проведем позднее с помощью производной. На эскизе этот участок не отражаем. Строим эскиз (рис. 12.1).

функции различно.

37

38

39

2 и построить ее график.

x 1

►Область определения функции Dy ;1 1; .

Асимптоты.

вертикальная асимптота, при чем функция стремится к ней слева. Наклонные асимптоты для иррациональной функции находим методом выделения главной части, для определения взаимного расположения графика и асимптоты представим функцию фор-

1

мулой Тейлора до o при x . Имеем

x

является асимптотой графика функции при x ,

график лежит выше асимптоты. Аналогично прямая y x 2 является асимптотой графика функции при x , причем график лежит ниже асимптоты, так как x 0.

Строим эскиз (рис. 13.1).

40

Найдем первую и вторую производные

41

Так как поведение функции в окрестности точки x 1 трудно изобразить на основном рисунке, сделаем выносной рисунок (рис. 13.2). График функции изображен на рис. 13.3.

42