
Иванова. Построение графиков функции
.pdfСодержание |
|
Построение графиков функций . . . . . . . . . . . . |
5 |
1. План исследования функции при построении графика . . |
5 |
2. Основные понятия и этапы исследования функции . . . . |
5 |
1. Область определения функции Df и множество |
|
значений функции Ef . Специальные свойства |
|
функции . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
2. Исследование асимптот . . . . . . . . . . . . . . . . . |
6 |
2.1. Вертикальные асимптоты . . . . . . . . . . . . . . . |
6 |
2.2. Наклонные (горизонтальные) асимптоты . . . . . . . |
6 |
2.3. Методы исследования невертикальных асимптот . . |
6 |
2.4. Взаимное расположение графика функции |
9 |
и его асимптоты . . . . . . . . . . . . . . . . . . . . . . . |
|
3. Построение эскиза графика функции . . . . . . . . . . |
11 |
4. Участки возрастания и убывания функции |
|
Точки минимума и максимума . . . . . . . . . . . . . . . |
11 |
5. Выпуклость функции вверх и вниз |
14 |
Точки перегиба . . . . . . . . . . . . . . . . . . . . . . . |
|
3. Дифференцирование функции, аналитическое |
|
выражение которой содержит модуль . . . . . . . . . . . . . |
17 |
4. Основные требования к результатам исследования |
|
и построению графика . . . . . . . . . . . . . . . . . . . . . |
18 |
5. Примеры исследования функций и построения |
20 |
графиков функций . . . . . . . . . . . . . . . . . . . . . . . |
|
Пример 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
20 |
Пример 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
24 |
Пример 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
29 |
Пример 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
Пример 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
36 |
Пример 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
40 |
Построение кривых . . . . . . . . . . . . . . . . . . . . |
44 |
1.План исследования и построения кривых . . . . . . . . . . |
44 |
3
2. Основные понятия и этапы исследования кривой . . . . . |
44 |
|
1. |
Исследование функций x x t и y y t . . . . . . . |
44 |
2. |
Использование результатов исследования x x t . . |
45 |
2.1. Вертикальные асимптоты кривой . . . . . . . . . . . |
45 |
|
2.2. Наклонные (горизонтальные) асимптоты кривой . . |
45 |
|
3. |
Анализ результатов и построение эскиза |
46 |
графика функции . . . . . . . . . . . . . . . . . . . . . . |
||
4. Участки возрастания и убывания кривой |
|
|
Точки минимума и максимума функций |
|
|
x x y и y y x , точки возврата кривой . . . . . . . |
46 |
|
5. |
Выпуклость функции вверх и вниз. Точки перегиба . . |
48 |
3. Построение параметрически заданных кривых . . . . . . |
49 |
|
Пример 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
49 |
|
Пример 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
54 |
|
Пример 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
58 |
|
Задачи для самостоятельного решения . . . . . . |
63 |
|
Ответы . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
66 |
|
4
Построение графиков функций
1.План исследования функции при построении графика
1.Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции: четность, нечетность; периодичность, свойства симметрии.
2.Исследовать асимптоты графика функции: вертикальные, наклонные. Проанализировать взаимное расположение графика функции и его наклонных (горизонтальных) асимптот.
3.Построить эскиз графика.
4.Найти участки монотонности функции: возрастание и убывание. Найти экстремумы функции: минимумы и максимумы.
Найти односторонние производные в точках разрыва производной функции и в граничных точках области определения функции (если односторонние производные существуют).
5.Найти промежутки выпуклости функции и точки перегиба.
2.Основные понятия и этапы исследования функции
1. Область определения функции Df и множество значе-
ний функции E f . Специальные свойства функции
Указать область определения функции, на оси абсцисс отметить ее граничными точками и выколотыми точками, указать абсциссы этих точек. Нахождение области определения функции приводить не обязательно.
Множество значений функции находить не обязательно. Легко исследуемые свойства множества значений: неотрицательность, ограниченность снизу или сверху и т.п., используются для построения эскиза графика, контроля результатов исследования и правильности построения графика.
5

График четной функции симметричен относительно оси ординат Oy . График нечетной функции симметричен относительно начала координат. Четные и нечетные функции исследуют на положительной половине области определения.
Периодическую функцию исследуют на одном периоде, а
график приводят на 2-3-х периодах. |
|
|
|
|
|
|||||
2. Исследование асимптот |
|
|
|
|
|
|
||||
2.1. Вертикальные асимптоты |
|
|
|
|
|
|||||
Определение 1. |
Прямая |
x x0 |
называется |
вертикальной |
||||||
асимптотой графика функции |
y f x , |
если выполнено |
хотя |
|||||||
бы одно из условий: |
lim f x 1 |
или |
lim f x . |
|
||||||
|
|
|
|
x x0 0 |
|
|
|
x x0 0 |
|
|
2.2. Наклонные (горизонтальные) асимптоты |
|
|
||||||||
Определение 2. Прямая y kx b называется (невертикаль- |
||||||||||
ной) асимптотой графика функции |
y f x приx , |
если |
||||||||
lim f x kx b 0. |
|
|
|
|
|
|
||||
x |
|
|
|
|
|
при x |
|
|
||
Из |
определения асимптоты |
следует, |
что |
|||||||
k lim |
f x |
, |
b lim f x kx . Вычисляя соответствующие |
|||||||
|
||||||||||
x |
x |
|
x |
|
|
|
|
|
|
|
пределы, получаем уравнение асимптоты y kx b . |
|
|||||||||
Аналогичное утверждение справедливо и в случае, когда |
||||||||||
x . |
|
|
|
|
|
|
|
|
||
Если k 0, то асимптота называется наклонной. |
Если |
|||||||||
k 0, то асимптота |
y b называется горизонтальной. |
|
||||||||
Аналогично вводятся понятия наклонной и горизонтальной |
||||||||||
асимптоты графика функции y f x |
при x . |
|
||||||||
2.3. Методы исследования невертикальных асимптот Исследование асимптот при x и при
правило проводят отдельно.
1Символ мы будем использовать, подразумевая выполнение одного случая, либо
, либо .
6

В некоторых частных случаях возможно совместное исследование асимптот при x и при x , например, для
1)рациональных функций;
2)четных и нечетных функций, для графиков которых исследование можно проводить на части области определения.
Метод выделения главной части. Для нахождения асимптоты выделяем главную часть функции при x . Аналогично при x .
Главную часть дробно рациональной функции удобно находить, выделяя целую часть дроби:
Пример 1. Найти наклонные асимптоты графика функции
2
f x 2x 3x 2 . x 1
► f x 2x 5 |
3 |
|
. Так как |
3 |
o 1 при |
x , то пря- |
|
x 1 |
|
x 1 |
|
||
мая y 2x 5 является искомой асимптотой. ◄
Главную часть иррациональной функции при решении практических примеров удобно находить используя методы представления функции формулой Тейлора при x .
Пример 2. Найти наклонную асимптоту графика функции
f x |
|
x4 3x 1 |
|
при x . |
|
|
|
|
|||||||||||
|
|
x 4 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
►Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
4 1 |
|
4 |
1 |
|
|||||
|
|
|
|
3 |
|
1 |
|
|
|||||||||||
f x x |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
x 1 |
|
o |
|
x 4 o1 |
||
|
3 |
|
|
4 |
|
|
|
|
|||||||||||
|
|
|
|
x |
|
x |
|
|
|
x |
|
x |
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
при x , то прямая |
y x 4является искомой асимптотой. |
|||||||
◄ |
|
|
|
|
|
|
|
|
Главную |
часть |
иррациональных |
функций |
вида |
||||
f x |
|
|
f x 3 |
|
удобно нахо- |
|||
ax2 bx c и |
ax3 bx2 cx d |
|||||||
дить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.
7

Пример 3. Найти наклонные асимптоты графика функции f x 
 x2 6x 14 при x и x .
x2 6x 14 при x и x .
►В подкоренном выражении выделим полный квадрат
f x |
x 3 2 |
5. Так как график функции |
f x симметричен |
||||||||||||||||
относительно прямой x 3 и |
f x |
|
x 3 |
|
|
|
5 |
|
|
|
|
|
, |
||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||||
то f x ~ |
|
x 3 |
|
|
при x . |
|
|
|
|
|
|
x 3 2 5 |
|
x 3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Значит, прямая |
y x 3 является |
|||||||||||||||
|
|
||||||||||||||||||
асимптотой при x , а прямая y 3 x |
— асимптотой при |
||||||||||||||||||
x . ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для нахождения асимптот можно использовать метод выделения главной части.
Пример 4. Найти асимптоты графика функции f x 
 4x2 x 2 .
4x2 x 2 .
►Так как
f x 2 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
1 |
|
|
|
|
|
2 |
|
x |
|
1 |
|
|
|
|
o |
|
, то функция |
|||
|
|
|
2 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
4x |
|
2x |
|
|
|
|
|
8x |
|
4x |
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
имеет асимптоту |
|
y 2x |
1 |
|
при |
x |
и асимптоту |
|||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||
y 2x |
при x .◄ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для трансцендентных функций приемлемы оба метода ис- |
||||||||||||||||||||||
следования асимптот при решении практических примеров. |
||||||||||||||||||||||
Замечание 1. При исследовании асимптот иррациональных, трансцендентных функций, а также функций, аналитическое выражение которых содержит модуль, целесообразно рассматривать два случая: x и x . Совместное исследование асимптот при x и при x может привести к ошибкам в исследовании. При нахождении пределов или главной части при x необходимо выполнить замену переменной x t .
8
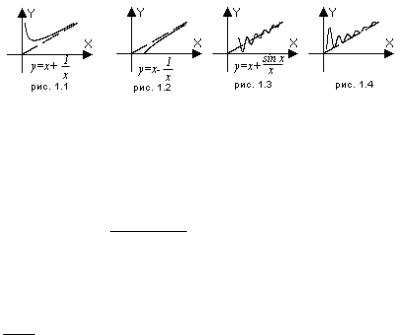
2.4. Взаимное расположение графика функции и его асимптоты
а) Если функция y f x имеет асимптоту при x ,
дифференцируема и строго выпукла вниз на луче x x0, то гра-
фик функции лежит выше асимптоты (рис. 1.1).
б) Если функция y f x имеет асимптоту при x ,
дифференцируема и строго выпукла вверх на луче x x0, то
график функции лежит ниже асимптоты (рис. 1.2).
в) Могут быть другие случаи поведения графика функции при стремлении к асимптоте. Например, возможно, что, график функции бесконечное число раз пересекает асимптоту (рис. 1.3 и 1.4).
Аналогичное утверждение справедливо и при x .
До исследования свойств выпуклости графика функции взаимное расположения графика функции и его асимптоты можно определить по знаку o 1 в методе выделения главной части.
Пример 5. Определить взаимное расположение графика
функции f x 2x2 3x 2 и его асимптот. x 1
► f x 2x 5 |
3 |
|
. Так как |
3 |
0 |
при x , то гра- |
x 1 |
|
|||||
|
|
x 1 |
y 2x 5. Так как |
|||
фик функции лежит |
выше асимптоты |
|||||
3
0 при x , то график функции лежит ниже асимпто-
x1
ты y 2x 5. ◄
9

Пример 6. Определить взаимное расположение графика
функции f x |
|
x4 3x 1 |
и его асимптоты при x . |
|||||||||||||
|
x 4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
8 |
|
1 |
|
|
|
1 |
1 |
|
|||
|
|
f x |
|
x |
x |
4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||
►Из равенства |
|
|
|
|
|
x 4 |
|
o |
|
при |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
|
|
|
|
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||
x следует, что график функции лежит ниже асимптоты y x 4. ◄
Пример 7. Определить взаимное расположение графика функции f x 
 x2 6x 14 и его асимптот.
x2 6x 14 и его асимптот.
5
► Так как f x x 3  (см. пример 3), то
(см. пример 3), то
x 3 2 5 x 3
график функции лежит выше асимптоты y x 3 при x и при x . ◄
Пример 8. Определить взаимное расположение графика
функции |
f x 3 x3 6x2 2x 14 и его асимптот. |
|
|
|
||||||||||||||||||||||||
► Так |
как x3 6x2 |
2x 14 x 2 3 14x 6, то применяя |
||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
a b |
|
|
|
|||||||||
формулу |
a |
|
b |
|
|
|
|
|
|
при |
||||||||||||||||||
|
|
3 |
|
|
|
2 |
3 |
|
3 |
|
3 |
|
|
2 |
|
|
||||||||||||
|
|
a |
a |
b |
b |
|||||||||||||||||||||||
a x 2 3 14x 6, |
b x 2 3 , получаем f x x 2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
14x 6 |
|
|
|
|
|
|
|
|
|
. |
Эта |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 x 2 3 14x 6 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x 2 3 |
x 2 3 14x 6 |
x 2 2 |
|
|
|
||||||||||||||||||||||
разность положительна при x |
3 |
|
и отрицательна при x |
3 |
. |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|||||||
Поэтому при x график функции лежит ниже асимптоты y x 2, а при x — выше асимптоты y x 2.◄
10

Метод вычисления пределов для исследования асимптот не позволяет оценить взаимное расположение графика функции и его асимптоты.
3. Построение эскиза графика функции Для построения эскиза графика отмечаются вертикальные и
наклонные асимптоты, точки пересечения графика функции с осями. Учитывая взаимное расположение графика функции и асимптот, строится эскиз графика. Если график функции лежит выше (ниже) асимптоты при x , то, предполагая, что суще-
ствует такая точка x0 , что среди точек x x0 нет точек перегиба,
получаем, что функция выпукла вниз(вверх), то есть к асимптоте. Аналогично можно прогнозировать направление выпуклости к асимптоте для вертикальных асимптот и для асимптоты при x . Однако, как показывает приведенный выше пример
функции y x sin2 x , такие предположения могут быть не x
верны.
4. Участки возрастания и убывания функции. Точки минимума и максимума
Определение 3. |
Функция f x называется |
возрастающей |
(убывающей) на интервале a,b , если для любых |
x1,x2 a,b , |
|
таких что x1 x2 |
имеет место неравенство |
f x1 f x2 |
( f x1 f x2 ). |
|
|
Дифференцируемая на интервале a,b функция f x воз-
растает (убывает) на интервале a,b , тогда и только тогда, когда
для любого x a,b |
|
|
f x 0 ( f |
x 0). |
Определение 4. Точка x0 называется точкой строгого ло-
кального максимума (минимума) функции f x , если:
1) функция определена в некоторой окрестности точки x0 ;
11

2) существует окрестность U x0 Df , такая что для лю-
бого |
x U x |
справедливо неравенство |
f x f x |
0 |
|
|
0 |
|
|
|
( f x f x0 ).
Точки минимума и максимума называются точками экстре-
мума функции f x . |
|
|
Необходимое условие экстремума. Если |
x0 |
— точка экс- |
тремума функции f x , то в этой точке либо |
f x0 0, либо |
|
производная не существует. |
|
|
Достаточные условия экстремума. |
|
f x диффе- |
1. Пусть существует 0, такое что функция |
||
ренцируема в проколотой -окрестности точки x0 |
и непрерывна |
|
в точке x0 . Тогда, |
|
|
а) если ее производная меняет знак минус на плюс при пере-
ходе через точку |
x0 , |
|
|
т.е. f x 0 для любого x x0 ,x0 , |
|||
f |
|
|
x x0,x0 , то x0 — точка максимума |
x 0 для любого |
|||
функции f x ; |
|
|
|
|
б) если ее производная меняет знак плюс на минус при пере- |
||
ходе через точку |
x0 , |
|
|
т.е. f x 0 для любого x x0 ,x0 , |
|||
f |
|
|
x x0,x0 , то x0 — точка минимума |
x 0 для любого |
|||
функции f x .
Модельными примерами могут служить y x (рис. 2.1) и
y x (рис.2.2).
12
