Иванова. Построение графиков функции

23

Асимптоты.

Так как знаменатель функции f x обращается в ноль при x 1, то прямая x 1 — вертикальная асимптота.

x . При x график функции лежит выше асимптоты, а при x — ниже.

Построение эскиза. Изображаем асимптоты. При x график функции стремится к асимптоте y x 2 снизу, так как

21x 11

0. Можно предположить, что график функции при

x 1 2

достаточно больших отрицательных значениях аргумента является выпуклым вверх.

При стремлении к асимптоте x 1 слева функция стремится к . Можно предположить, что график функции в некоторой левой полуокрестности точки x 1 является выпуклым вверх (к асимптоте).

При стремлении к асимптоте x 1 справа функция стремится к . Можно предположить, что график функции в некоторой правой полуокрестности точки x 1 также является выпуклым вверх (к асимптоте).

При x график функции стремится к асимптоте

21x 11

y x 2 сверху, так как x 1 2 0. Можно предположить, что график функции при достаточно больших значениях аргумента

24

является выпуклым вверх. Так как на промежутке x 1функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 9.1.

Найдем первую и вторую производные функции

Анализ результатов исследования. Заполняя таблицу, учитываем, что в правой и левой окрестностях точки x0 1, поведе-

ние графика функции различно.

25

Построение графика по результатам исследования Замечание. Пункт приведен только для пояснения этапов

анализа результатов исследования и построения графика функции.

На координатной плоскости изображаем вертикальную и наклонные асимптоты.

Так как при x график функции возрастает и имеет выпуклость вверх, то график стремится к наклонной асимптоте снизу. Возрастание продолжается до точки локального максимума

26

D 6; 12,6 . Далее график функции убывает и стремится к вер-

тикальной асимптоте x 1.

Так как график функции является выпуклым вверх, то функция возрастает справа от вертикальной асимптоты x 1до точки максимума C 0;9 , а затем убывает до точки перегиба

tg 243 3,5. На оставшемся промежутке график функции

70

является выпуклым вниз.

а затем функция возрастает, стремясь к асимптоте сверху. График функции изображен на рис. 9.2.

27

28

Функция является нечетной, исследование проводим на по-

асимптотой графика функции при x и при x . Анализ взаимного расположения графика функции и его

асимптот аналогичен примеру 2.

Строим эскиз (рис.10.1). В левой полуплоскости эскиз строим по симметрии для нечетной функции.

Найдем первую и вторую производные

29

Анализ результатов исследования. Результаты исследования объединим в виде таблицы.

Заполняя таблицу, учитываем, что в правой и левой окрест-

ностях точки x0 3, поведение графика функции различно.

Используя свойство нечетности функции, получаем: B 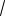6; 46 2,4;9,6 — точка максимума. График функции изображен на рис. 10.2.

30

31

функции неотрицательны, f 6 f 4 0. Асимптоты.

Вертикальных асимптот нет.

Наклонные асимптоты для иррациональной функции находим методом выделения главной части, дополнительный член представления находим для определения взаимного расположения графика и асимптоты.

Так как

x , график лежит ниже асимптоты. Аналогично, из равенства

функции при x , график лежит ниже асимптоты, так как x 0.

32