[Boyd]_cvxslides

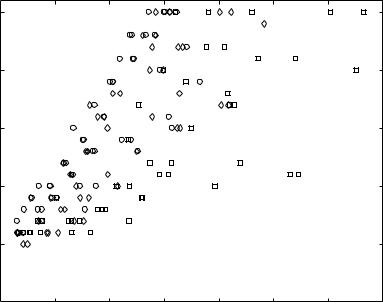
numerical example: 150 randomly generated instances of

minimize f(x) = − Pm log(bi − aT x)

i=1 i

25

•number of iterations much smaller than 375(f(x(0)) − p ) + 6

•bound of the form c(f(x(0)) − p ) + 6 with smaller c (empirically) valid

Implementation

main e ort in each iteration: evaluate derivatives and solve Newton system

H x = g

where H = 2f(x), g = − f(x)

via Cholesky factorization

•cost (1/3)n3 flops for unstructured system

•cost (1/3)n3 if H sparse, banded

example of dense Newton system with structure

Xn

f(x) = ψi(xi) + ψ0(Ax + b), H = D + AT H0A

i=1

•assume A Rp×n, dense, with p n

•D diagonal with diagonal elements ψi′′(xi); H0 = 2ψ0(Ax + b)

method 1: form H, solve via dense Cholesky factorization: (cost (1/3)n3) method 2 (page 9–15): factor H0 = L0LT0 ; write Newton system as

D x + AT L0w = −g, LT0 A x − w = 0 eliminate x from first equation; compute w and x from

(I + LT0 AD−1AT L0)w = −LT0 AD−1g, D x = −g − AT L0w cost: 2p2n (dominated by computation of LT0 AD−1AT L0)

Convex Optimization — Boyd & Vandenberghe

11.Equality constrained minimization

•equality constrained minimization

•eliminating equality constraints

•Newton’s method with equality constraints

•infeasible start Newton method

•implementation

11–1

Equality constrained minimization

•f convex, twice continuously di erentiable

•A Rp×n with rank A = p

•we assume p is finite and attained

optimality conditions: x is optimal i there exists a ν such that

f(x ) + AT ν = 0, Ax = b

equality constrained quadratic minimization (with P Sn+)

optimality condition:

•coe cient matrix is called KKT matrix

•KKT matrix is nonsingular if and only if

Ax = 0, x 6= 0 = xT P x > 0

• equivalent condition for nonsingularity: P + AT A 0

Eliminating equality constraints

represent solution of {x | Ax = b} as

{x | Ax = b} = {F z + xˆ | z Rn−p}

•xˆ is (any) particular solution

•range of F Rn×(n−p) is nullspace of A (rank F = n − p and AF = 0)

reduced or eliminated problem

minimize f(F z + xˆ)

•an unconstrained problem with variable z Rn−p

•from solution z , obtain x and ν as

example: optimal allocation with resource constraint

minimize f1(x1) + f2(x2) + · · · + fn(xn) subject to x1 + x2 + · · · + xn = b

eliminate xn = b − x1 − · · · − xn−1, I.E., choose

reduced problem:

minimize f1(x1) + · · · + fn−1(xn−1) + fn(b − x1 − · · · − xn−1)

(variables x1, . . . , xn−1)

Newton step

Newton step xnt of f at feasible x is given by solution v of

interpretations

•xnt solves second order approximation (with variable v)

•xnt equations follow from linearizing optimality conditions

f(x + v) + AT w ≈ f(x) + 2f(x)v + AT w = 0, A(x + v) = b

Newton decrement

λ(x) = xTnt 2f(x)Δxnt 1/2 = − f(x)T xnt 1/2

properties

• − b gives an estimate of f(x) p using quadratic approximation f:

• directional derivative in Newton direction:

• in general, λ(x) 6= f(x)T 2f(x)−1 f(x) 1/2