
ТФКП методичка
.pdf
x 8. Š®-ä®à¬-ë¥ ®â®¡à ¦¥-¨ï í«¥¬¥-â à-묨 äã-ªæ¨ï¬¨ |
71 |
||||||||||||||
|
|
|
|
´ |
|
|
|
|
|
|
|
|
|
||
» |
|
|
|
|
D |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
¼i |
|
|
||||||
|
0 |
|
2 |
|
|
|
|
|
|
¼i |
D |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
3 |
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
•¨á. 8.27 |
|
•¨á. 8.28 |
|
|
|||||||||
D1, п¢«пойгобп ¯®«®б®© б а §а¥§®¬, в. ¥. |
; 2¸: |
|
|
||||||||||||
|
|
D1 |
= |
½» : 0 < Re » < 2 |
¾ n ·3 |
|
|
||||||||
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||||
‹¨-¥©- ï äã-ªæ¨ï ´ = f2(») = ¼i(1 ¡ 2») ®â®¡à ¦ ¥â ®¡« áâì D1 - ®¡« áâì
D2 |
= f´ : 0 < Im ´ < ¼g n h0; 3 ii |
|
|
¼ |
|
(à¨á. 8.28). ”ã-ªæ¨ï w = f3(´) = e´ ®â®¡à ¦ ¥â ®¡« áâì D2 -
®¡« áâì (à¨á. 8.25) ¯à¨ ® = |
¼ |
|
|
|
|
|
|
|
|
|
|
|
3 . „ «¥¥ á¬. ¯à¨¬¥à 2. |
|
|
||||||
•à¨¬¥à. |
• ©â¨ |
ª®-ä®à¬-®¥ |
®â®¡à ¦¥-¨¥ ®¡- |
|||||||
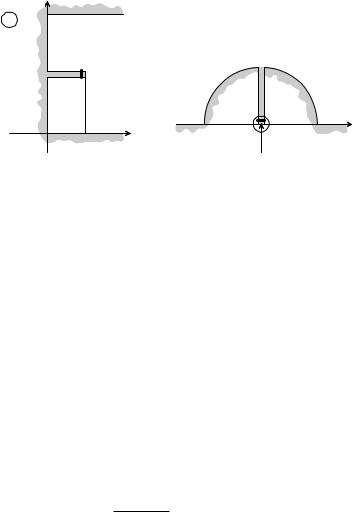
« á⨠D (à¨á. 8.29), ïî饩áï |
¯®«ã¯®«®á®© |
fz : 0 < Im z < |
||||||||
|
£ |
¼i |
¼i |
|
||||||
¯®«ã¯«®áª®áâì. |
|
|
|
2 ; |
2 |
|
¤ |
- |
¢¥àå-îî |
|
< ¼; Re z > 0g á à §à¥§®¬ ¯® ®â१ªã |
|
+ 1 |
||||||||
•¥è¥-¨¥. |
|
|
|
|
|
|
|
|
|
|
”ã-ªæ¨ï » = f1(z) = ez |
®â®¡à ¦ ¥â ®¡« áâì D - |
®¡« áâì |
||||||||
D1 (а¨б. 8.30), п¢«пойгобп ¢¥ае-¥© ¯®«г¯«®бª®бвмо б ¢л¡а®-
è¥--ë¬ ¥¤¨-¨ç-ë¬ ¯®«ãªà㣮¬ ¨ à §à¥§®¬ [i; ei]. ”ã-ªæ¨ï
³ ´
´ = f2 |
(») = 1 |
» + 1 |
®â®¡à ¦ ¥â ®¡« áâì D1 - ¢¥àå-îî ¯®- |
|
2 |
» |
|
«ã¯«®áª®áâì á à §à¥§®¬ [0; i sh 1] ( (à¨á. 8.22) ¯à¨ h = sh 1). „ - «¥¥ ¢®á¯®«ì§®¢ âìáï à¥è¥-¨¥¬ ¯à¨¬¥à 1.
72
y
z¼i
¼i |
D |
|
i |
D1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
»ei |
|
0 |
1 |
x |
0 |
|
|
|
|||
|
•¨á. 8.29 |
|
•¨á. 8.30 |
|
x 9. ‡ ¤ ç¨
‡ ¤ ç¨ á¥¬¥áâ஢®© ª/à ¯® ’”Š• (2001{2002 £.)
1. |
• §«®¦¨âì ¢ àï¤ ‹®à - |
¯® á⥯¥-ï¬ (z ¡ i) äã-ªæ¨î |
||||||||||||||||||||||
|
|
|
f(z) = |
|
|
|
2i + 1 |
|
|
|||||||||||||||
|
|
|
(z ¡ i ¡ 1)(z + i) |
|
|
|
|
|
||||||||||||||||
¢ ª®«ìæ¥, ª®â®à®¬ã ¯à¨- ¤«¥¦¨â â®çª z = |
i |
|
|
|
||||||||||||||||||||
2 . “ª § âì £à -¨æë |
||||||||||||||||||||||||
ª®«ìæ á室¨¬®áâ¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
ˆáá«¥¤®¢ âì ¢á¥ ®á®¡ë¥ â®çª¨ äã-ªæ¨¨ |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
f(z) = |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
¡ |
|
: |
|
|
||||||||||||
|
|
R |
|
|
ez ¡ 1 |
z |
|
|
||||||||||||||||
|
|
|
|
|
|
z |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
|
+1 sin(2 3x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
‚ëç¨á«¨âì ¡1 |
x +4 |
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. |
‚ëç¨á«¨âì |
+i =2 z(cos z ¡1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
jz1 |
+j10 |
|
|
|
|
¡1 |
|
|
dz. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||
5. |
‚ëç¨á«¨âì ¡R2 |
p(x + 2) (1 ¡ x) |
|
|
dx. |
2 |
¡4z) ¢ ¯«®á- |
|||||||||||||||||
6. |
•ãáâì f(z) | ॣã«ïà- ï ¢¥â¢ì äã-ªæ¨¨ Ln(z |
|
||||||||||||||||||||||
ª®á⨠á à §à¥§®¬ ° |
= °1 [ °2, °1 |
= fjz ¡ 2j = 2, Im z 6 0g, |
||||||||||||||||||||||
°2 |
= f¡ Re z = Im z, Im z > 0g, ¯à¨ç¥¬ Im f(¡5) = 0. ‚ëç¨á- |
|||||||||||||||||||||||

x 9. ‡ ¤ ç¨ |
73 |
«¨âì |
|
|
dz |
|
|
|
|
: |
|
|
|
|
|
|
z |
¡ |
2¡2ij=1 |
f(z) ¡ ln 8 ¡ 3¼i |
|
j |
, |
|
|
‡ ¤ ç¨ á¥¬¥áâ஢®© ª/à ¯® ’”Š• (2001{2002 £.)
1. |
• §«®¦¨âì ¢ àï¤ ‹®à - |
¯® á⥯¥-ï¬ z + 1 äã-ªæ¨î |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
f(z) = |
|
|
|
z + i |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
iz2 ¡ 2z + 8i |
|
|
|
|
|
|
||||||||||||||
¢ ª®«ìæ¥, ª®â®à®¬ã ¯à¨- ¤«¥¦¨â â®çª |
z = 2. “ª § âì £à -¨æë |
||||||||||||||||||||||||
ª®«ìæ á室¨¬®áâ¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
• ©â¨ ®á®¡ë¥ â®çª¨ ®¤-®§- ç-®£® å à ªâ¥à |
äã-ªæ¨¨ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
2z + ¼ |
tg z |
|
|
|
|
|
|
||||||||||
|
|
|
|
f(z) = |
|
|
|
exp µ |
|
¶ |
|
|
|
|
|
|
|||||||||
|
|
|
2z ¡ ¼ |
z2 ¡ ¼2 |
|
|
|
|
|
|
|||||||||||||||
¨ ®¯à¥¤¥«¨âì ¨å ⨯. Žâ¢¥â ®¡®á-®¢ âì. |
|
|
|
|
|
|
|||||||||||||||||||
|
•à¨¬¥-ïï ⥮à¨î ¢ëç¥â®¢, ¢ëç¨á«¨âì ¨-â¥£à «ë 3, 4, |
5: |
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
z(z2+1) |
|
|
|
|
+1 |
(x+3) sin3 x |
|
|
|
7 |
5 |
x 7 |
3 x dx |
||||||||||
3. |
|
|
|
|
|
dz. |
4. |
|
|
|
x2+4x+8 |
|
dx. 5. |
¡3 r³x+3¡ ´ |
|
x+4 . |
|||||||||
|
exp |
2 |
¡2 |
|
¡1 |
|
|
|
|||||||||||||||||
|
jz¡2j=4 |
z2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
•ãáâì+ |
g(z) | |
ॣã«ïà-R |
|
|
|
R3 |
|
|
||||||||||||||||
6. |
ï ¢¥â¢ì äã-ªæ¨¨ |
|
(z + 1)(i ¡ z)2 |
||||||||||||||||||||||
¢ ¯«®áª®á⨠á à §à¥§®¬ ¯® ®â१ªã [ 1; i] â ª ï,pçâ® g(0) = 1. |
|||||||||||||||||||||||||
‚ëç¨á«¨âì ¨-â¥£à « |
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
¡ |
||||||||||
|
|
|
|
|
|
|
, |
|
|
|
(z) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
g |
dz: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
z ¡ 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
jzj=2
‡ ¤ ç¨ á¥¬¥áâ஢®© ª/à ¯® ’”Š• (2002{2003 £.)
1. • §«®¦¨âì ¢ àï¤ ‹®à - ¯® á⥯¥-ï¬ (z ¡ 1) ¢ ®ªà¥áâ-®á⨠â®çª¨ z0 = ¡1 äã-ªæ¨î
z + 8
f(z) = (z ¡ 1)(z + 2)2
¨ 㪠§ âì ®¡« áâì á室¨¬®áâ¨.
2. • ©â¨ ¢á¥ ®á®¡ë¥ â®çª¨ äã-ªæ¨¨
cos ¼i
2(z¡1)
f(z) = e¼z + e¼ ;
®¯à¥¤¥«¨âì ¨å ⨯. Žâ¢¥â ®¡®á-®¢ âì.

74
•à¨¬¥-ïï ⥮à¨î ¢ëç¥â®¢, ¢ëç¨á«¨âì ¨-â¥£à «ë 3, 4, 5: |
||||||||||||
j |
¡+j |
z |
R |
|
sin(1¡ 2x) |
. 5. |
R |
|
dx |
|||
|
|
. 4. |
1 x |
2 |
|
|||||||
3. |
|
cos 1 |
+ |
|
3 |
p |
|
x p3 |
|
|
||
|
1¡cos z |
dz |
|
|
|
(2x2+1)2 |
dx |
|
|
|
||
z |
¼ =4 |
|
¡1 |
|
|
|
|
|
|
|
||
6.•ãáâì h(z) | ॣã«ïà- ï ¢¥â¢ì ¬-®£®§- ç-®© äã-ªæ¨¨
Ln |
z+1 |
|
|
|
|
|
2+iz ¢ ¯«®áª®á⨠á à §à¥§®¬ ¯® ªà¨¢®© |
¾ |
[ [¡2; ¡1] |
||||
|
||||||
° = |
½z j jzj = 2; ¡¼ 6 arg z 6 2 |
|||||
|
|
|
¼ |
|
|
|
â ª ï, çâ® Im h(1) = ¡¼2 . • ©â¨ h(0) ¨ ¢ëç¨á«¨âì ¨-â¥£à «
J = |
|
h(z) |
dz: |
|
sin3 z |
||
|
|
|
|
= 1 |
|
|
|
jzj, |
2 |
|
|
‡ ¤ ç¨ á¥¬¥áâ஢®© ª/à ¯® ’”Š• (2003{2004 £.)
1. |
• ©â¨ ¢á¥ ®á®¡ë¥ â®çª¨ äã-ªæ¨¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
z2 sin2 z |
¢ |
sin |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f(z) = |
z¡¼=2 |
sin z |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
e z |
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
(cos z ¡ 1)2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
®¯à¥¤¥«¨âì ¨å ⨯. Žâ¢¥â ®¡®á-®¢ âì. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. |
• §«®¦¨âì ¢ àï¤ ‹®à - ¯® á⥯¥-ï¬ (z ¡ 2 ¡ i) äã-ªæ¨î |
|||||||||||||||||||||||||
|
|
|
|
|
|
f(z) = |
z2 ¡ 2iz + 6 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
z2(z + 3i) |
|
|
|
|
|
|
|
|
|
|
|
||||||
¢ ª®«ìæ¥, ª®â®à®¬ã ¯à¨- ¤«¥¦¨â â®çª |
z = 5 + i. “ª § âì £à - |
|||||||||||||||||||||||||
-¨æë ª®«ìæ |
á室¨¬®áâ¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. |
•à¨¬¥-ïï ⥮à¨î ¢ëç¥â®¢, ¢ëç¨á«¨âì ¨-â¥£à «ë 3, 4, 5: |
|||||||||||||||||||||||||
j |
•ãáâì+ j |
g(z) | ॣã«ïà-R ï ¢¥â¢ì ¬-®£®§-R |
ç-®© äã-ªæ¨¨ |
|||||||||||||||||||||||
3. |
|
|
|
z¡1 1 |
|
|
+1 x cos(2 |
¡ |
x) |
|
|
|
|
2 |
|
(2 |
¡ |
x)3 |
1 dx. |
|||||||
|
|
|
dz. 4. |
|
2 |
|
|
dx. 5. |
|
5 |
|
|
3 |
|||||||||||||
|
z+1+i =2 |
(z+1) sin z |
|
¡1 |
|
4x +1 |
|
|
|
|
1 |
q(x¡1) |
|
¢ x |
||||||||||||
fp |
|
g ¢ ¯«®áª®á⨠á à §à¥§®¬ ¯® ªà¨¢®© |
|
|
|
|
|
|
|
|||||||||||||||||
1 + 4z2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
° = ½z j |
|
jzj = 2; |
|
2 6 arg z 6 2¼¾ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
â ª ï, çâ® g(0) = 1. •ãáâì f(z) = |
|
|
z |
|
|
|
res f ¨ ¢ë- |
|||||||||||||||||||
(g(z)+3)2 |
. • ©â¨ |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x 9. ‡ ¤ ç¨ |
75 |
ç¨á«¨âì ¨-â¥£à «
J = |
|
|
|
f(z) dz: |
z = |
1 |
|
||
|
|
|
||
j j |
,p2 |
|||
‡ ¤ ç¨ á¥¬¥áâ஢®© ª/à ¯® ’”Š• (2005{2006 £.)
1. |
• §«®¦¨âì ¢ àï¤ ‹®à - |
|
|
¯® á⥯¥-ï¬ (z ¡ 3) äã-ªæ¨î |
|
|||||||||||||||||||
|
|
|
f(z) = |
2z + i |
|
|
+ |
|
|
|
z + 8 + 6i |
|
|
|
|
|
|
|
||||||
|
|
|
(z + 2i)2 |
z2 + 2z(i ¡ 2) ¡ 8i |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
¢ ª®«ìæ¥, ª®â®à®¬ã ¯à¨- ¤«¥¦¨â â®çª |
z = 0. • ©â¨ à ¤¨ãáë |
|||||||||||||||||||||||
ª®«ìæ á室¨¬®áâ¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
• ©â¨ ¢á¥ ®á®¡ë¥ â®çª¨ äã-ªæ¨¨ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cos ³ |
|
´ |
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
f(z) = |
iz¡z2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2¼ |
3 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
³e z ¡ 1´ |
|
|
|
|
|
|
|
|
|
||||||
®¯à¥¤¥«¨âì ¨å ⨯. Žâ¢¥â ®¡®á-®¢ âì. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
•à¨¬¥-ïï ⥮à¨î ¢ëç¥â®¢, ¢ëç¨á«¨âì ¨-â¥£à «ë 3, 4, 5: |
|||||||||||||||||||||||
|
j |
¡+j |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
R |
1) p |
|
|
|
|
|
|
|
|
iz |
|
|
+1 (6x |
|
1) Sin(1 |
|
|
2x) |
|
|
+1 ln(x |
x |
|
1 |
|
|||||||
3. |
|
e |
|
dz. 4. |
|
¡ |
|
|
2 |
|
|
¡ |
|
dx. 5. |
¡ 2¢ |
|
¡ |
|
|
dx. |
||||
|
2 |
z |
|
|
|
|
|
|
|
|
||||||||||||||
|
ch |
|
¡1 |
4x |
+4x+5 |
|
|
1 |
|
x |
|
|
|
|
||||||||||
|
z |
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.•ãáâì f(z) | ॣã«ïà- ï ¢¥â¢ì ¬-®£®§- ç-®© äã-ªæ¨¨
³´
Ln |
z¡1 |
¢ ®¡« á⨠G = |
z |
z |
> 1 |
g |
â ª ï, çâ® f( ) = 0. |
||
|
z+1 |
|
f |
j j j |
|
|
1 |
||
„®ª § âì, çâ® ¬-®£®§- ç- ï äã-ªæ¨ï |
p |
f(z) + 4i |
à ᯠ¤ ¥âáï ¢ |
||||||
G - |
ॣã«ïà-ë¥ ¢¥â¢¨. |
|
|
|
|
|
|||
ª ï, çâ® g(1) = ¡p2(i + 1). ‚ëç¨á«¨âì ¨-â¥p |
|
|
|||||
•ãáâì g(z) | ॣã«ïà- ï ¢¥â¢ì äã-ªæ¨¨ f(z) + 4i ¢ G â - |
|||||||
|
|
|
£à « |
|
|||
|
|
J = |
, |
dz |
|||
|
|
|
: |
||||
|
|
g(z) |
|||||
jzj=2
76
x 10. Žâ¢¥âë
Žâ¢¥âë ª ᥬ¥áâ஢®© ª/à ¯® ’”Š• (2001{2002 £.)
8 z : jz ¡ ij < 1. |
|
|
|
P |
|
nP |
|
|||||
1. |
1 |
1 |
|
+1 |
n |
+1 (¡1)n |
n, |
|||||
|
f(z) = |
z¡i¡1 |
¡ |
z+i |
|
= ¡ n=0(z ¡ i) ¡ =0 |
(2i)n+1 |
(z ¡ i) |
||||
2. |
zk = 2¼ki, k 2 Z, k 6= 0 | ¯®«îá |
1-£® ¯®à浪 ; z = 0 | |
||||||||||
ãáâà. ®. â.; z = 1 | -¥¨§®«. ®. â. |
|
|
|
|
||||||||
3. |
I = ¼2 e¡6 ¢ sin 2. |
|
|
|
|
|
||||||
4. |
I = ¼i3 . |
|
|
|
|
|
|
|
|
|||
5. |
I = |
9¼ |
. |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
||||
6. |
I = ¡4¼. |
|
|
|
|
|
|
|
|
|||
Žâ¢¥âë ª ᥬ¥áâ஢®© ª/à ¯® ’”Š• (2001{2002 £.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||||
1. |
|
f(z) = ¡ |
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
; |
|
t |
|
= z + 1 |
|
f(t) = ¡ |
|
|
|
¡ |
||||||||||||||||||||||||||||||||||||||||||||
2(z+4i) |
|
|
2(z¡2i) |
|
|
2(t¡1+4i) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
i=2 |
|
|
|
|
|
|
+ |
|
|
|
|
|
i=2 |
|
|
|
= |
|
+1 |
|
|
i=2 |
|
tn |
|
|
||||||||||||||||||||
¡ |
2(t |
|
1 |
|
|
2i) |
|
|
|
(1 |
|
|
|
4i)(1 |
|
|
t |
) |
|
|
|
|
|
|
t(1 |
|
1+2t i ) |
|
|
e |
|
|
|
|
(1 |
|
4i)n+1 |
|
|
|
|
¡ |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 4i |
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
¡ ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
¡ |
|
+1 i(1+2i)n¡1 |
|
|
|
¡ |
|
|
|
|
|
|
¡ ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
P |
¡ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
=1 |
|
|
|
2tn |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
nP |
|
+1 |
|
|
|
i=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡1 |
|
|
|
|
|
i(z+1)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p5 < jz + 1j < p17. |
||||||||||||||||||||||||||||||||||
f(z) = n=0 |
|
|
|
(z + 1)n ¡n= |
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(1¡4i)n+1 |
¡1 |
2(1+2i)n+1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
P2z+¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg z |
|
. |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2. f(z) = 2z¡¼ exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
z2¡¼2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ¯à¥¤.á.®.â. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
z = |
|
|
¼ |
| ã.®.â.; |
|
z |
|
= ¼=2 + ¼k | á.®.â; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
§ |
|
|
|
|
|
|
|
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
´ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. ¡16¼i.+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. I = 43 |
|
|
|
(x + 3) sin x |
|
|
|
|
|
|
|
|
|
|
(x + 3) sin 3x |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx ¡41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 + 4x + 8 |
|
|
|
|
|
x2 + 4x + 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
¡1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 2i | ¯®«îá 1 ¯®à浪 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
¡ ¡ |
|
|
|
| |
|
|
|
|
|
|
iz |
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
| |
|
|
|
|
|
|
|
|
{z |
|
|
|
|
i( 2+2i) |
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
{z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
f |
|
(z) = |
|
|
|
|
|
|
(z+3)e |
|
|
|
|
|
|
|
|
|
|
|
|
a = res |
¡2+2i |
f |
1 |
= (1+2i)e ¡ |
|
|
|
= e¡ |
|
|
(1 + |
||||||||||||||||||||||||||||||||||||||
|
|
(z+2+2i)(z+2 |
|
2i) ; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4i |
|
|
|
|
4i |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ 2i)(cos 2 ¡ i sin 2), |
³ |
¼e¡2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¼e¡2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
I |
|
|
= Im(2¼ia) = Im |
(1 + 2i)(cos 2 i sin 2) |
|
= |
(2 cos 2 |
¡ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 sin 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
´ |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 10. |
|
Žâ¢¥âë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
||||||||||||||
f2 = |
|
|
|
|
(z+3)e3iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(z+2+2i)(z+2¡2i) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b = res¡2+2i f2 = |
(1+2i)e3i(¡2+2i) |
|
|
|
|
|
|
|
6 |
(1 + 2i)(cos 6 ¡ i sin 6), |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4i |
|
|
|
|
|
|
|
= e4¡i |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
I2 |
¼e¡6= |
|
|
|
Im(2¼ib) . |
= |
|
|
|
|
Im |
³ |
¼e¡6 |
(1+2i)(cos 6¡i sin 6)´ |
|
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
(2 cos 6 |
¡ |
sin 6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
I = |
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8 |
|
3e¡2(2 cos 2 ¡ sin 2) ¡ e¡6(2 cos 6 ¡ sin 6) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
5. |
|
|
|
|
|
¼¡ |
|
(10 |
¡ |
4 |
¢ |
113=5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
sin 35¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
i |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
43 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
g(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6. J |
|
= ¡2¼i(¡C¡1) = 2¼ie |
4¼i |
|
1 + 31 ¡ 23i |
|
= |
34¼(1 + |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ 2i)e |
¼i |
|
J = ¡2¼i |
res1 f |
|
f = z¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 ;i |
|
(0+2 arctg x), |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x > 2: g(x) = (¡1) 3 (x + 1)(x2 + 1)e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
+ |
1 |
|
|
i¼+ |
2i |
|
arctg x |
|
|
¡ |
|
|
4¼i |
|
g(z) e |
4¼i |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
e |
3 |
|
|
|
|
e |
3 , â.¥. |
3 |
z |
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
= |
|
|
|
|
1 + x |
|
|
1p x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!!1 |
|
|
|
|
|
. |
|
» |
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
z |
|
4¼i |
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
9 g1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
¢1 |
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(z) |
|
|
(z¡) 2 1¢ |
¡ z¡ |
|
i |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
‘ ¤àã£q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1=3 |
|
|
2=3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
®© áâ®à®-ë, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
¢¡ |
|
|
|
|
z ¢ |
|
2 p1 1 + z |
|
1 ¡ |
|
|
|
|
|
9 g0(z) 2 |
|||||||||||||||||||||||||||||
p1¡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
= e¢ |
3 |
|
. g0(z) = 1 + |
31z |
|
|
|
|
|
9z2 +¡: : : ; g¢1(z) = 1 |
|
3z + : : : ; |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 + |
1 |
|
|
1=3, |
|
g ( ) = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
2=3, |
|
g ( ) = 1, â.¥. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3 |
|
|
|
j |
|
|
|
|
|
|
|
4¼i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
2i |
|
|
|
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 1=z = e 3¡ |
|
|
|
¢¡z + o(z ) 1 +¢z + : : : , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
g(z) |
|
|
= e |
3 4¼i1 + |
1 |
|
+ o(z1 ) 1 ¡ |
2i |
+ o(z1 ) , jzj > 1. |
|
f(z) = |
||||||||||||||||||||||||||||||||||||||||||||||||||
z |
|
|
|
¡ |
3z |
|
3z |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
¡ |
|
¡ |
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
¢¡ |
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
g(z)=z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2i |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Žâ¢¥âë ª ᥬ¥áâ஢®© ª/à ¯® ’”Š• (2002{2003 £.)
1. |
|
|
|
|
|
1 |
|
|
|
1 (¡1)n+1 |
|
|
|
|
|
|
|
n, |
|
|
|
. |
|||||
|
f(z) = |
z¡1 |
+ |
|
=1 |
|
|
3n+2 |
(2n + 5)(z ¡ 1) |
|
0 < jz ¡ 1j < 3 |
|
|||||||||||||||
2. |
|
|
|
|
|
|
|
|
|
nP |
|
|
| ¯®«îá 1-£® ¯®à., |
k 6= 0; ¡1 |
; |
|
|||||||||||
|
zk = 1 + (1 + 2k)i |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
z = 1 § i | ã.®.â., |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z = 1 | á.®.â.; z = 1 | ¯à¥¤. â. ¯®«îᮢ . |
|
|
|
|
|||||||||||||||||||||||
3. |
res f = 0, |
res f = |
|
|
1 |
sin |
|
1 |
|
I = |
i |
sin |
1 |
|
|
|
|||||||||||
|
|
2 |
2¼ ; |
|
2¼ . |
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
2¼ |
|
|
2¼ |
|
¼ |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
¡¼ cos8e |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
2¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p4¢p3 . |
|
|
¡ |
45 + ln 2¢, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6. |
J = 2¼2 ¡ ¼i |
h(0) = ¡ ln 2 ¡ 2¼i. |
|
|
|||||||||||||||||||||||

78
Žâ¢¥âë ª ᥬ¥áâ஢®© ª/à ¯® ’”Š• (2003{2004 £.)
1. |
z = ¡¼2 , zk = ¼4 + ¼k2 |
|
| ¯®«îáë 1-£® ¯®à浪 , |
|
|
|
|||||||||||||||||||||||||
zl |
= ¼l | ‘.Ž.’., 1 | -¥¨§®«. Ž.’. |
P |
¡ |
|
|
|
|
|
|
|
|||||||||||||||||||||
3. |
I = 4¼(e ¡ z). p |
|
|
nP |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
+1 (z i)n |
|
+1 |
i |
n |
|
|
|
|||||||||||
2. |
f(z) = |
z¡4i |
+ |
z¡2i |
= |
=0 3 |
n¡n+1 |
+ |
|
|
|
|
n+1 |
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
n=0 |
(z i) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
I = 2¼ sin 12 |
e¡ 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
p |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
I = |
4p |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)n, R = p |
|
|
|||||||
6. |
|
(z) = 2¼i+ln z+ 1 |
(¡1)n¡1 |
|
|
1 |
|
|
1 |
|
|
|
(z |
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
S ¡¡ |
5 ¢ = 2¼i + ln |
25 .P |
|
n |
|
³ |
(1+i)n + (1¡i)n ´ |
¡ |
|
|
|||||||||||||||||||||
|
f |
1 |
|
|
|
|
|
|
|
26 |
|
|
1 |
|
|
|
|
||||||||||||||
Žâ¢¥âë ª ᥬ¥áâ஢®© ª/à ¯® ’”Š• (2005{2006 £.)
|
k |
2 |
|
|
|
, |
|
|
|
|
P |
|
|
|
|
|
|
p |
P . |
|
|
||||
|
|
|
|
|
|
3 |
|
3i |
|
|
|
¡1 |
|
|
|
|
|
|
k |
|
|
+1 |
k+1 |
|
|
1. |
f(z) = |
z¡4 |
¡ |
(z+2i)2 |
|
= |
|
|
3(z¡3) |
|
+ |
|
3i(k+1)(¡1) |
(3+ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k=¡1 |
|
|
|
|
|
|
|
k=0 |
|
|
|||
+ 2i)¡ ¡ (z |
¡ |
3 K = |
f |
z |
j |
1 < |
j |
z |
¡ |
3 |
< |
13 |
) |
|
|
||||||||||
2. |
, |
|
i |
|
|
|
|
|
|
|
j i |
|
|
|
g |
|
|
||||||||
¡i |
|
|
|
| ¯®«îá 1-£® ¯®à浪 ; |
|
|
| ¯®«îá |
3-£® ¯®à浪 , |
|||||||||||||||||
3 |
k |
|
|||||||||||||||||||||||
K 2 Zn f¡1, 0, 1, 3g, i | ‘Ž’; 0 | â®çª |
- ª®¯«¥-¨ï ¯®«îᮢ; |
||||||||||||||||||||||||
1 | ¯®«îá 3-£® ¯®à浪 .
3. 2¼e¡¼2 .
4. ¡¼e2¡2 (3 cos 2 + 2 sin 2).
5. ¼.
6. ¼(i¡1)
4p2 .
