
ТФКП методичка
.pdf
x 7. ‚ëç¨á«¥-¨¥ -¥á®¡á⢥--ëå ¨-â¥£à «®¢ |
51 |
•â®â ¨-â¥£à « à ¢¥- -ã«î, â ª ª ª äã-ªæ¨ï eiz=z ॣã«ïà-
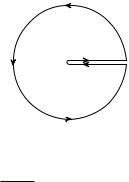
¢-ãâਠª®-âãà ¡½;R. ‘ ¤à㣮© áâ®à®-ë, ®- à ¢¥- á㬬¥ ¨-⥣- à «®¢, ¢§ïâëå ¯® ¯®«ã®ªàã¦-®áâï¬ ¡½, ¡R ¨ ®â१ª ¬ [¡R; ¡½], [½; R]. ˆ¬¥¥¬
eiz = 1 + h(z); z z
£¤¥ h(z) | äã-ªæ¨ï, ॣã«ïà- ï ¢ â®çª¥ z = 0. …᫨ z 2 ¡½, â®
z = ½ei'; 0 6 ' 6 ¼; dz = i½ei' d'
¨
|
0 |
|
|
Z |
1 |
dz = i Z¼ |
d' = ¡i¼: |
|
|||
z |
|||
¡½ |
|
|
|
”ã-ªæ¨ï h(z) ®£àR -¨ç¥- ¢ ®ªà¥áâ-®á⨠â®çª¨ z = 0 ¨, á«¥- ¤®¢ ⥫ì-®, "1(½) = h(z) dz ! 0, ¯à¨ ½ ! +0. Žâáî¤ ¯®«ã-
ç ¥¬
¡½
Z eiz
z dz = ¡i¼ + "1(½):
¡½
•® «¥¬¬¥ †®à¤ - "2(R) = R eziz dz áâ६¨âáï ª -ã«î ¯à¨
¡R
R ! +1. „ «¥¥, á㬬 ¨-â¥£à «®¢ ¯® ®â१ª ¬ [¡R; ¡½], [½; R] à ¢-
Z x |
Z½ x |
Z½ |
|
x |
Z½ |
x |
|
||||||
¡½ |
eix |
dx + |
R |
eix |
dx = |
R |
eix ¡ e¡ix |
dx = 2i |
R |
sin x |
dx: |
|
|
|
|
|
|
|
|||||||||
¡R |
|
|
|
|
|
|
|
|
|
|
|
||
‘«¥¤®¢ ⥫ì-®, |
|
|
|
x |
dx ¡ i¼ + "1(½) + "2(R); |
(5) |
|||||||
|
0 = I½;R = 2i Z½ |
||||||||||||
R
sin x
£¤¥ "1(½) ! 0 (½ ! +0), "2(R) ! 0 (R ! +1). ’ ª ª ª ¨-⥣-
52
à « I á室¨âáï, â® áãé¥áâ¢ã¥â
|
|
R |
|
|
|
lim |
Z |
sin x |
dx = I: |
R |
|
|||
!+ |
x |
|||
½ |
+0 |
|
|
|
! 1 ½
•¥à¥å®¤ï ¢ á®®â-®è¥-¨¨ (5) ª ¯à¥¤¥«ã ¯à¨ ½ ! +0, R ! +1,
¯®«ãç ¥¬ 2iI ¡ i¼ = 0, ®âªã¤ |
I = ¼=2. |
|
|
|
|
|
|
||||||||
•à¨¬¥à. ‚ëç¨á«¨âì ¨-â¥£à « |
|
|
|
|
|
|
|
|
|
||||||
|
|
+1 |
px |
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
I = Z0 |
|
dx: |
|
|
|
(6) |
|||||||||
(x + 8)2 |
|
|
|
||||||||||||
•¥è¥-¨¥. ‚ ª®¬¯«¥ªá- |
®© ¯«®áª®á⨠á à §à¥§®¬ ¯® «ãçã |
||||||||||||||
«ïà-®© ¢¥â¢ìî ¬-®£®§- çp |
|
|
|
|
|
|
|
|
|
x |
|
||||
[0; +1) äã-ªæ¨ï f(z) = |
3 jzjei'=3, 0 < ' < 2¼, ï¥âáï ॣã- |
||||||||||||||
D |
|
|
|
|
|
|
|
|
z© < |
ª |
|
|
|
||
• áᬮâਬ ®¡« áâì |
-®© äã-ªæ¨¨ |
|
p3 z |
( |
|
, |
18{19). |
||||||||
|
| ªà㣠|
f |
z : |
j |
j |
R |
|
R > 8, á à §à¥- |
|||||||
|
|
|
|
|
|
|
g |
|
|
||||||
§®¬ ¯® à ¤¨ãáã [0; R]. ƒà -¨æ |
í⮩ ®¡« á⨠¡ = °+ [ CR [ °¡, |
||||||||||||||
£¤¥ °+ | ¢¥àå-¨© ¡¥à¥£ à §à¥§ , CR | ®ªàã¦-®áâì fz : jzj =
= Rg, °¡ | -¨¦-¨© ¡¥à¥£ à §à¥§ , ®à¨¥-â æ¨ï ªà¨¢®© ¡ ¯®ª - § - - (à¨á. 7.3).
CR
D
°+
¡8 0 °¡ R
•¨á. 7.3
”ã-ªæ¨ï g(z) = f(z)2 ॣã«ïà- ¢ ®¡« á⨠D, § ¨áª«îç¥-
(z+8)
-¨¥¬ â®çª¨ z = ¡8 | ¯®«îá ¢â®à®£® ¯®à浪 , ¨ -¥¯à¥àë¢-
x 7. ‚ëç¨á«¥-¨¥ -¥á®¡á⢥--ëå ¨-â¥£à «®¢ |
53 |
®ª®«® ¡ ¢¯«®âì ¤® ¡. •® ⥮६¥ ® ¢ëç¥â å ¯®«ãç ¥¬
|
|
|
|
|
|
Z |
|
g(z) dz = 2¼i res g(z); |
â. ¥. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=¡8 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f(z) |
|
|
|
|
|
|
f(z) |
|
|
|
|
(z) |
|
|
|
|
|
|||||||||||||
Z |
|
|
dz + Z |
|
|
|
|
|
|
|
dz + Z |
f |
dz = |
|
|
|
|||||||||||||||
(z + 8)2 |
(z + 8)2 |
(z + 8)2 |
|
|
|
||||||||||||||||||||||||||
CR |
|
|
|
°+ |
|
|
|
|
|
|
|
|
|
°¡ |
|
|
|
|
|
|
|
|
|
|
f(z) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2¼i res |
|
: (7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z + 8)2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=¡8 |
|
|||
•®ª ¦¥¬, ª ª á ¯®¬®éìî í⮣® à ¢¥-á⢠|
¬®¦-® ¢ëç¨á«¨âì |
||||||||||||||||||||||||||||||
¨-â¥£à « (6). • áᬮâਬ ¯®®ç¥à¥¤-® ç«¥-ë à ¢¥-á⢠|
(7). |
||||||||||||||||||||||||||||||
|
1. Žæ¥-¨¬ ¨-â¥£à « |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
IR = Z |
|
(z) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
dz: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z + 8)2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•à¨ jzj = R ¯®«ãç ¥¬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
jf(z)j = p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
R; jz + 8j > jjzj ¡ 8j = R ¡ 8 > 0; |
|
|
|||||||||||||||||||||||||||
®âªã¤ |
1 |
|
6 |
|
1 |
. •®í⮬ã |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
jz+8j |
R¡8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
jIRj 6 |
|
|
R |
¢ 2¼R ! 0 |
¯à¨ |
|
|
R ! +1: |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
(R ¡ 8)2 |
|
|
|
||||||||||||||||||||||||||
2. |
…᫨ z 2 °+, â® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
f(z) = f(x + i0) = p3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x; x > 0: |
|
|
|
||||||||||||||||||||||
•®í⮬ã |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z) |
|
|
R |
|
|
|
p3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||
|
|
|
|
|
I1 = |
°Z+ |
f |
dz = Z0 |
|
|
|
dx: |
|
|
|
||||||||||||||||
|
|
|
|
|
(z + 8)2 |
|
(x + 8)2 |
|
|
|
|||||||||||||||||||||
Žâ¬¥â¨¬, çâ® ¯à¨ R ! +1 íâ®â ¨-â¥£à « áâ६¨âáï ª ¨áª®- ¬®¬ã ¨-â¥£à «ã (6).
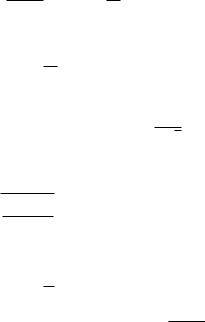
54
3. |
…᫨ z 2 °¡, â® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f(z) = f(x ¡ i0) = p3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
xe2¼i=3; x > 0: |
|
|
|
|||||||||||||||
•®í⮬㠨-â¥£à « |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f(z) |
|
|
R |
|
|
p3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||
I2 =°Z |
|
dz = ¡e2¼i=3 |
Z0 |
|
dx = ¡e2¼i=3 ¢ I1: |
||||||||||||||||
(z + 8)2 |
(z + 8)2 |
||||||||||||||||||||
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
•à ¢ ï ç áâì à ¢¥-á⢠|
|
(7) -¥ § ¢¨á¨â ®â R ¯à¨ R > 8 |
||||||||||||||||||
¨ à ¢- |
¢ z=¡8 (z + 8)2 |
|
0(z)¯z= |
|
8= 2¼i 3z |
¯z= |
|
8 = |
|||||||||||||
|
|
|
¡ |
¡ |
|||||||||||||||||
|
|
|
|
f(z) |
|
|
¯ |
|
|
|
|
|
|
f(z) |
¯ |
|
|||||
|
2¼i |
|
res |
|
|
= 2¼if |
|
¯ |
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
=2¼i ¢ 3(¡2 8)e¼i=3 = ¡¼i6 e¼i=3:
‚१ã«ìâ ⥠¨§ à ¢¥-á⢠(7) ¯à¨ R ! +1 ¯®«ãç ¥¬
³1 ¡ e2¼i=3´I = ¡¼i6 e¼i=3;
®âªã¤
I = |
|
¼ie¼i=3 |
|
= ¼ |
|
|
|
1 |
|
= |
¼ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
6 ¡1 ¡ e |
2¼i=3 |
¢ 12 e |
¼i=3 |
e ¼i=3 |
|
12 sin |
¼ |
|||||
|
|
|
¡2i |
¡ |
|
3 |
||||||||
¼
= 6p3: N
•à¨¬¥à. ‚ëç¨á«¨âì ¨-â¥£à «
I = Z2 s5 (2 ¡ x)3 dx:
(x ¡ 1)3
1
•¥è¥-¨¥. „«ï ¢ëç¨á«¥-¨ï í⮣® ¨-â¥£à « á ¯®¬®éìî ¢ë- ç¥â®¢ ॣã«ïà-® ¯à®¤®«¦¨¬ ¯®¤ë-â¥£à «ì-ãî äã-ªæ¨î á ¨-- â¥à¢ « (1; 2] ¢ -¥ª®â®àãî ®¡« áâì ¢ C, £à -¨æ ª®â®à®© ᮤ¥à-
¦¨â ®â१®ª [1; 2]. ’ ª ª ª ¯®¤ë-â¥£à «ì- ï äã-ªæ¨ï ¯à¨ ¯à®- |
|||||||
â® -¥®¡å®¤¨¬® ¯®§ ¡®â¨âìáï ® ¢®§¬®¦-®á⨠¢ë¤¥«¥-¨ïn |
ॣã«ïào- |
||||||
¤®«¦¥-¨¨ ¢ |
|
|
áâ -®¢¨âáï ¬-®£®§- ç-®© äã-ªæ¨¥© |
|
(2¡z)3 |
||
C |
5 |
||||||
|
|
|
|
q(z¡1)3 , |
|||
-ëå ¢¥â¢¥© í⮩ äã-ªæ¨¨ ¢ ¯®«ãç¥--®© ®¡« |
áâ¨. |
‘«¥¤ãï à¥- |
|||||
|
|
|
|
||||
§ã«ìâ â ¬ x 18{19, ¯®«ãç ¥¬, çâ® ¢ ®¡« á⨠C n [1; 2] |
ã äã-ªæ¨¨ |
||||||
x 7. ‚ëç¨á«¥-¨¥ -¥á®¡á⢥--ëå ¨-â¥£à «®¢ |
55 |
||
y |
|
|
|
|
Cr |
° |
|
|
°r+ |
|
|
|
|
|
|
0 |
1 |
°r¡ 2 |
x |
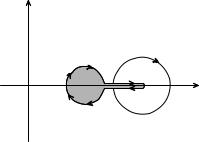
•¨á. 7.4
nq |
|
o |
f(z) |
|
f(x + i0) > 0 |
|
x 2 (1; 2) |
|
|
3 |
|
|
|
|
|
|
|
5 (2¡z)3 |
áãé¥áâ¢ãîâ ॣã«ïà-ë¥ ¢¥â¢¨. ‚롥६ â ªãî ¥¥ |
|||||||
|
(z¡1) |
|||||||
ॣã«ïà-ãî ¢¥â¢ì |
|
, ã ª®â®à®© |
|
¯à¨ |
|
. |
||
…᫨ ¤«ï à §à¥§ |
[1; 2] ¢¢¥áâ¨, ª ª ¨ ¢ ¯à¥¤ë¤ã饩 § ¤ ç¥, ¤¢ |
|
||||||
¡¥à¥£ : ¢¥àå-¨© °+ ¨ -¨¦-¨© °¡, â® íâ ¢¥â¢ì f(z) -¥¯à¥àë¢-® ¯à®¤®«¦¨¬ - £à -¨æã °+ [ °¡ ¢áî¤ã, ªà®¬¥ â®çª¨ 1. —⮡ë
¢ë¯®«-﫨áì ãá«®¢¨ï â¥®à¥¬ë Š®è¨ ® ¢ëç¥â å, -ã¦-® ¨áª«î- ç¨âì â®çªã 1 ¨§ £à -¨æë ¨ à áᬮâà¥âì ®¡« áâì
D(r) = |
C |
n ([1; 2] [ fz : jz ¡ 1j 6 rg) ; £¤¥ |
r 2 (0; 1): |
‚ í⮩ ®¡« á⨠äã-ªæ¨ï f(z) ¢áî¤ã ॣã«ïà- |
(ªà®¬¥ 1) ¨ |
||
-¥¯à¥àë¢-® ¯à®¤®«¦¨¬ ¢¯«®âì ¤® ¥¥ £à -¨æë ¡r = Cr[°r+[°r¡,
£¤¥ ®ªàã¦-®áâì Cr = fz : jz ¡ 1j = rg ®à¨¥-â¨à®¢ - |
¯® 室ã |
ç ᮢ®© áâ५ª¨, °r+ | ¢¥àå-¨© ¡¥à¥£ à §à¥§ ®â१ª |
[1 + r; 2] |
á ®à¨¥-â 樥© ®â â®çª¨ 1 + r ¤® â®çª¨ 2, °r¡ | -¨¦-¨© ¡¥à¥£ à §à¥§ ®â१ª [1 + r; 2] á ®à¨¥-â 樥© ®â â®çª¨ 2 ¤® â®çª¨ 1 +
+r. ’ ª¨¬ ®¡à §®¬ ¢ë¡à -- ï ®à¨¥-â æ¨ï £à -¨æë ¡r ï¥âáï ¯®«®¦¨â¥«ì-®© ¤«ï ®¡« á⨠D(r).
’ ª ª ª ¢ ®¡« á⨠D(r) äã-ªæ¨ï f(z) ¨¬¥¥â ¥¤¨-á⢥--ãî ®á®¡ãî â®çªã z = 1, â® ¯® ⥮६¥ Š®è¨ ® ¢ëç¥â å ¯®«ãç ¥¬
Z+ |
+ Z |
dz + Z |
= 2¼i z=1 |
|
f(z) dz |
f(z) |
f(z) dz |
res f(z): |
(8) |
°r |
Cr |
°r¡ |
|
|
•®ª ¦¥¬, çâ® ¢â®à®¥ á« £ ¥¬®¥ «¥¢®© ç á⨠(8) áâ६¨âáï ª

56
-ã«î ¯à¨ r ! +0. ˆ¬¥¥¬ |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
¯ |
f(z) dz¯ 6 |
f(z) dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
¯Z |
¯ |
|
Z j |
|
|
jj |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯Cr |
¯ |
Cr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
¯ |
1 + r |
|
3=5 |
|
|
|
|
|
|
1 + r |
|
|
3=5 |
|
|
|
¯à¨ |
|
|||||||||
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
6 Z µ |
|
|
|
¶ |
|
jdzj = µ |
|
|
|
|
|
|
|
¶ |
|
2¼r ! 0 |
|
r ! +0: |
|||||||||
|
|
r |
|
|
|
r |
|
|
|
|
|
|
||||||||||||||||
|
Cr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
5 |
|
|
2 |
x |
|
3 |
, |
|
|
|
|
|
|
|
|
|||||
|
…᫨ x 2 °r , â® f(x) = r³x¡¡1 |
´ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Z |
|
|
|
|
|
Z2 |
f(x) dx ! I |
|
|
|
|
|
r ! +0: |
|
|||||||||||||
|
f(z) dz = |
|
|
|
|
¯à¨ |
(9) |
|||||||||||||||||||||
|
+ |
|
|
|
|
1+r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
°r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…᫨ x 2 °r¡, â® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
f(x) = s5 |
µ |
2 |
¡ |
x |
¶ |
3 |
|
6¼ |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
e¡i |
|
; |
|
|
|||||||||||||||
|
|
|
|
|
x |
1 |
|
|
5 |
|
|
|||||||||||||||||
â ª ª ª |
|
|
|
¡ |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
¢° arg |
2 ¡ z |
|
|
3 |
|
= |
|
6¼; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
µz ¡ 1¶ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
£¤¥ ° = fz : jz ¡ 2j = "; 0 < " < 1g | ®ªàã¦-®áâì, ®à¨¥-â¨à®-
ᮢ®© áâ५ª¨. •®í⮬ã |
|
|
|||
¢ -- ï ¯® 室ãZ fç(z) dz ! ¡e¡6¼i=5I |
¯à¨ r ! +0: |
|
(10) |
||
°r¡ |
|
|
|
|
|
• ©¤¥¬ res f(z) = |
c |
, £¤¥ c |
| ª®íää¨æ¨¥-⠯ਠ|
1 |
àï¤ |
z=1 |
¡ ¡1 |
¡1 |
|
z |
|
‹®à - äã-ªæ¨¨ f(z) ¢ ®ªà¥áâ-®á⨠â®çª¨ z = 1. …᫨ x 2 R ¨ x > 2, â®
f(x) = s5 |
¯ |
(2 x)3 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3=5 |
1 ¡3=5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
µ1 ¡ x¶ |
|
|||||||||
¯3¼i |
¡ |
1)3 |
¯6 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||
¯ |
(x |
|
¯e¡i3¼=5 |
= e¡3¼i=5 µ1 ¡ x¶ |
|||||||||||||||||||||||||
¯ |
|
µ |
|
¡ |
5x |
|
|
|
¶µ |
|
5x |
¶ |
|
|
|
|
|||||||||||||
|
|
1 |
|
|
¯ |
|
|
+ : : : |
1 + |
|
|
|
+ : : : = |
|
|
|
|
||||||||||||
= e¡ |
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
= e¡3¼i=5 |
µ1 + µ |
|
|
¡ |
|
¶ |
|
+ : : :¶ = S(x): |
|
|
|
|
|||||||||||||||||
5 |
5 |
x |
|
|
|
|
|||||||||||||||||||||||

x 7. ‚ëç¨á«¥-¨¥ -¥á®¡á⢥--ëå ¨-â¥£à «®¢ |
57 |
’ ª ª ª á㬬 |
- «¨â¨ç¥áª®£® ¯à®¤®«¦¥-¨ï ¯®«ãç¥--®£® |
|||||||||||||||||||||
àï¤ |
S(z) ¨ äã-ªæ¨ï f(z) |
ॣã«ïà-ë ¢ ª®«ìæ¥ fz : jzj > 2g, |
||||||||||||||||||||
¯à¨ç¥¬ f(x) = S(x) ¤«ï ¢á¥å x 2 R, |
|
x > 2, â® ¯® ⥮६¥ |
||||||||||||||||||||
¥¤¨-á⢥--®á⨠¤«ï ॣã«ïà-ëå äã-ªæ¨© |
3 |
|
1 |
ck |
||||||||||||||||||
|
|
|
|
|
|
|
|
e¡3¼i=5 |
|
|||||||||||||
|
f(z) = S(z) = e¡3¼i=5 ¡ |
|
|
|
|
|
|
¢ |
|
+ |
X |
|
|
|||||||||
|
|
|
z |
|
5 |
k=2 |
zk |
|||||||||||||||
¤«ï ¢á¥å z 2 C, jzj > 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
‘«¥¤®¢ ⥫ì-®, |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
res f(z) = |
c |
|
= |
|
e¡3¼i=5: |
|
(11) |
||||||||||||||
|
|
5 |
|
|||||||||||||||||||
|
z= |
1 |
|
¡ |
|
¡1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•¥à¥å®¤ï ª ¯à¥¤¥«ã ¢ à ¢¥-á⢥ |
(8) |
á ãç¥â®¬ á®®â-®è¥- |
||||||||||||||||||||
-¨© (9){(11), ¯®«ãç ¥¬ |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
I ³1 ¡ e¡6¼i=5 |
´ |
|
¼ie¡3¼i=5 |
|
|
|
|||||||||||||||
|
= |
|
|
|
|
|||||||||||||||||
¨«¨ |
5 |
|
|
|
||||||||||||||||||
|
|
à |
|
2i |
|
|
|
|
|
! |
|
|
|
5 |
|
|
|
|
|
|||
|
I |
|
e3¼i=5 |
¡ e¡3¼i=5 |
|
|
|
= |
3¼ |
; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
®âªã¤ - 室¨¬
I = |
3¼ |
|
|
: |
N |
5 sin |
3¼ |
|
|||
|
5 |
|
|
|
|
|
|
|
|
|
•à¨¬¥à. ‚ëç¨á«¨âì ¨-â¥£à «
|
|
|
I = |
Z0 |
(x + 1)(x + 2)2 dx: |
(12) |
|||||
|
|
|
|
+1 |
|
ln x |
|
|
|
||
|
•¥è¥-¨¥. |
‚ ª®¬¯«¥ªá-®© ¯«®áª®á⨠á à §à¥§®¬ ¯® «ãçã |
|||||||||
[0; +1) äã-ªæ¨ï h(z) = ln jzj + i', 0 < ' < 2¼ ï¥âáï ॣã- |
|||||||||||
«ïà-®© ¢¥â¢ìî ¬-®£®§- ç-®© äã-ªæ¨¨ Ln z (x 17). |
|
||||||||||
|
Ž¡®§- 稬 |
|
|
|
1 |
|
|
|
|
|
|
|
R(z) = |
|
|
|
|
; f(z) = R(z)h2(z) |
|
||||
|
|
|
|
|
|
|
|||||
|
(z + 1)(z + 2)2 |
|
|||||||||
|
|
|
|
|
|
|
|||||
¨ |
à áᬮâਬ |
®¡« áâì |
D, |
£à -¨æ |
¡ ª®â®à®© |
¯®ª § - |
|||||
- |
(à¨á. 7.5), £¤¥ 0 < ½ < 1, |
R > 2. |
‚ í⮩ ®¡« á⨠äã-ª- |
||||||||
æ¨ï f(z) ॣã«ïà- , § |
¨áª«îç¥-¨¥¬ â®ç¥ª z = ¡1, |
z = ¡2, |
|||||||||

58
CR
D C½ °+
¡2¡1 0 ½ °¡
•¨á. 7.5
¨ -¥¯à¥àë¢- ®ª®«® ¡ ¢¯«®âì ¤® ¡. •® ®á-®¢-®© ⥮६¥ ® ¢ë-
ç¥â å ¯®«ãç ¥¬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Z f(z) dz + Z |
f(z) dz +°Z f(z) dz + |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
C½ |
|
CR |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ °Z |
|
|
|
|
|
|
|
|
|
res |
|
|
|
res |
f(z) |
|
|
|
(13) |
|||
|
|
|
|
f(z) dz = 2¼i ·z=¡1 f(z) + z=¡2 |
¸: |
|
|
|
|
||||||||||||||||
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• áᬮâਬ ¯®®ç¥à¥¤-® ç«¥-ë í⮣® à ¢¥-á⢠. ’ ª ª ª |
|||||||||||||||||||||||
jh(z)j 6 j ln jzjj + 2¼, â® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
¯ |
Z |
f(z) dz¯ |
= |
¯ |
|
h2(z) dz |
|
|
¯ |
6 |
|
|
|
|
|
|
|
|
|
|
|
||||
(z + 1)(z + 2) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
¯ |
¯ |
|
¯ Z |
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
¯C½ |
¯ |
|
¯C½ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
¯ |
|
¯ |
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
||
¯ |
|
¯ |
|
¯ |
|
|
|
( |
|
|
¯ |
|
2 |
2¼½ |
|
|
|
|
|
|
|
|
|||
¯ |
|
¯ |
|
¯ |
|
|
|
ln ½¯ |
+ 2¼) |
|
|
|
|
|
|
|
|
||||||||
¯ |
|
¯ |
|
¯ |
6 |
j |
|
|
|
¯j |
|
|
|
|
! |
0 |
¯à¨ ½ |
! |
+0; |
||||||
|
|
(1 ¡ ½)(2 ¡ ½)2 |
|||||||||||||||||||||||
¯ |
Z |
f(z) dz¯ |
= |
¯ |
|
h2(z) dz |
|
|
|
¯ |
6 |
|
|
|
|
|
|
|
|
|
|
|
|||
(z + 1)(z + 2) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
¯ |
¯ |
|
¯ Z |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
¯CR |
¯ |
|
¯CR |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
¯ |
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
¯ |
|
¯ |
|
|
|
|
|
|
|
|
¯ |
2 |
2¼R |
|
|
|
|
|
|
|
|
||
¯ |
|
¯ |
|
¯ |
|
|
(ln R +¯ |
2¼) |
|
|
|
|
|
|
|
|
|||||||||
¯ |
|
¯ |
|
¯ |
6 |
|
|
|
|
|
|
¯ |
|
|
|
|
|
0 |
|
¯à¨ R |
|
|
+ : |
||
|
|
(R ¡ 1)(R ¡ 2)2 ! |
|
! |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||
|
|
…᫨ z 2 °+, â® h(z) = ln x, |
|
|
|
|
¥á«¨ z 2 °¡, â® h(z) = ln x + |
||||||||||||||||||
+ 2¼i. ’ ª ª ª á㬬 ¨-â¥£à «®¢ ¯® °+ ¨ °¡ ¢ «¥¢®© ç á⨠(13)
x 7. ‚ëç¨á«¥-¨¥ -¥á®¡á⢥--ëå ¨-â¥£à «®¢ |
59 |
à ¢-
R |
R |
|
|
|
|
Z½ |
ln2 x ¢ R(x) dx ¡ Z½ |
(ln x + 2¼i)2R(x) dx = |
Z½ |
R(x) dx; |
|
|
= ¡4¼i Z½ |
ln x ¢ R(x) dx + 4¼2 |
|||
|
|
R |
|
R |
|
â® ¯¥à¥å®¤ï ¢ «¥¢®© ç áâ¨ à ¢¥-á⢠(13) ª ¯à¥¤¥«ã ¯à¨ ½ ! +0, R ! +1, ¯®«ãç ¥¬ ¡4¼iI + 4¼2I1, £¤¥
+1 |
|
|
I1 = Z0 |
dx |
: |
|
||
(x + 1)(x + 2)2 |
|
• ©¤¥¬ §- ç¥-¨¥ ¯à ¢®© ç á⨠(13), ª®â®à ï -¥ § ¢¨á¨â ®â ½ |
||||||||||||||||||||||||||||||
¨ R. ’ ª ª ª z = ¡1 | ¯®«îá ¯¥à¢®£® ¯®à浪 , |
|
z = ¡2 | |
|||||||||||||||||||||||||||||
¯®«îá ¢â®à®£® ¯®à浪 |
|
äã-ªæ¨¨ f(z), â® |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
res f(z) = |
h2(z) |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
(z + 2)2 ¯z= 1 = (i¼) = ¡¼ ; |
|
|
|
||||||||||||||||||||||||
|
|
|
|
z=¡1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
¡ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
(z) |
0 |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
2 |
(z) |
|
|
|
|
|
|
|||
res f(z) = |
µ |
h |
¶ |
¯ |
|
|
= |
· |
¯2h(z) |
|
|
h |
|
|
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
z + 1 |
|
|
z(z + 1) ¡ |
(z + 1)2 |
|
|
|
|
||||||||||||||||||||||
z= |
¡ |
2 |
|
|
|
|
|
|
|
|
|
z= |
¡ |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
¯z=¡2 |
|
|
|
|
|
|
|
|
|
|
|
¸¯¯ |
|
|
||||||||||
|
|
|
= ln 2 + i¼ |
|
|
¯ |
2 + i¼) |
2 |
= ¼ |
2 |
+ ln 2 |
|
|
|
2 |
|
¯ |
|
|
2 ln 2): |
|||||||||||
|
|
|
¡ |
(ln¯ |
|
|
¡ |
ln 2 + i¼(1 |
¡ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|||||
|
ˆ§ à ¢¥-á⢠|
|
(13) á«¥¤ã¥â, çâ® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
¡4¼iI + 4¼2I1 = 2¼i ¡ln 2 ¡ ln2 2 + i¼(1 ¡ 2 ln 2)¢; |
|
|||||||||||||||||||||||||||
®âªã¤ |
- 室¨¬, ¯à¨à ¢-ï¢ ¤¥©á⢨⥫ì-ë¥ ¨ ¬-¨¬ë¥ ç á⨠¨ |
||||||||||||||||||||||||||||||
ãç¨âë¢ ï, çâ® I1 |
2 R, |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
I = |
(ln2 2 ¡ ln 2): |
|
|
|
|
|
|
|
|
|
N |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
60
x 8. Š®-ä®à¬-ë¥ ®â®¡à ¦¥-¨ï í«¥¬¥-â à-묨 äã-ªæ¨ï¬¨
‘¯à ¢®ç-ë¥ á¢¥¤¥-¨ï
1. ‘⥯¥-- ï äã-ªæ¨ï.
•ãáâì t 2 R. • áᬮâਬ - ®¡« á⨠G = C n [0; +1) äã-ª- æ¨î
w = jzjteit arg z; |
£¤¥ |
arg z 2 (0; 2¼): |
(1) |
|
•â äã-ªæ¨ï ॣã«ïà- |
- G. |
•à¨ç¥¬ ¯à¨ t 6= 0 äã-ª- |
||
æ¨ï (1) ®¤-®«¨áâ- - ®¡« á⨠D ½ G, ¥á«¨ D -¥ ᮤ¥à¦¨â ¤¢ãå |
||||
à §«¨ç-ëå â®ç¥ª z1; z2, â ª¨å, çâ® z2 = z1 ¢ e2¼ik=t, |
k 2 Z. |
|||
‚ ç áâ-®áâ¨, ¯à¨ t > 0 äã-ªæ¨ï (1) ®áãé¥á⢫ï¥â ª®-ä®à¬- |
||||
-®¥ ®â®¡à ¦¥-¨¥ 㣫®¢®© ®¡« á⨠G0;'0 = |
fz : jzj |
> 0; 0 < |
||
< arg z < '0g, £¤¥ '0 6 2¼, |
jtj'0 |
6 2¼; - |
㣫®¢ãî ®¡« áâì |
|
G0;t'0 (à¨á. 8.1). |
|
|
|
|
y |
|
|
'0 |
|
'1 |
0 |
x |
v |
|
t'0 |
|
|
t'1 |
0 |
u |
•¨á. 8.1
• ¯à¨¬¥à, äã-ªæ¨ï w = z2 ª®-ä®à¬-® ®â®¡à ¦ ¥â
1) |
¢¥àå-îî ¯®«ã¯«®áª®áâì fz : Im z > 0g - |
¯«®áª®áâì á à §- |
|
|
१®¬ C n [0; +1) (à¨á. 8.2); |
|
|
2) |
¯®«ãªà㣠fz : jzj < 1; Im z > 0g |
- |
ªà㣠á à §à¥§®¬ |
|
fw : jwj < 1g n [0; 1) (à¨á. 8.3); |
|
|
3) |
¯®«ã¯«®áª®áâì fz : Im z > a > 0g - |
¢-¥è-®áâì ¯ à ¡®«ë |
|
fw = u + iv : v2 > 4a2(u + a2)g (à¨á. 8.4).
2. •ªá¯®-¥-æ¨ «ì- ï äã-ªæ¨ï.
”ã-ªæ¨ï w = ez ®áãé¥á⢫ï¥â ª®-ä®à¬-®¥ ®â®¡à ¦¥-¨¥ ¢ ®¡« á⨠D ½ C ⮣¤ ¨ ⮫쪮 ⮣¤ , ª®£¤ D -¥ ᮤ¥à¦¨â
