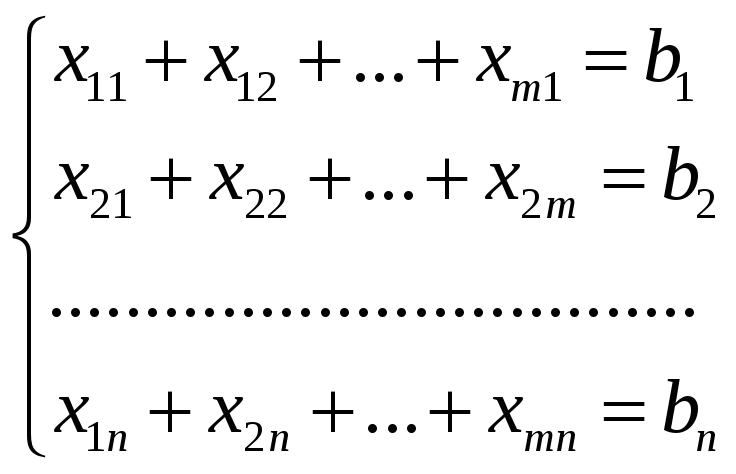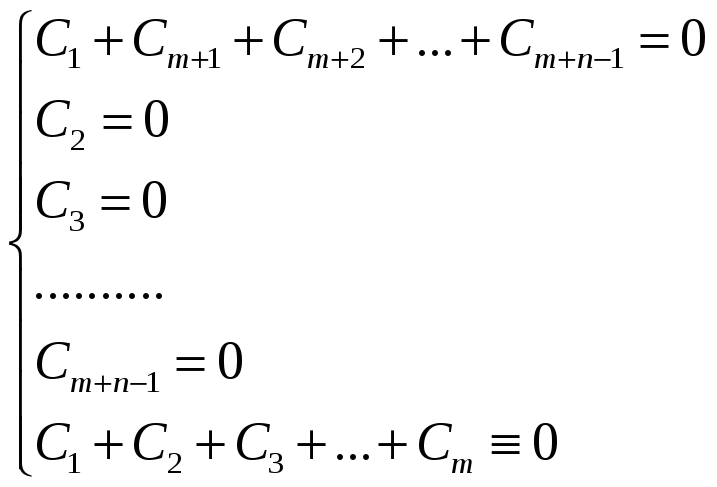Не разобранные / Линейное программирование / шпоры / 18-24

18. В m пунктах сосредоточен однородный груз в количествах Этот груз нужно перевезти n потребителям в количествах Известны числа - стоимость перевозки единицы груза от i-го поставщика j-му потребителю (тариф перевозки).Обозначим - объём груза, перевозимого от i-го поставщика j-му потребителю.

Условия транспортной задачи будем записывать в виде транспортной таблицы.

Введём вектор Х – план перевозок.План перевозок должен удовлетворять следующим условиям: грузы от каждого поставщика должны быть вывезены полностью, запросы каждого потребителя-полностью удовлетворены.

(1) (2)

Матем. формулировка ТЗ:

Найти такой план Х, удовлетворяющий системам ограничений (1) и (2), условиям неотрицательности (3) и обеспечивающий минимум целевой функции f.

19. Теорема о ранге системы векторов-условий транспортной задачи Ранг системы векторов условий транспортной задачи= (m+n-1).Док-во: Надо доказать, что max число линейно независимых векторов системы (*) равно (m+n-1).

Рассмотрим систему из (m+n-1) вектора:

(**)

Докажем:Система (**) линейно независима.

Составим лин комб-ю векторов системы (**).

Выясним,при каких знач. коэф-в вектор Y нулевой. 2 вектора равны тогда и только тогда, когда равны их соотв координаты

Система имеет единственное решение .Это означает, что только тривиальная лин комб системы векторов (**) равна θ сист векторов (**) л.н. Добавим в систему (**) вектор В рез-те получим следующую сист векторов

(+)

- нетривиальная линейная комбинация векторов - линейно зависимые вся система векторов (+) линейно зависима. Следствие:ранг(число базисных неизв в любом общем реш)= m+n-1

20. Отыскание исходного опорного решения транспортной задачи. Метод «северо-западного» угла. Метод минимальной стоимости.

Рассмотрим построение исходного опорного решения системы методом северо-западного угла.

Будем заполнять таблицу, начиная с клетки 11. Запишем в клетку 11

1му потребителю нужно ещё (b₁-a₁) единиц груза. Будем удовлетворять оставшиеся потребности 1 потребителя за счет запасов 2 поставщика. От 2 поставщика перевезём к 1 потребителю

(a₁-b₁) – у первого поставщика останется такое количество груза. Этими запасами 1 поставщика будет максимально удовлетворён 2 потребитель.

В клетку 12 запишем. Заполнив клетку 12 или клетку 21, двигаемся из неё в соседнюю клетку либо вправо по строке, если окажется закрыт соотв столбец, либо вниз по столбцу, если окажется закрытой соотв строка.И закрываем либо 1 столбец, либо 1 строчку для дальнейшего заполнения. Процесс продолжается до тех пор, пока не будут удовлетворены все запросы b_j и не исчерпаются все запасы a_i.Последняя заполняется клетка mn.

Может оказаться, что закроется одновременно i-я строка и k-й столбец, тогда занесём в соседнюю строчке или столбцу клетку, ту из них, которой соответствует наименьший тариф перевозки, запишем в ней 0. Такие 0, в отличие от 0 своб клеток, будем называть базисными 0.Метод минимальной стоимости Суть метода заключается в том, что из таблицы тарифов выбирают min, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i и b_j . Затем из рассмотрения исключают либо строку, соотв поставщику, запасы которого полностью израсходованы, либо столбец, соотв потребителю, потребности которого полностью удовлетворены, либо и строку и столбец. Процесс продолжают, пока все запасы не будут распред, а потребности удовл.

21Теорема: реш, построенное по методу СЗУ явл опорным. Док-во: достаточно доказать, что совокуп-ть заполн. клеток образует совокуп-ть базисных клеток. 1.Доказать: заполн-х клеток m+n-1. 2.Доказать:вектор-столбцы коэфф-в при неизв-х с номерами заполн-х клеток линейно незав.

1.На каждом этапе, кроме последнего, занесением очередного зн-я x_ik в табл закрывается только 1 столбец или 1 строка. И только в последней кл. одноврем. закрываются n-я строка и m-й столбец. Значит всего будет занесено в табл чисел x_ik на 1 меньше, чем имеется строк и столбцов.

2.Методом матем индукции по числу: k=2, (m=1, n=1)

b а	b1
a1	x11

Будет заполнена только 1 кл. x_11, и вектор b₁₁ образует линейно независимую сист . Предположение индукции: Пусть утверждение (2) выполн. при k=m+n-1. Докажем, что будет выполняться и при k=m+n. Будем заполнять таблицу методом СЗУ, и пусть для опред-сти x₁₁=a_11. 1я строчка закрыта, пусть будут заполнены (1,1), (2,1),…,(i,j),…,(m,n).Выпишем вектор-столбцы, соотв. клеткам с этими номерами.

(*) Докажем, что эти векторы лин. незав. Линейная комбинация:

У всех векторов системы (*), кроме вектора А₁₁ первые координаты равны нулю, т.к. у них первый индекс больше единицы.

С₁=0

(2)

Из исх. табл. вычеркнем 1 строчку и изменим потребности 1 потребителя на b₁-a₁. Получим новую ТЗ, у кот. число поставщиков равняется m-1, число потребителей n.Тогда k=m+n-1.Выпишем вектор-столбцы при неизв. с номерами заполненных кл.По предположению индукции эти векторы л.н.

Тогда в (1) получаем

22.Метод потенциалов. Теорема о достаточном условии оптимальности опорного решения транспортной задачи.

Т:Пусть Х₀ – опорное решение сист.огр-й (1),(2), - потенциалы.Если для каждой своб кл выпол усл-е: , то реш явл оптимальным.

Док-во:, пусть для допуст. реш.

[ - для любого решения выполняется условие (1) и(2)]

Для базисных клеток транспортной таблицы , а если клетка – свободная, то =0.Если имеется хотя бы одна свободная клетка, для которой не выполняется условие , то опорное решение не является оптим-м.

23. Переход от одного опорного решения к лучшему опорному решению. Сдвиг по циклу.

24. Алгоритм решения ТЗ методом потенциалов

1. Записываем исходн. опор. реш. в табл ТЗ.

2.Сопоставим каждому поставщику a_i число , а потребителю b_j - . Найдём эти неизв. из усл-я, что для кажд. базис. кл. выполн. усл.:

(Надо задать 1 неизвестное, а остальные находить из сист.) Всякое реш. сист. называется потенциалами данного опорного решения.

3.Если для кажд. своб. кл. выполн. усл.: , то реш. явл. оптимальным.

4.Если нет,то выбираем наибольш. оценку и строим цикл от кл. с этой оцен.

1.Формулировка и различные формы записи

задачи линейного программирования.

2.Переход от одной формы записи задачи к другой.

3.Графический метод решения задачи лин.прог.

4.Преобразование однократного замещения.

5.Опорные реш. Отыскание исходного опор. реш.

6.ОДР n-мерной задачи лин. прог.Гиперплоскость.

Полупространство. Выпуклые множества.

7.Т: пересеч. выпуклых множеств есть вып. мн.

8.Т: область реш. сист. лин. ур. и область реш.

системы лин. нер-в есть выпуклое множество.

9.Угловые т. выпуклого множества.Выпуклые многогр.

10.Теорема о существовании опорного решения.

11.Теорема о связи между угловыми т. ОДР задачи

линейного прог. и опорными решениями

12.Выпуклая линейная комбинация системы векторов.

Т. о совпадении множества точек ограниченного…

13.Основная теорема об экстремумах

14.Симплекс м.Теорема о возможности «улучшить» реш.

15.Симплекс м.: Критерий оптимальности опорного реш.

16.Симплекс м.: Т. об усл, при кот. задача не имеет реш.

17.Метод искусственного базиса. Теоремы о связи реш.

М-задачи и канонической задачи (формулировки).

18.Транспортная задача. Постановка, матем. формулир.

19.Теорема о ранге сист. векторов-условий ТЗ.

20.Отыскание исходного опорного решения ТЗ.

Метод СЗУ. Метод минимальной стоимости.

21.Т: решение, построенное по методу СЗУ явл. опорным.

22.Метод потенциалов. Т. о достаточном усл. оптимальности…

23.Переход от одного опорного решения к «лучшему»…

24.Алгоритм решения транспортной задачи методом потенциалов.

25Т. Если ОДР ЗЛП ограниченная, то опт реш существует и

совпадает хотя бы с 1 из опорных реш. системы огранич. ур-й.

26.Т. Если max линейной ф-и достигается в нескольких опорных

решениях Х1, Х2…,Хi, то любая выпуклая лин комб…