
- •Логвенков с.А., Мышкис п.А. Самовол в.С.
- •Предисловие.
- •1. Область определения, линии уровня функции нескольких переменных.
- •2.44. ,,.
- •3. Первый и второй дифференциал. Касательная плоскость.
- •4. Приближенные вычисления. Формула Тейлора.
- •5. Локальный экстремум функции нескольких переменных.
- •7. Двойной интеграл.
- •Библиографический список
7. Двойной интеграл.
Найдите
интеграл
![]() .
Сравните результат с объемом
соответствующего тела.
.
Сравните результат с объемом
соответствующего тела.
7.1.
![]() ,
,![]() .
.
7.2.
![]() ,
,![]() .
.
7.3.
![]() ,
,![]() .
.
7.4.
![]() ,
,![]() .
.
7.5.
![]() ,
,![]() .
.
7.6.
![]() ,
,![]() .
.
7.7.
![]() ,
,![]() .
.
7.8.
![]() ,
,![]() .
.
7.9.
![]() ,
,![]() .
.
7.10.
![]() ,
,![]() .
.
7.11.
![]() ,
,![]() .
.
7.12.
![]() ,
,![]() .
.
Изобразите
область
![]() и найдите интеграл
и найдите интеграл![]() .
Объясните совпадение ответов в пунктах
а и б.
.
Объясните совпадение ответов в пунктах
а и б.
7.13.
а)
![]() ,
,![]() .
.
б)
![]() ,
,![]() .
.
7.14.
а)
![]() ,
,![]() .
.
б)
![]() ,
,![]() .
.
7.15.
а)
![]() ,
,![]() .
.
б)
![]() ,
,![]() .
.
7.16.
а)
область D
ограничена
линиями![]() ,
,![]() ,
,![]() ,
,![]() .
.
б)
область D
ограничена
линиями
![]() ,
,![]() ,
,![]() ,
,![]()
7.17.
а)
область D
ограничена
линиями
![]() ,
,![]() ,
,![]() ,
,![]() .
.
б)
область D
ограничена
линиями
![]() ,
,![]() ,
,![]() ,
,![]()
Изобразите область интегрирования на плоскости. Измените порядок интегрирования в повторном интеграле
7.18.
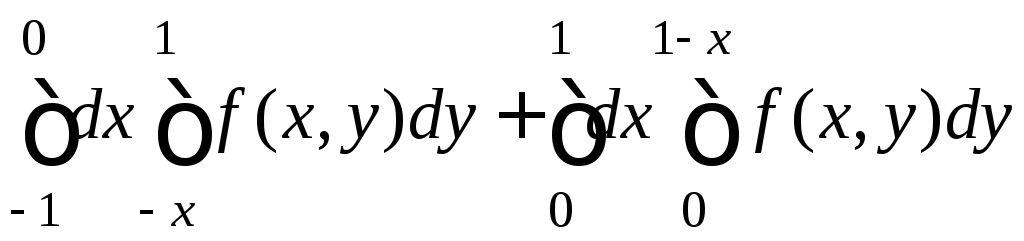 .
.
7.19.
 .
.
7.20.
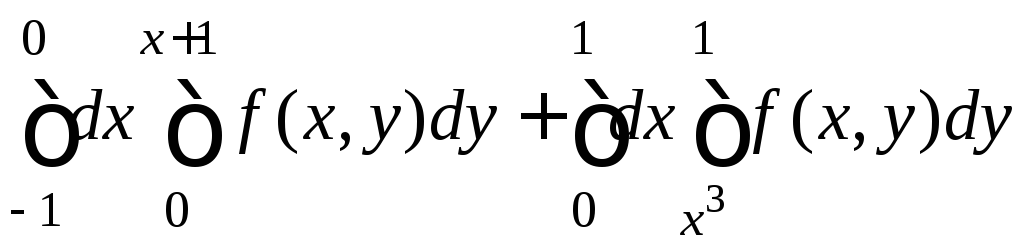 .
.
7.21.
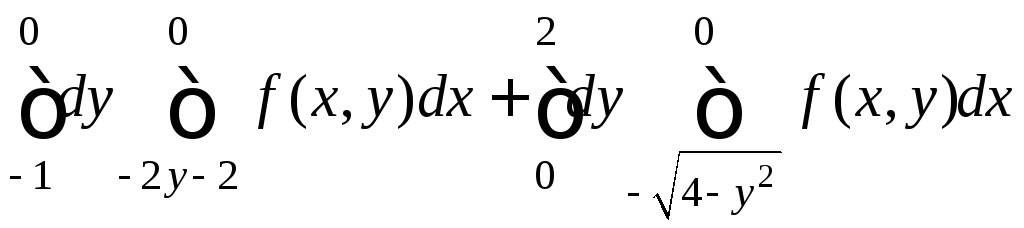 .
.
7.22.
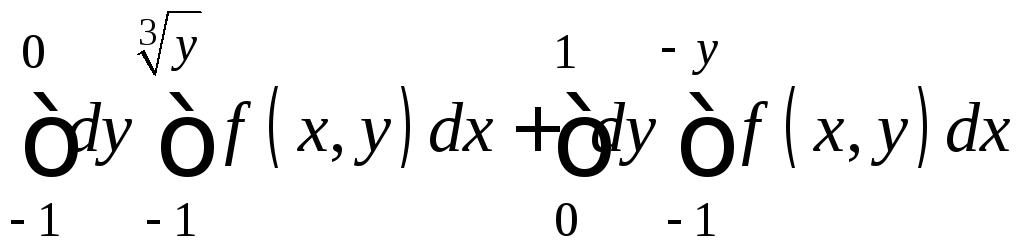
7.23.
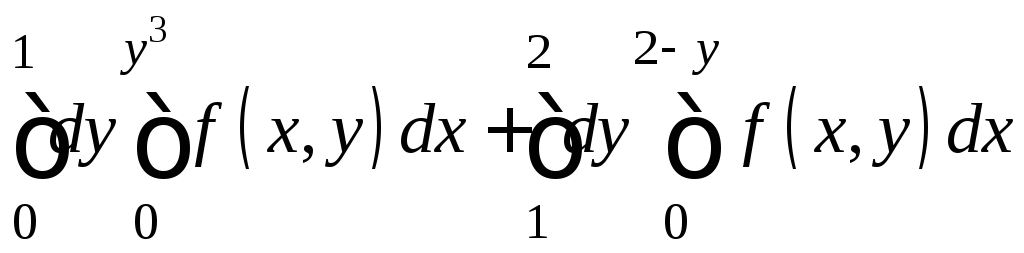
7.24.
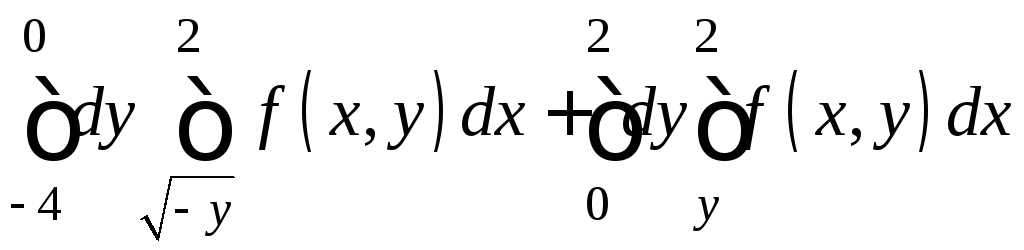
7.25.
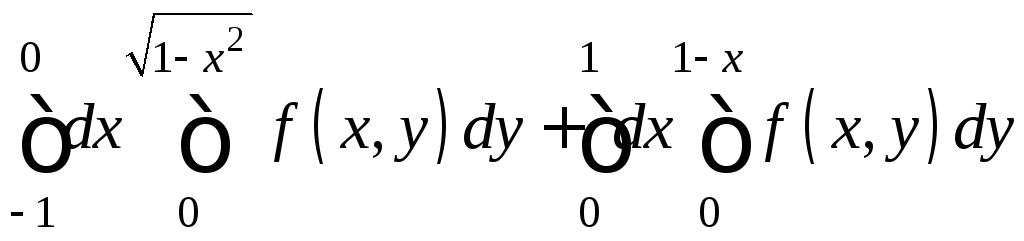
7.26.
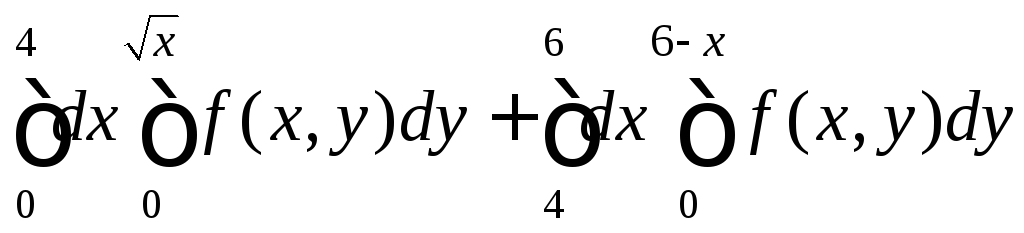
Изобразите область интегрирования на плоскости. Измените порядок интегрирования и найдите интеграл.
7.27.
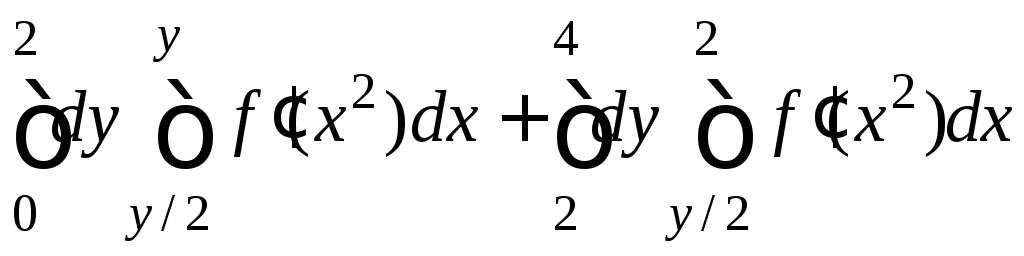 .
.
7.28.
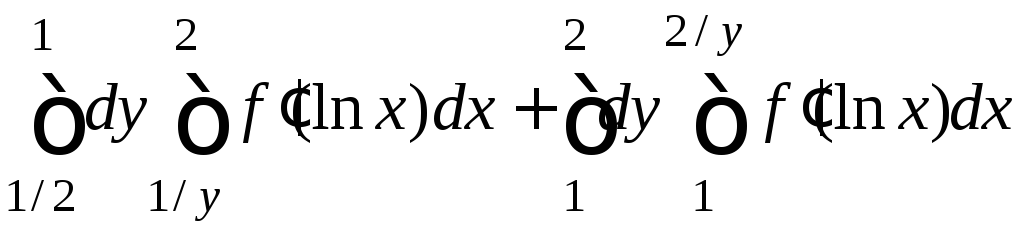 .
.
8. Дополнительные задачи.
8.1.
Найдите все
точки
![]() ,
для которых векторы
,
для которых векторы![]() и
и![]() коллинеарны и
коллинеарны и![]() ,
если задана точка
,
если задана точка![]() .
.
8.2.
Найдите время
![]() ,
необходимое для перехода из точки
,
необходимое для перехода из точки![]() в точку
в точку![]() объекта, движущегося со скоростью
объекта, движущегося со скоростью![]() .
.
8.3.
Объект, двигаясь
по плоскости последовательно со
скоростями
![]() и
и![]() ,
попадает из точки
,
попадает из точки![]() в точку
в точку![]() .
Найдите соответствующие временные
интервалы
.
Найдите соответствующие временные
интервалы![]() и
и![]() ,
а также точку
,
а также точку![]() смены скоростей
смены скоростей![]() на
на![]() .
.
8.4.
Объект, двигаясь
последовательно со скоростями
![]() ,
,![]() и
и![]() ,
попадает из точки
,
попадает из точки![]() в точку
в точку![]() .
Найдите соответствующие временные
интервалы
.
Найдите соответствующие временные
интервалы![]() ,
,![]() и
и![]() ,
а также точки
,
а также точки![]() и
и![]() смены скоростей
смены скоростей![]() на
на![]() и
и![]() на
на![]() .
.
8.5.
Найдите
величину параметра
![]() ,
если угол между векторами
,
если угол между векторами![]() и
и![]() равен
равен![]() .
.
8.6.
Найдите
величину параметра
![]() ,
если угол между векторами
,
если угол между векторами![]() и
и![]() равен
равен![]() .
.
8.7.
Найдите
величину параметра
![]() ,
если угол между векторами
,
если угол между векторами![]() и
и![]() равен
равен![]() .
.
8.8.
Найдите
величину параметра
![]() ,
если угол между векторами
,
если угол между векторами![]() и
и![]() равен
равен![]() .
.
8.9.
Найдите
косинус угла между вектором
![]() и вектором
и вектором![]() – проекцией вектора
– проекцией вектора![]() на координатную плоскостьxOy.
на координатную плоскостьxOy.
8.10. Найдите каноническое уравнение прямой, полученной отражением прямой
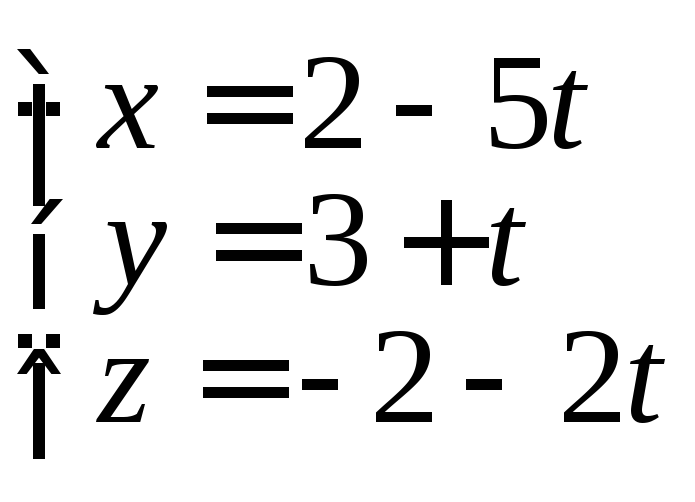 относительно
координатной плоскости yOz.
относительно
координатной плоскости yOz.
8.11.
Найдите
параметрическое уравнение прямой,
полученной отражением прямой
![]() относительно координатной осиOz.
относительно координатной осиOz.
8.12.
Найдите
уравнение плоскости, полученной
отражением плоскости
![]() относительно координатной плоскостиxOz.
относительно координатной плоскостиxOz.
8.13.
Найдите
уравнение плоскости, полученной
отражением плоскости
![]() относительно координатной осиOx.
относительно координатной осиOx.
8.14.
На прямой
![]() взяты две точкиA
и B
на расстоянии
взяты две точкиA
и B
на расстоянии
![]() друг от друга. На каком расстоянии друг
от друга лежат их проекции
друг от друга. На каком расстоянии друг
от друга лежат их проекции![]() и
и![]() на ось
на ось![]() ?
?
8.15. При каких значениях параметра x площадь параллелограмма, построенного на векторах (x; 3) и (3; 4), больше площади параллелограмма, построенного на векторах (2; 3) и (3; 4)?
8.16.
При каких
значениях параметра p
объем параллелепипеда, построенного
на векторах ![]() ,
,
![]() и
и ![]() меньше объема параллелепипеда,
построенного на векторах
меньше объема параллелепипеда,
построенного на векторах ![]() ,
,
![]() и
и ![]() ?
?
8.17.
Найдите
расстояние от сферы
![]() до точки
до точки![]() .
.
8.18.
Найдите
расстояние от сферы
![]() до сферы
до сферы![]() .
.
.
8.19.
Найдите
расстояние от сферы ![]() до сферы
до сферы ![]() .
.
8.20.
Найдите точку
![]() касания сфер
касания сфер ![]() и
и ![]() .
.
8.21.
Найдите точку
![]() касания сфер
касания сфер ![]() и
и ![]() .
.
8.22.
Найдите
расстояние от сферы
![]() до плоскости
до плоскости![]() .
.
8.23.
При каких значениях параметра
![]() плоскость
плоскость
![]() касается сферы
касается сферы![]() .
.
8.24.
Найдите радиус
r
окружности, по которой сфера
![]() пересекается с плоскостью
пересекается с плоскостью![]() .
.
8.25.
Дан бесконечный
конус с вершиной
![]() ,
осью {
,
осью {![]() ;
;![]() ;
;![]() ;
;![]() }
и углом при вершине
}
и углом при вершине![]() таким, что
таким, что![]() .Найдите
.Найдите
а) уравнение поверхности (боковой) этого конуса.
б) условие на координаты точек его внутренней части.
8.26.
Найдите
![]() ,
если
,
если .
(Указание: считайте матрицу
.
(Указание: считайте матрицу![]() матрицей коэффициентов систем линейных
уравнений, с соответствующими правыми
частями).
матрицей коэффициентов систем линейных
уравнений, с соответствующими правыми
частями).
8.27.
Исследовать совместность следующих
систем уравнений в зависимости от
параметра
![]()
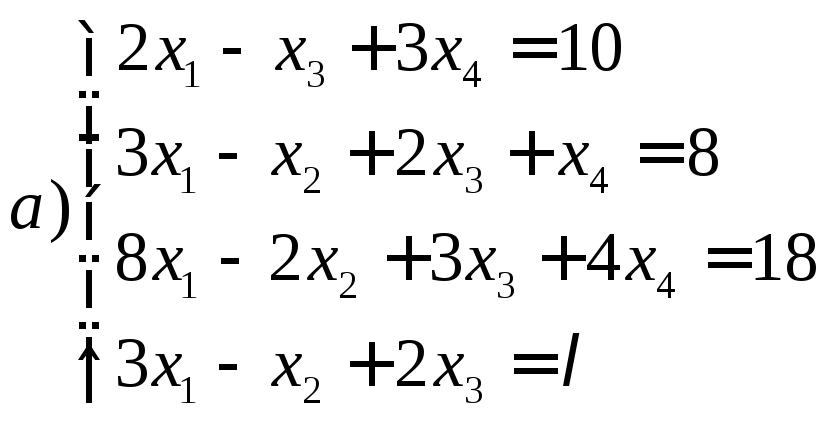
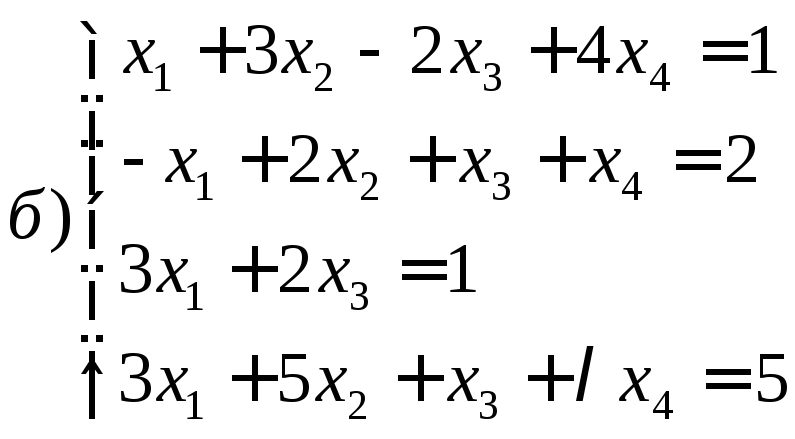
8.28.
Найдите ,
если
,
если![]() при
при![]() .
.
8.29.
Используя
только определение производной, действия
с ней и табличные производные, найдите
![]() .
.
8.30. Используя только определение производной, действия с ней и табличные производные, найдите xπ/4lim , если f(π/4) =2, f(1) = 3, f (π/4) = 4, f (1) = 5.
8.31. Используя только определение производной, действия с ней и табличные производные, найдите xπ/4lim , если f(π/4) =2, f(1) = 3, f (π/4) = 4, f (1) = 5.
8.32.
Найдите
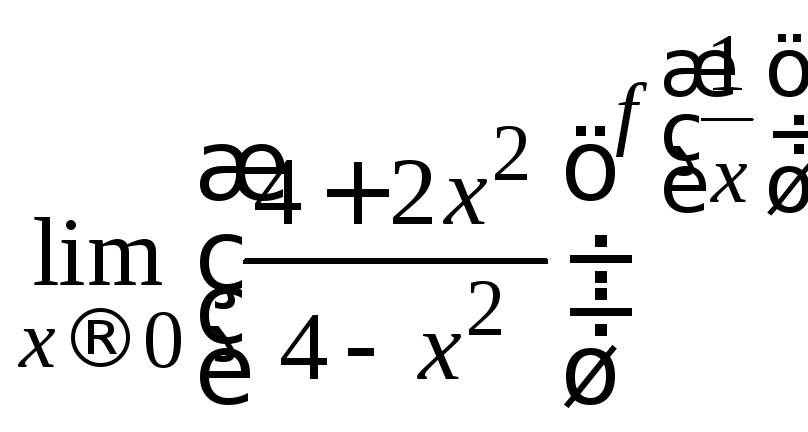 ,
если
,
если![]() при
при![]() .
.
8.33.
Дана эластичность
функции ![]() .
Найдите предел эластичности
.
Найдите предел эластичности
![]() при
при![]() ,
если
,
если![]() .
Сравните результат с эластичностью
.
Сравните результат с эластичностью![]() ,
где
,
где![]() при
при
![]() .
.
8.34.
Найдите предел
эластичности
![]() при
при![]() ,
если
,
если![]() .
Сравните результат с эластичностью
.
Сравните результат с эластичностью![]() ,
где
,
где![]() при
при
![]() .
.
8.35.
Известно, что
![]() ,
,![]() и
и![]() .
Чему равно значение
.
Чему равно значение![]() ?
?
8.36.
Известно, что
![]() ,
,![]() ,
,![]() и
и![]() .
Чему равно значение
.
Чему равно значение![]() ?
?
8.37.
Найдите
![]() ,
если
,
если![]() ,
где
,
где![]() .
.
8.38.
Найдите
![]() ,
если
,
если![]() ,
где
,
где![]() .
.
8.39.
Вычислите
дробь
![]() ,
еслиh(x)
= g(3x).
,
еслиh(x)
= g(3x).
8.40.
Вычислите
дробь
![]() ,
еслиg(x)
= ln
h(x).
,
еслиg(x)
= ln
h(x).
8.41.
Зависимость
![]() от
от![]() задана параметрически, причем
задана параметрически, причем![]() и
и![]() .
Найдите
.
Найдите![]() при
при![]() .
.
8.42.
Зависимость
![]() от
от![]() задана параметрически, причем
задана параметрически, причем![]() и
и![]() .
Найдите
.
Найдите![]() при
при![]() .
.
8.43. К графику функции y = 0,5 (x – 2)6 в точке M(3; 0,5) проведена касательная. На касательной взяты точки A и B с разностью проекций на ось Ox равной 5.
а)Найдите разность их проекций на ось Oy.
б) Найдите квадрат расстояния между точками A и B.
в) Найдите тангенс угла наклона касательной к оси Ox при выборе разного масштаба на координатных осях: |OB| = |OA|, если A(20,0), B(0,30).
8.44. Прямая l получена зеркальным отражением касательной из предыдущей задачи относительно прямой y = x. Найдите квадрат расстояния между точками A и B, находящимися на прямой l, если разность их проекций на ось Ox равна 6.
8.45.
Зависимость
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найдите параметр
.
Найдите параметр![]() в уравнении
в уравнении![]() касательной к графику
касательной к графику![]() в точке
в точке![]() ,
если
,
если![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
8.46.
Найдите
точку минимума функции
![]() ,
если
,
если![]() – монотонно убывающая функция, не
имеющая критических точек.
– монотонно убывающая функция, не
имеющая критических точек.
8.47.
Найдите
точку максимума функции
![]() ,
если
,
если![]() – монотонно убывающая функция, не
имеющая критических точек.
– монотонно убывающая функция, не
имеющая критических точек.
8.48. Найдите множество всех возможных значений f(180), если
f(0) = 0 и 1 ≤ f (x) ≤ 2 при всех x[0; 180].
8.49. Найдите множество всех возможных значений f(180), если f(400) = 500 и 1 ≤ f (x) ≤ 2 при всех x[180; 400].
8.50. Найдите множество всех возможных значений f(180), если f(0) = 0, f(400) = 500 и 1 ≤ f (x) ≤ 2 при всех x[0; 400].
8.51.
Найдите
сумму ординат всех точек пересечения
асимптот графика
![]() .
.
.
8.52.
Найдите
сумму ординат всех точек пересечения
асимптот графика
![]() .
.
8.53. Найдите множество всех возможных значений f(2), если f(0) = 0, f (0) = 1 и 1 ≤f (x) ≤ 6x2+ 1 при всехx[0; 2].
8.54.
Функция
![]() определена и имеет непрерывную вторую
производную при всех
определена и имеет непрерывную вторую
производную при всех![]() .
График функции
.
График функции![]() имеет асимптоту
имеет асимптоту![]() при
при![]() и
и![]() при
при![]() .
Кроме того,
.
Кроме того,
![]() при всех
при всех
![]() .
Изобразите эскиз графика
.
Изобразите эскиз графика![]() и оцените возможные значения
и оцените возможные значения![]() .
.
8.55.
Функция
![]() определена и имеет непрерывную вторую
производную при всех
определена и имеет непрерывную вторую
производную при всех![]() .
График функции
.
График функции![]() имеет асимптоту
имеет асимптоту![]() при
при![]() и
и![]() при
при![]() .
Кроме того,
.
Кроме того,![]() при всех
при всех![]() .
Изобразите эскиз графика
.
Изобразите эскиз графика![]() и оцените возможные значения
и оцените возможные значения![]() .
.
8.56.
Напишите
разложение многочлена четвертой степени
![]() по степеням
по степеням![]() ,
используя формулу Тейлора. Найдите
,
используя формулу Тейлора. Найдите![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() .
.
8.57.
Напишите
разложение многочлена четвертой степени
![]() по степеням
по степеням![]() ,
используя формулу Тейлора. Найдите
,
используя формулу Тейлора. Найдите![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() .
.
8.58.
Используя
стандартные разложения функций
![]() ,
,![]() ,
,![]() по формуле Маклорена по степеням
по формуле Маклорена по степеням![]() ,
найдите наклонные асимптоты следующих
функций
,
найдите наклонные асимптоты следующих
функций
а)
![]()
б)
![]()
в)
![]()
8.59.
Вычислив производную
![]() ,
найдите
,
найдите![]() .
.
8.60.
Вычислив производную
![]() ,
найдите
,
найдите![]() .
.
8.61.
Известно, что
![]() и
и![]() .Найдите
.Найдите
![]() .
.
8.62.
Известно, что
![]() и
и![]() .Найдите
.Найдите
![]() .
.
8.63.
Известно, что
![]() и
и![]() – первообразная функции
– первообразная функции![]() .
Найдите
.
Найдите![]() ,
если
,
если![]() ,
,![]() и
и![]() .
.
8.64.
Известно, что
![]() и
и![]() – первообразная функции
– первообразная функции![]() .
Найдите
.
Найдите![]() ,
если
,
если![]() ,
,![]() и
и![]() .
.
8.65.
Известно, что
![]() и
и![]() .
Найдите
.
Найдите![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
8.66.
Известно, что
![]() и
и
![]() .
Найдите
.
Найдите
![]() ,
если
,
если![]() ,
,![]() ,
,![]() .
.
8.67.
Известно, что
![]() ,
где
,
где![]() – первообразная функции
– первообразная функции![]() .
Найдитеa,
b,
c,
d,
если
.
Найдитеa,
b,
c,
d,
если
![]() .
.
8.68.
Выразите через определенный интеграл
и найдите
![]() ,
если
,
если![]() ,
а функция
,
а функция![]() имеет непрерывную первую производную
и
имеет непрерывную первую производную
и![]() при
при![]() .
.
8.69.
Выразите через определенный интеграл
и найдите
![]() .
.
8.70.
Выразите через определенный интеграл
и найдите
![]() .
.
8.71.
Функция
![]() непрерывна и монотонно возрастает на
отрезке
непрерывна и монотонно возрастает на
отрезке![]() .
Найдите интервал
.
Найдите интервал![]() возможных значений
возможных значений![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Укажите графически функцию
.
Укажите графически функцию![]() так, чтобы:
так, чтобы:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.72.
Функция
![]() непрерывна и монотонно убывает на
отрезке
непрерывна и монотонно убывает на
отрезке![]() .
Найдите интервал
.
Найдите интервал![]() возможных значений
возможных значений![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Укажите графически функцию
.
Укажите графически функцию![]() так, чтобы:
так, чтобы:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.73.
Найдите
экстремумы функции
![]() (g(x)
– непрерывная функция).
(g(x)
– непрерывная функция).
8.74.
Известно, что
![]() – непрерывная функция,
– непрерывная функция,![]() ,
,![]() ,
,![]() и
и![]() .Найдите
g(0).
.Найдите
g(0).
8.75.
Известно, что
![]() – непрерывная функция,
– непрерывная функция,![]() ,
,![]() ,
, и
и![]() .Найдите
g(2).
.Найдите
g(2).
8.76.
Известно, что
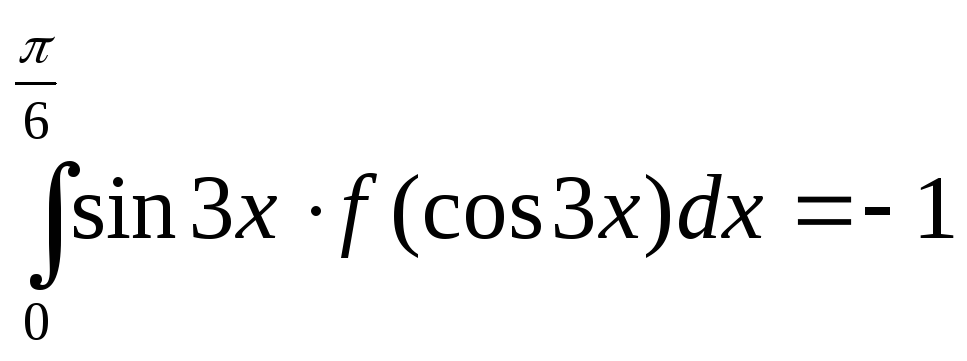 .
Найдите
.
Найдите![]() .
.
8.77.
Известно, что
![]() .
Найдите
.
Найдите![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() .
.
8.78.
Известно, что
![]() .
Найдите
.
Найдите
 ,
если
,
если
![]() ,
,![]() .
.
8.79.
Найдите
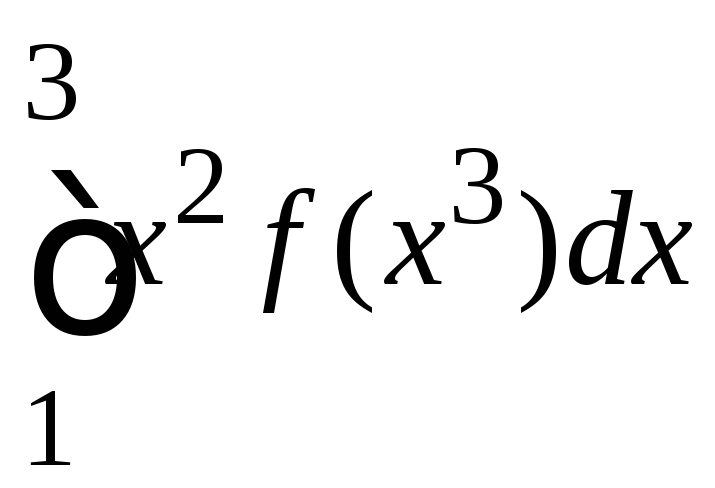 ,
если
,
если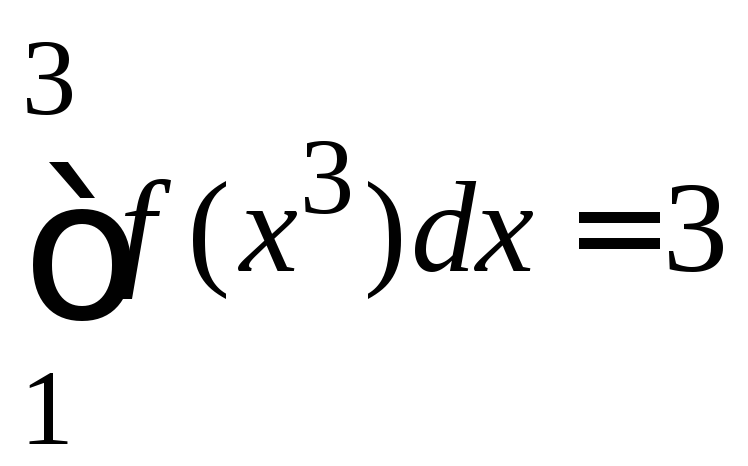 ,
,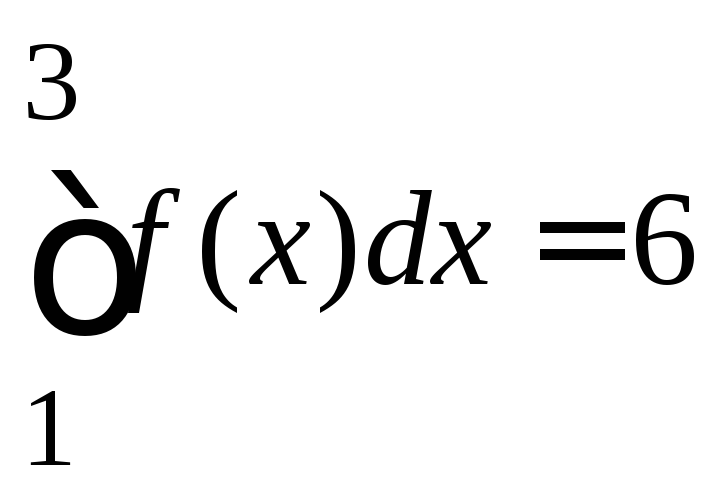 и
и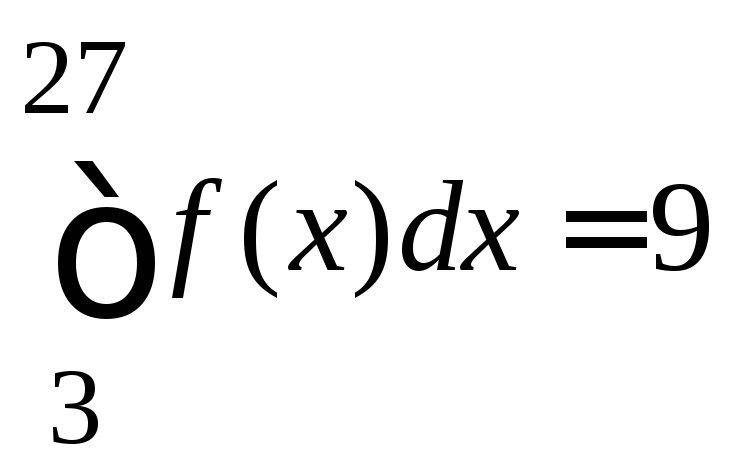 .
.
8.80.
Найдите
 ,
если
,
если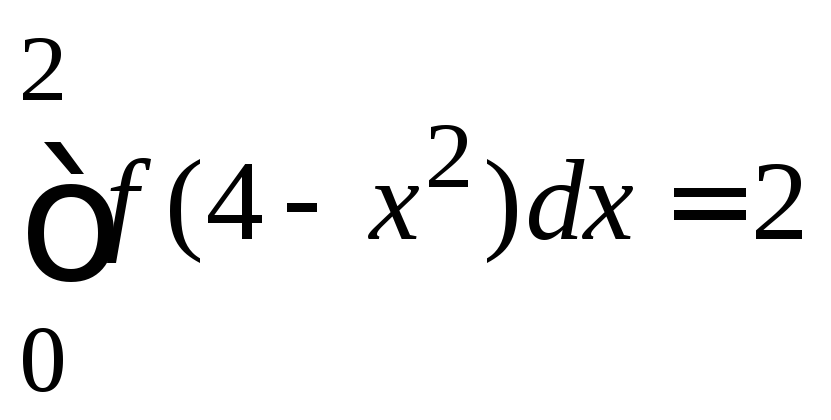 ,
,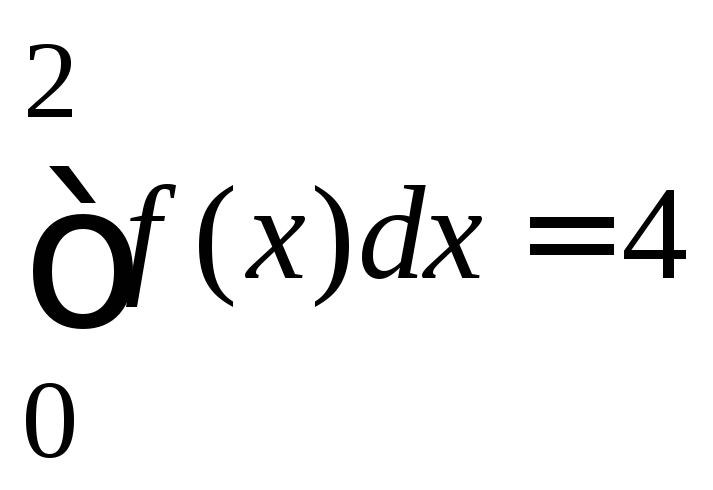 и
и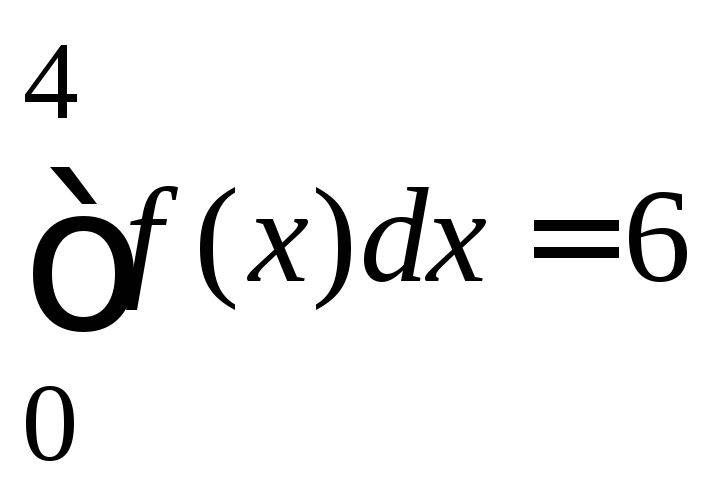 .
.
8.81.
Найдите определенный интеграл
 ,
если
,
если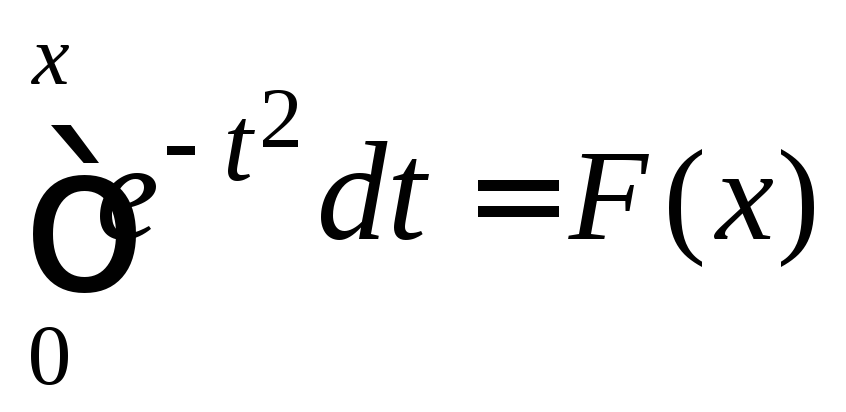 ,
где
,
где![]() – заданная функция.
– заданная функция.
8.82.
Известно, что
![]() ,
где
,
где![]() и
и![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
Найдите параметр
![]() ,
если
,
если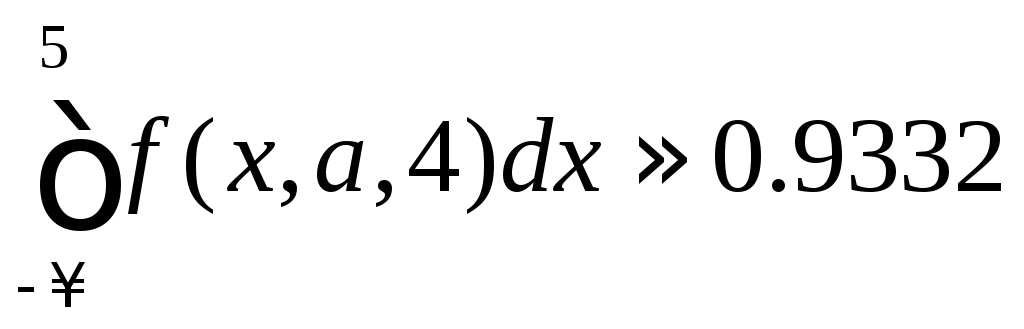 .
.
б)
Найдите параметр
![]() ,
если
,
если![]() .
.
в)
Найдите параметр
![]() ,
если
,
если![]() .
.
г)
Найдите параметр
![]() ,
если
,
если![]() .
.
8.83.
Пусть функция
![]() дифференцируема. Докажите, что
дифференцируема. Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.84.
Пусть функция
![]() дифференцируема и
дифференцируема и![]() .
Докажите, что
.
Докажите, что
![]() при
при![]() (
(![]() ).
Найдите
).
Найдите![]() .
.
8.85.
Известно,
что
![]() при
при![]() (
(![]() ,
,
![]() ).
Докажите, что функция
).
Докажите, что функция![]() дифференцируема и найдите
дифференцируема и найдите![]() .
.
8.86.
Пусть функция
![]() дифференцируема. Докажите, что
дифференцируема. Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.87.
Пусть функция
![]() дифференцируема, и все ее частные
производные первого порядка положительны.
Докажите, что
дифференцируема, и все ее частные
производные первого порядка положительны.
Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.88.
Пусть функция
![]() дифференцируема. Докажите, что
дифференцируема. Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.89.
Пусть функция
![]() дифференцируема, и все ее частные
производные первого порядка отрицательны.
Докажите, что
дифференцируема, и все ее частные
производные первого порядка отрицательны.
Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.90.
Используя
определение дифференциала, найдите
частные производные
![]() и
и![]() ,
если
,
если![]() и
и![]() .
.
8.91.
Дана
дифференцируемая функция двух переменных
![]() .
Известно, что
.
Известно, что![]() ,
,![]() ,
,![]() ,
где А(2; 6),B(2.03;
6,02), C(2,02;
5.97). Заменяя приращение функции
дифференциалом, найдите приближенно
частные производные точке в A.
,
где А(2; 6),B(2.03;
6,02), C(2,02;
5.97). Заменяя приращение функции
дифференциалом, найдите приближенно
частные производные точке в A.
8.92.
Пусть функция
![]() имеет непрерывные частные производные
2-го порядка в точке
имеет непрерывные частные производные
2-го порядка в точке![]() ,
и
,
и![]() .
Докажите, что
.
Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.93.
Пусть функция
![]() имеет положительные непрерывные частные
производные 2-го порядка в точке
имеет положительные непрерывные частные
производные 2-го порядка в точке![]() ,
и
,
и![]() .
Докажите, что
.
Докажите, что![]() при
при![]() и найдите
и найдите![]() .
.
8.94.
Функция
![]() имеет отрицательные непрерывные частные
производные 2-го порядка в точке
имеет отрицательные непрерывные частные
производные 2-го порядка в точке![]() ,
и
,
и![]() .
Докажите, что функция
.
Докажите, что функция![]() имеет локальный максимум при
имеет локальный максимум при![]() .
.
8.95.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.96.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.97.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.98.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.99.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.100.
Известно,
что
![]() при
при![]() .
Найдите производную функции
.
Найдите производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
8.101.
Найдите производную функции
![]() ,
по направлению
,
по направлению![]() в точке
в точке
![]() ,
если
,
если![]() .
.
8.102.
Найдите производную функции
![]() ,
по направлению
,
по направлению![]() в точке
в точке
![]() ,
если
,
если![]() .
.
8.103.
Градиент функции
![]() задан на оси
задан на оси![]() :
:![]() .
Найдите в точках оси
.
Найдите в точках оси![]() производные функции
производные функции![]() по направлению оси
по направлению оси![]() и исследуйте функцию
и исследуйте функцию![]() на условный экстремум на линии условия
на условный экстремум на линии условия![]() .
.
8.104.
Градиент функции
![]() задан на оси
задан на оси![]() :
:![]() .
Найдите в точках оси
.
Найдите в точках оси![]() производные функции
производные функции![]() по направлению оси
по направлению оси![]() и исследуйте функцию
и исследуйте функцию![]() на условный экстремум на линии условия
на условный экстремум на линии условия![]() .
.
8.105. Исследуйте, используя “окаймленный” гессиан, точку A на условный экстремум, если в этой точке первый дифференциал функции Лагранжа L(A,λ) равен нулю, а второй: d 2 L(A,λ) = 7(dx)2 – 4dxdy – 5(dy)2 – 2dxdλ+ 6dydλ.
8.106. Исследуйте точку A на условный экстремум, если в этой точке первый дифференциал функции Лагранжа L(A,λ) равен нулю, а второй:
d 2 L(A,λ) = 2(dx)2 – 20dxdy – 5(dy)2 + 4dxdλ – 10dydλ.
8.107. На линии условия φ(x; y) = 2x + y – 1 = 0 в семи точках даны градиенты функции двух переменных f(P) = f(x; y): в точке A(-3;7) градиент равен (3;1), в точке B(-2;5) – (2;1), в C(-1;3) – (3;1), в D(0;1) – (4;2), в E(1;-1) – (1;1), в F(2;-3) – (6;3), в G(3;-5) – (3;1). Все точки “подозрительные” на условный экстремум находятся среди указанных. Найдите эти точки и исследовать их на условный экстремум.
Найдитеобщее решение дифференциального уравнения с разделяющимися переменными
8.108.
а)
![]()
б)
![]()
в)
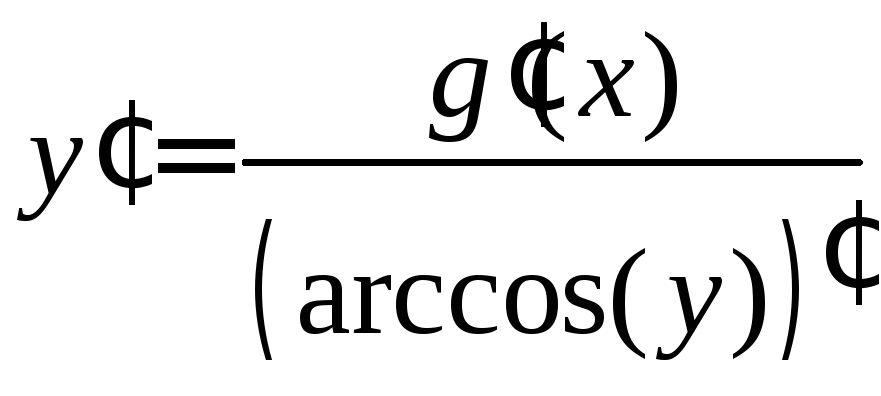
г)
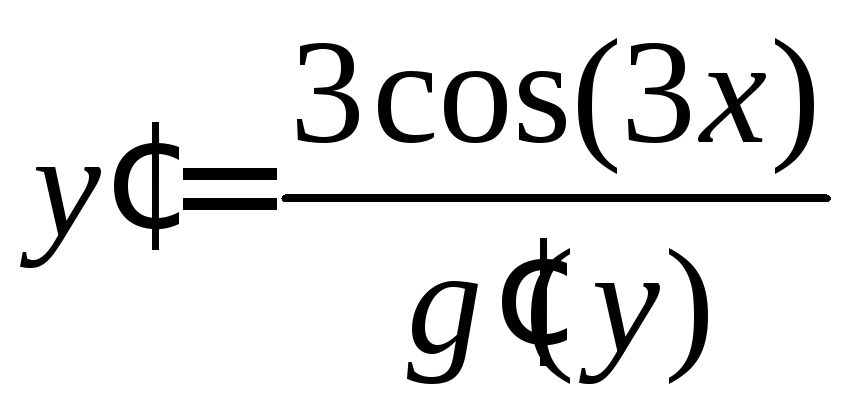 ,
если из соотношения
,
если из соотношения
![]() следует, что
следует, что![]()
Решите задачу Коши
8.109.
а)
![]() ,
,
![]() ,
если
,
если![]() .
.
б)
![]() ,
,
![]() ,
если
,
если![]() ,
,![]() .
.
в)
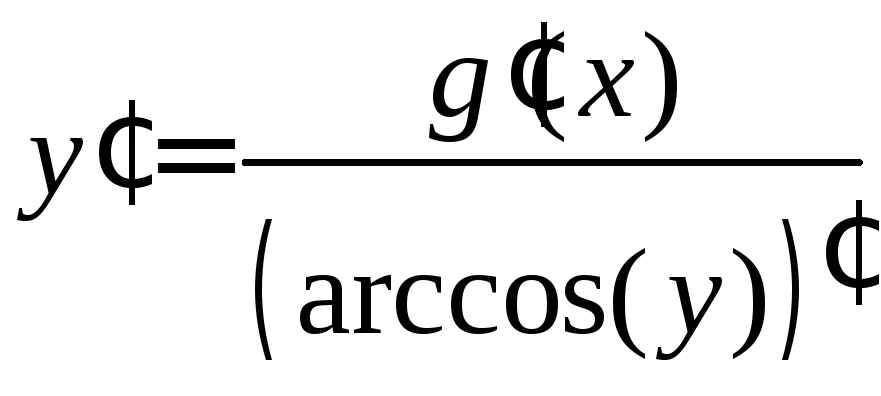 ,
,
![]() ,
если
,
если ![]() .
.
8.110.
Найдите общее решение однородного
дифференциального уравнения
 ,
если
,
если
а)
![]()
б)
![]()
8.111.
Проверьте, что общее решение
![]() линейного дифференциального уравнения
линейного дифференциального уравнения![]() имеет вид
имеет вид![]() ,
где
,
где![]() – частное решение исходного уравнения,
а
– частное решение исходного уравнения,
а![]() – общее решение уравнения
– общее решение уравнения![]() .
.
8.112.
Используя результат предыдущей задачи,
найдите общее решение
![]() линейного дифференциального уравнения
линейного дифференциального уравнения
а)
![]()
б)
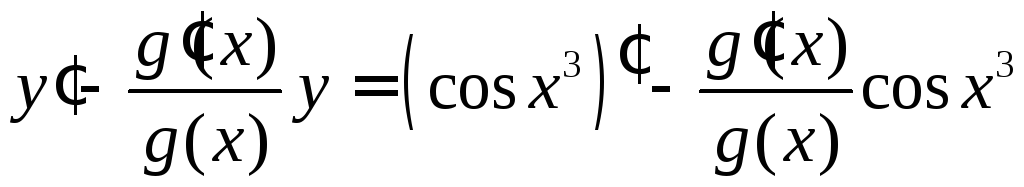
8.113.
При каких значениях ![]() и
и ![]() функция
функция ![]() является общим
решением уравнения
является общим
решением уравнения ![]() ?
?
8.114.
Найдите общее решение
![]() линейного дифференциального уравнения
второго порядка
линейного дифференциального уравнения
второго порядка![]()
8.115.
Найдите решение задачи Коши:
![]() ,
,![]() ,
,![]() ,
если
,
если![]() .
.
