
- •4.1. Формы представления задач линейного программирования
- •4.2. Структура допустимого множества и типы решений
- •Пример 1
- •4.3. Прямая и двойственная задачи. Теоремы двойственности. Экономическая интерпретация двойственных задач
- •Теорема о существовании решений
- •Теорема о совпадении оптимальных значений
- •Теорема о дополняющей нежесткости
- •Прямая задача
- •Двойственная задача
- •4.4. Графический метод решения задач линейного программирования
- •Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задача 4(см. Рис. 4.12)
- •Задача 4(см. Рис. 4.13)
- •4.5. Анализ чувствительности оптимального решения к параметрам задачи линейного программирования
- •Задача 1
- •4.6. Принцип гарантированного результата в задачах линейного программирования
- •4.7. Решение задач линейного программирования симплекс-методом
- •4.8. Транспортные задачи линейного программирования
- •2) Отчет по пределам (рис.16)
Теорема о существовании решений
Задача линейного программирования вида (4.4) или (4.5) имеет решение тогда и только тогда, когда допустимые множества прямой и двойственной задачи оба не пусты.
Действительно, если в прямой задаче допустимое множество пусто, то условие Куна-Таккера не выполняется ни при каких значениях х иу, а значит, и не может быть оптимума ни в одной из задач.
Обратно, если оба допустимых множества
не пусты, то существуют допустимые точки
![]() и
и![]() ,
причем для любых допустимых точекх
иу:
,
причем для любых допустимых точекх
иу:![]()
![]() и
и![]()
![]() ,
т.е. максимизируемая функция
,
т.е. максимизируемая функция![]() ограничена сверху, а минимизируемая
(
ограничена сверху, а минимизируемая
(![]() )
– снизу. Ввиду линейности функций и
замкнутости допустимых множеств отсюда
следует наличие глобальных оптимумов.
)
– снизу. Ввиду линейности функций и
замкнутости допустимых множеств отсюда
следует наличие глобальных оптимумов.
Теорема о совпадении оптимальных значений
Допустимые векторы х иуявляются
решениями задач (4.4) и (4.5) тогда и только
тогда, когда значения целевых функций
обеих задач на этих векторах совпадают:![]()
![]() .
.
Это утверждение непосредственно следует из неравенства (4.9) и условия задач (4.4) и (4.5) – требований максимизации и минимизации целевых функций.
Теорема о дополняющей нежесткости
Допустимые векторы х иуявляются решениями задач (4.4) и (4.5) тогда и только тогда, когда они удовлетворяют условиям дополняющей нежесткости:
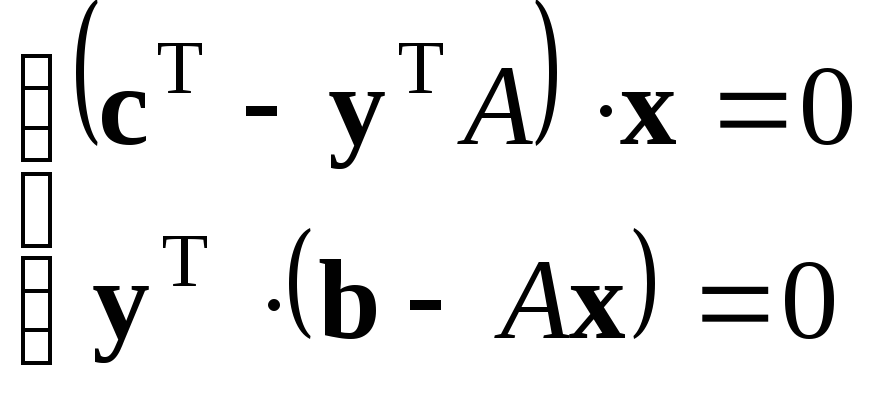 .
(4.11)
.
(4.11)
Это утверждения вытекает из предыдущей теоремы и системы условий (4.10).
Ввиду практической важности последней теоремы для решения задач графическим способом рассмотрим условия (4.8) подробнее. Для этого представим их в скалярной форме:
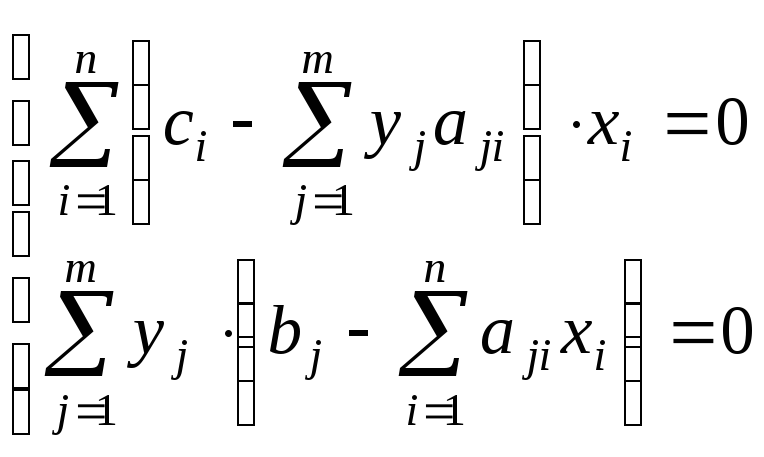 (4.12)
(4.12)
Поскольку мы рассматриваем только
допустимые точки, то
![]() и
и![]() ,
,![]() а
значит
а
значит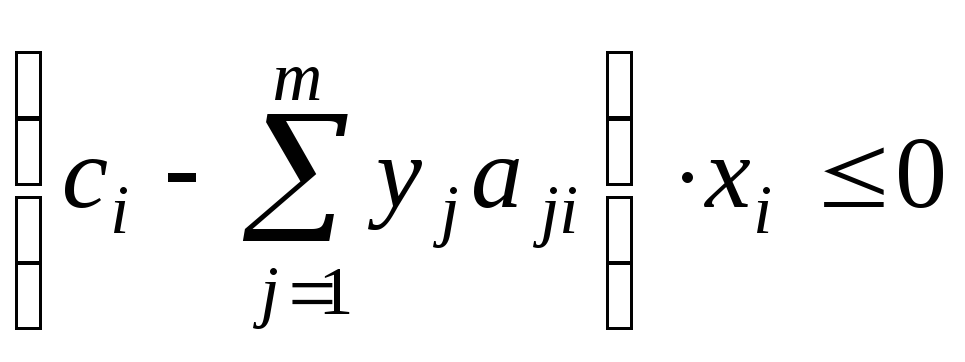 ,
,![]() т.е.
каждое слагаемое в первом неравенстве
(4.12) неположительно. Однако сумма их
равна нулю. Очевидно, это возможно только
при равенстве нулю каждого слагаемого.
Таким образом,
т.е.
каждое слагаемое в первом неравенстве
(4.12) неположительно. Однако сумма их
равна нулю. Очевидно, это возможно только
при равенстве нулю каждого слагаемого.
Таким образом, ,
,![]() а это, в свою очередь, означает, что в
каждом таком произведении хотя бы один
из сомножителей равен нулю.
а это, в свою очередь, означает, что в
каждом таком произведении хотя бы один
из сомножителей равен нулю.
Иными словами, можно сказать, что если
в оптимальной точке (прямой задачи)
![]() ,
то
,
то![]() ,
или, что то же самое,
,
или, что то же самое,![]() ,
т.е. соответствующее ограничение в
оптимальной точке двойственной задачи
превращается в равенство (активно). И
наоборот, если в оптимальной точке
двойственной задачи
,
т.е. соответствующее ограничение в
оптимальной точке двойственной задачи
превращается в равенство (активно). И
наоборот, если в оптимальной точке
двойственной задачи![]() ,
т.е. некоторое ограничение не активно,
то соответствующая переменная в
оптимальной точке прямой задаче равна
нулю:
,
т.е. некоторое ограничение не активно,
то соответствующая переменная в
оптимальной точке прямой задаче равна
нулю:![]() .
.
Аналогичные рассуждения справедливы относительно второго равенства из (4.12) с той лишь разницей, что там все сомножители неотрицательны.
Суммируя сказанное, теорему о дополняющей нежесткости можно сформулировать следующим образом:
10 Если в оптимальной точке прямой задачи некоторое ограничение не активно (неравенство выполняется строго), то в оптимальной точке двойственной задачи соответствующая переменная равна нулю.
20 Если в прямой задаче некоторая переменная не равна нулю (строго положительна), то в оптимальной точке двойственной задачи соответствующее ограничение обращается в равенство (активно).
Напомним, что понятия прямой и двойственной задач относительны: любую из взаимно двойственных задач можно считать прямой, тогда другая будет двойственной к ней.
Двойственные задачи допускают следующую экономическую интерпретацию.
Будем называть прямой задачей задачу на максимум вида (4.4), а двойственной – задачу на минимум вида (4.5).
