69

Тема 4

Линейное программирование

Формы представления задач линейного программирования. Структура допустимого множества и типы решений. Прямая и двойственная задачи. Теоремы двойственности. Экономическая интерпретация двойственных задач. Графический метод решения задач линейного программирования. Анализ чувствительности оптимального решения к параметрам задачи линейного программирования. Принцип гарантированного результата в задачах линейного программирования. Решение задач линейного программирования симплекс-методом. Транспортные задачи линейного программирования. Компьютерная реализация решения задач линейного программирования

4.1. Формы представления задач линейного программирования

Задачи линейного программирования являются разновидностью задач математического программирования. В задачах линейного программирования допустимая область задается в виде системы неравенств и/или равенств, причем все функции в этих ограничениях, а также целевая функция линейны:

, или, в векторной форме:,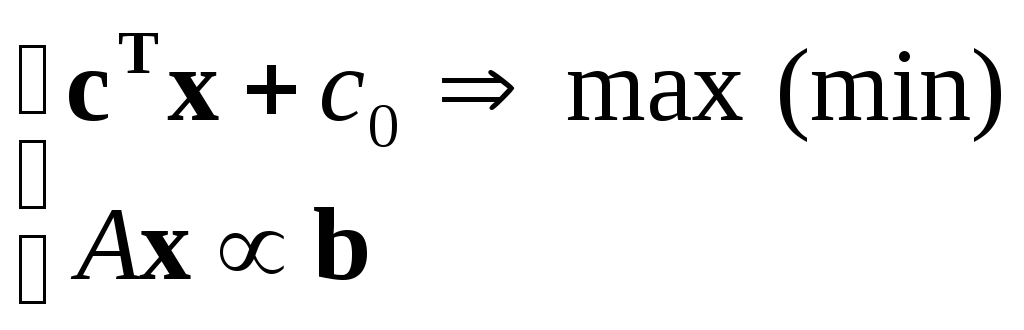

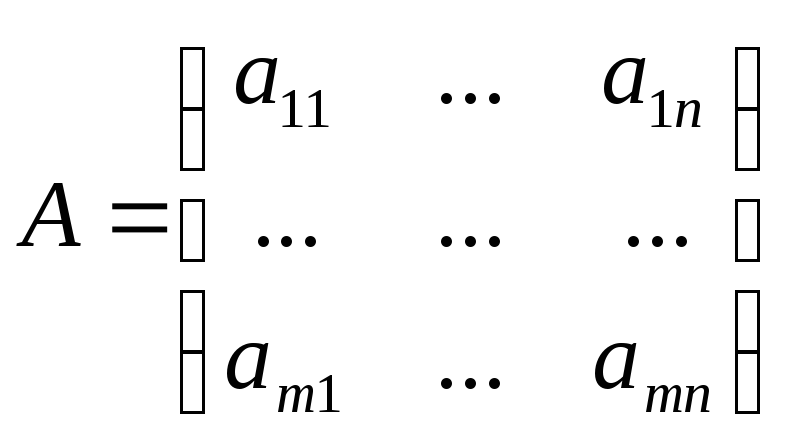
где - матрица размера, а- вектор условий (равенств и/или неравенств).

Задачи линейного программирования можно бы было считать разновидностью задач нелинейного программирования, если из определения задачи нелинейного программирования исключить слова о том, что хотя бы одна из фигурирующих в ее формулировке функций нелинейна. Нетрудно видеть, что ни в одной из приведенных в разделе 3.4 теорем данное ограничение не фигурировало. Поэтому все результаты, относящиеся к задачам нелинейного программирования, справедливы и для задач линейного программирования.

Как уже упоминалось, задачи нелинейного программирования выделены в отдельный класс, потому что для них разработаны методы, позволяющие успешно решать практически все задачи данного класса.

Различают три основные формы представления (вида) задач линейного программирования:

Стандартный вид задачи на максимум:

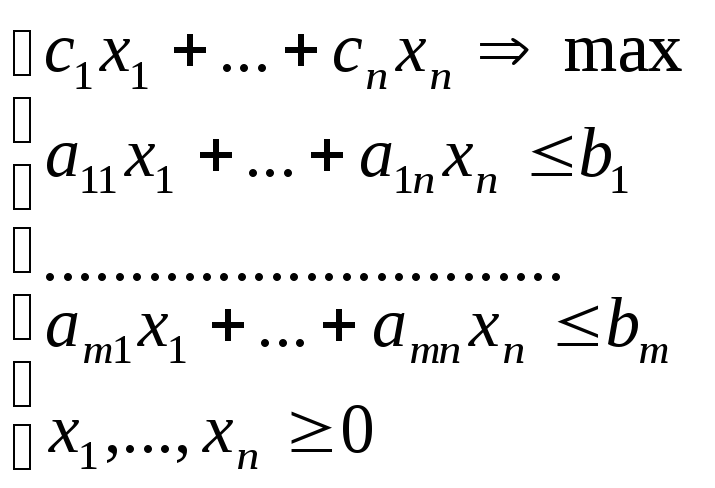, или, в векторной форме: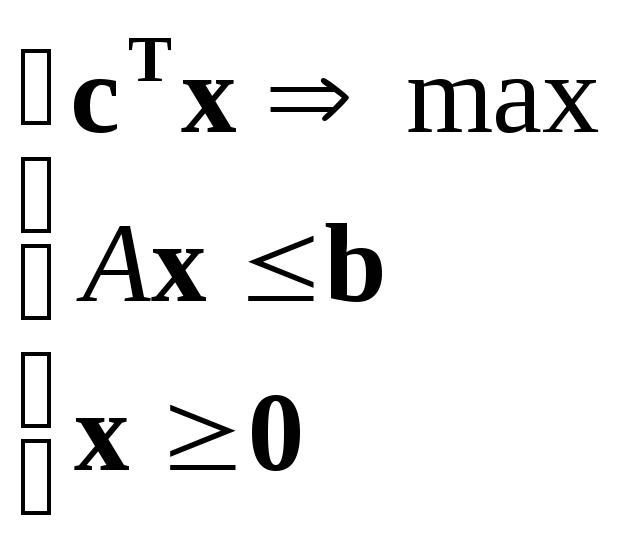, (4.1)

где ,,,.

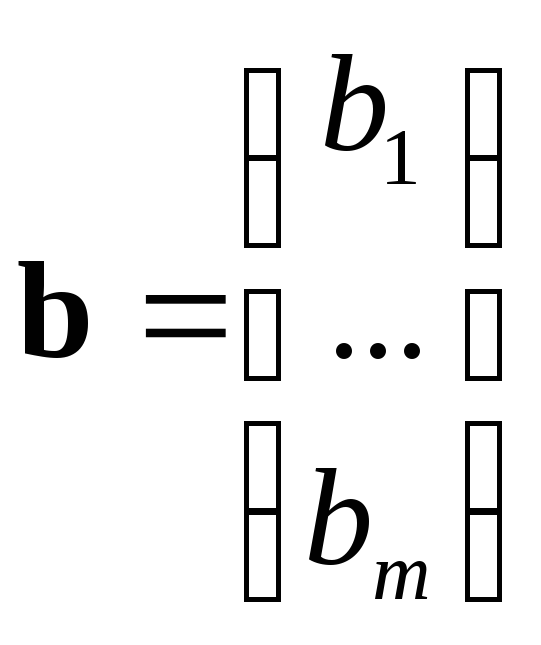Стандартный вид задачи на минимум:

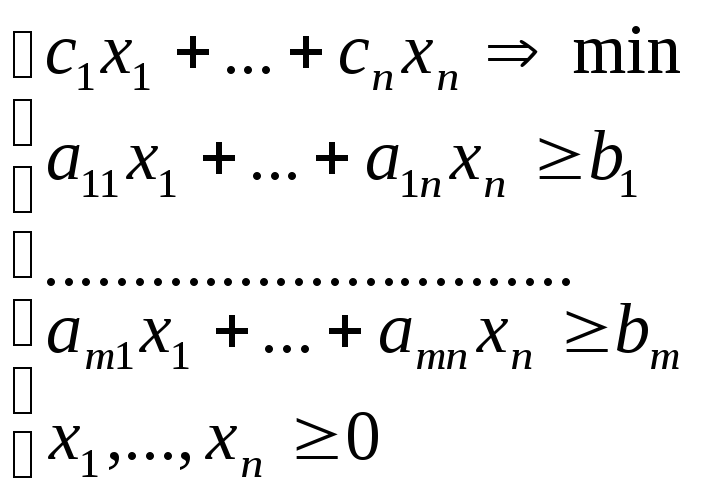, или, в векторной форме: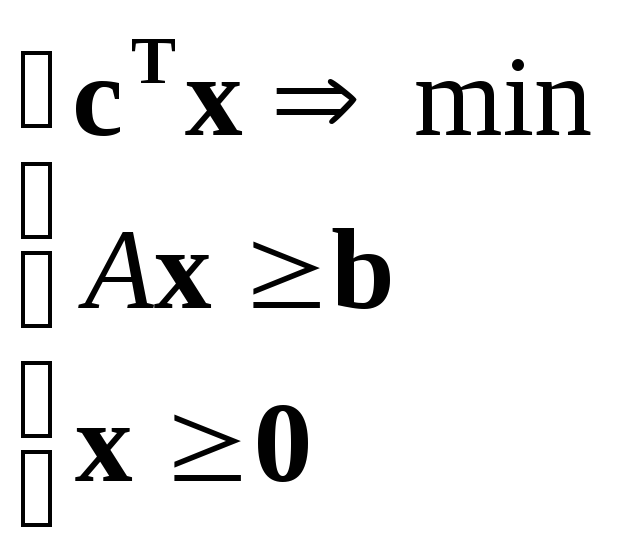. (4.2)

Канонический вид задачи:

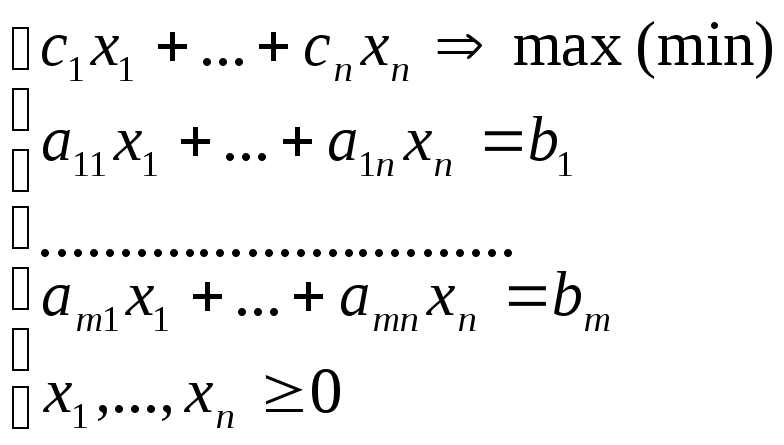, или, в векторной форме: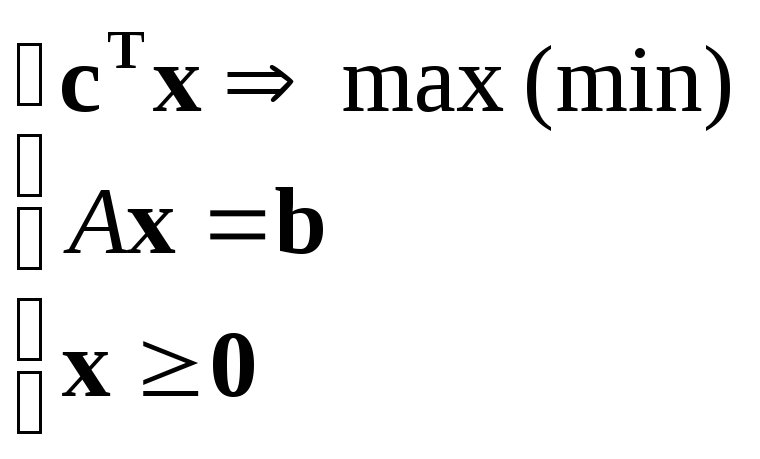. (4.3)

Отметим, что любая задача линейного программирования может быть представлена в любомиз видов (4.1) – (4.3).

Действительно, пусть какое-либо из ограничений имеет вид неравенства . Если его нужно представит в виде неравенства с противоположным знаком, достаточно умножить левую и правую части на "-1":. Если нужно иметь все ограничения в виде равенств, то к левой части неравенствадостаточно прибавить некоторую неотрицательную переменную, так называемую невязку, уравнивающую левую и правую части:При этом размерность задачи увеличится на единицу.

Для неравенств вида манипуляции аналогичны (в частности, для превращения его в равенство невязка вычитается).

Если исходное ограничение представлено в виде равенства , то его можно представить в виде системы двух неравенств, или.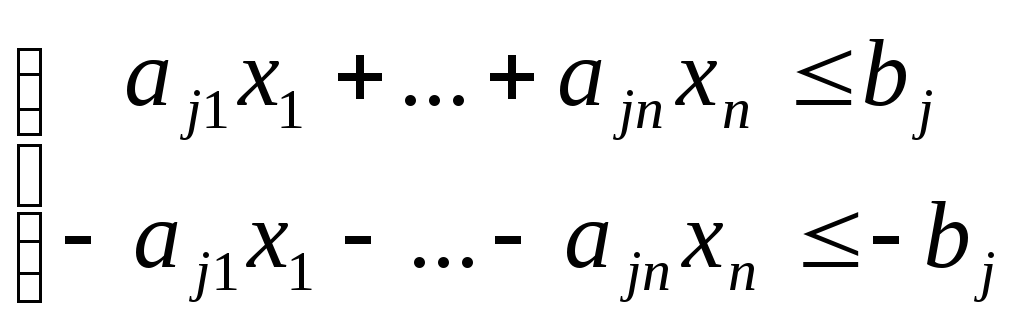

Если для некоторой переменной нет ограничения неотрицательности, то эту переменную можно представить в виде разности двух неотрицательных переменных:, после чего это выражение для переменнойподставляется в целевую функцию и во все ограничения.

Если в задаче требуется максимизировать целевую функцию: , то умножением ее на "-1" можно свести данную задачу к задаче на минимум:, и наоборот.

4.2. Структура допустимого множества и типы решений

Каждое функциональное ограничение вида илипредставляет собой замкнутое полупространство размерностиn, а ограничение видагиперплоскость вn-мерном пространстве. Прямые ограничениятакже образуют замкнутые полупространства. Допустимое множество задачи нелинейного программирования задается системой ограничений описанного вида, т.е. представляет собой пересечение замкнутых полупространств и/или гиперплоскостей. Такое образование носит название многогранного множества.

Многогранное множество описанного вида всегда замкнуто и выпукло, однако, в частном случае, может быть пустым или неограниченным; может иметь размерность nили меньшеn. Ниже приводятся примеры различных случаев дляn = 2.